A KöMaL 2011. januári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2011. február 10-én LEJÁRT. |
I. 256. Sok természeti jelenségnél megfigyelhetők a mintázatok. Ezek általában visszavezethetők olyan folyamatokra, melyeknél a kezdetben egységes rendszerben különböző alakzatok jelennek meg. Például kémiai hullámok haladnak az oldatban, vagy az állatok bőre foltossá válik.

Készítsünk programot i256 néven, amely a foltképződést a következő modellel szimulálja. Legyen egy M×M (10 M
M 500) négyzet, amelynek minden pontja két különböző színű állapotban lehet. Érdemes a pontok színét egy mátrixban tárolni.
500) négyzet, amelynek minden pontja két különböző színű állapotban lehet. Érdemes a pontok színét egy mátrixban tárolni.
A szimuláció indításakor minden pont színe véletlenszerűen a kettő közül az egyik. A továbbiakban minden lépésnél a négyzet egy véletlen pontjának a színét változtathatjuk meg. A szabály az, hogy minden pont alakuljon olyan színűvé, amilyen szomszédból több van. A változást a képernyőn jelenítjük meg anélkül, hogy a teljes négyzetet (reakcióteret) újrarajzolnánk. Ezzel a lassú képváltást, villódzást elkerülhetjük. A foltok mérete és alakja függ K (1 K
K 4) szomszédszám nagyságától.
4) szomszédszám nagyságától.
Minta K=1, 2 illetve 3 szomszédszámra:
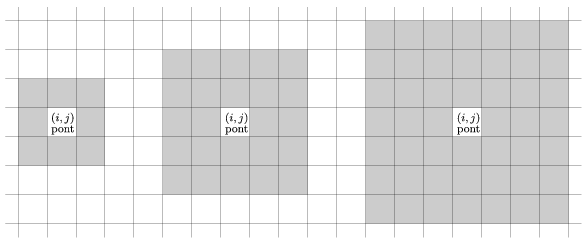
A reakciótér szélén természetesen a figyelembeveendő pontok száma kevesebb. A szimuláció addig tartson, ameddig a felhasználó le nem állítja.
A program parancssori argumentuma legyen M és K értéke.
Lehetséges eredmény M=150 és K=1 esetén
 |  |
| Feltöltött reakciótér | Szimuláció eredménye |
Beküldendő a program forráskódja (i256.pas, i256.cpp, ...), valamint a program rövid dokumentációja (i256.txt, i256.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 257. Egy áruház vezetése elemezni szeretné a vásárlási szokásokat. Az áruház kétemeletes és egy lépcsőházzal rendelkezik, amelyben az emeletek között egy felfelé és egy lefelé közlekedő mozgólépcső van. Optikai mérésadatgyűjtő rendszerrel számolják az áruház földszintjére belépő, illetve távozó, valamint az emeletekre felmenő és lemenő vásárlókat. Negyedóránként összesítik az adatokat a reggeli nyitástól az esti zárásig, azaz 8:00--20:00 óra között.
Honlapunkról letölthető a hat videokamerával negyedóránként összegzett vásárlószám a szamlalas.txt fájlban (tabulátorokkal tagolt, UTF-8 kódolású szövegállomány).
A megoldás során vegyük figyelembe a következőket:
- törekedjünk képlet, függvény, hivatkozás használatára;
- szükség esetén az R oszloptól jobbra végezzünk segédszámításokat.
1. Nyissuk meg táblázatkezelő program segítségével a szamlalas.txt fájlt úgy, hogy az első beolvasott adat az A1-es cellába kerüljön. A táblát mentsük a táblázatkezelő saját formátumában i257 néven.
2. Az A oszlopban hozzuk létre a mintának megfelelő időpontokat nyitástól zárásig.
3. A H, az I és a J oszlop celláiban adjuk meg, hogy hány vásárló volt az adott negyedóra végén az egyes szinteken, illetve a K oszlopban összesen az áruházban.
4. A vásárlószámlálás eredményeiből végezzünk elemzést az alábbiak alapján:
a. Az N2:P2 cellákban számítsuk ki, hogy a teljes nap összes adatát figyelembe véve hányan jártak az egyes szinteken.b. Írjuk ki az N3:P3 tartományban, hogy a vásárlók hány százaléka fordult meg az egyes szinteken. Az eredményeket nulla tizedes jegyes formátummal jelenítsük meg.
c. Határozzuk meg az N4:P4 cellákban, hogy hányan voltak a legtöbben egyszerre az egyes szinteken.
d. Az N5:P5 cellákban írjuk ki, hogy mikor voltak a legtöbben az adott szinten.
5. A számított értékeket tartalmazó cellákban alkalmazzunk kék betűszínt.
6. Az első sor celláit formázzuk a mintának megfelelően. Az oszlopok szélességét állítsuk úgy, hogy minden adat látszódjon.
7. Készítsünk oszlopdiagramot a munkalapra, mely megmutatja, hogy negyedóránként hányan voltak összesen az áruházban:
- a diagramon ne legyen jelmagyarázat;- a cím legyen ,,Összesen'';
- minden második negyedóra látszódjon a vízszintes tengelyen.
Minta:
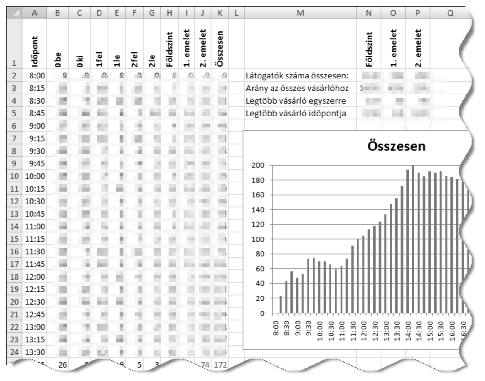
Beküldendő a táblázatkezelő munkafüzet (i257.xls, i257.ods, ...), illetve egy rövid dokumentáció (i257.txt, i257.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
I. 258. Az ókori görögök elképzelése szerint a kozmosz középpontjában a Föld foglalt helyet, a Hold, a Nap és a ,,többi'' bolygó körülötte keringett, az ég csillagai pedig egyhelyben álltak. Úgy gondolták, hogy a mozgó égitestek pályája csak tökéletes alakzat, ebben az esetben kör lehet. Azonban a legtöbb bolygó esetén megfigyelhető volt, hogy azok mozgása az égbolt állócsillagaihoz képest nem egyenletes, sőt egyes időszakokban visszafelé haladó. Ezért úgy gondolták, hogy az ilyen bolygók mozgása több kör segítségével írható le: a legegyszerűbb esetben egy Föld középpontú körön (deferens) halad egyenletesen egy másik kör (epiciklus) középpontja, és ezen második kör kerületén mozog egyenletesen a bolygó. Az alábbi ábra ezt az elképzelést szemlélteti:
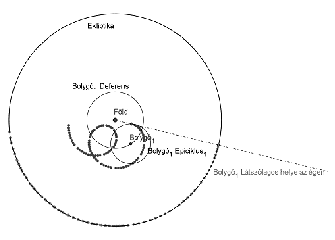
Mivel egyes bolygók valódi mozgása a mérések szerint eltért a fenti elképzeléstől, ezért további epiciklus köröket vezettek be úgy, hogy mindegyik ilyen kör középpontja az előző kerületén haladt, s a legutolsó epicikluson maga a bolygó. Több különböző sugarú és azok kerületén különböző periódusidővel haladó középpont, vagyis epiciklusok rendszerével a kor mérési lehetőségeinek pontosságát figyelembe véve helyesen kapták a bolygók mozgását.
Készítsük el két bolygó mozgásának szemléltetését a példához hasonló módon a GeoGebra (internetről ingyenesen letölthető a http://www.geogebra.org címről) számítógépes program segítségével. Mindkét bolygó esetében két epiciklus kör legyen, melyek sugara csúszka segítségével módosítható. Az egyes középpontok és a bolygók periódusideje szintén legyen csúszkával változtatható, valamint az idő múlását is így érjük el. A két bolygó valódi és látszólagos mozgását rajzoljuk ki nyomvonallal. A rajzlapon a szükséges segédpontokat és vonalakat rejtsük el, a fontos és lényeges elemeket színekkel is emeljük ki, és kapjanak érthető feliratot, tehát a kész munka legyen bemutatásra alkalmas, könnyen érthető.
Beküldendő a feladat megoldását adó i258.ggb GeoGebra állomány.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2011. február 10-én LEJÁRT. |
S. 59. Egy befektető Manhattan szívében új luxus bevásárlóközpont építését tervezi. Jól tudja, hogy a legnagyobb látogatottság úgy érhető el, ha a helyszín minél közelebb esik a lehetséges vásárlókhoz.
Ezért részletesen felmérte, hogy a város mely részéből hány vásárlóra lehet számítani, most pedig -- mint legjobb tanácsadóját -- minket kért meg, hogy javasoljunk számára olyan helyszínt, melynek eléréséhez átlagosan a lehető legkevesebbet kell utazniuk a vásárlóknak.
Írjunk programot a feladat megoldására. A megoldás során a hagyományokhoz hűen Manhattan úthálózatát tekintsük egy (kétirányú utakból álló) szabályos rácsnak, melynek kereszteződései az egész koordinátájú pontokban vannak.
Az egyszerűség kedvéért azonosítsuk a hozzájuk legközelebb eső kereszteződéssel mind a bevásárlóközpont, mind a vásárlók lakásainak helyét, a ,
koordinátájú kereszteződések távolsága pedig rács menti legkisebb távolságuk, azaz a következő legyen:
A program a felmérés eredményét a standard bemenetről olvassa. Ennek első sora a felmért kereszteződések számát tartalmazza, az ezt követő N darab sora pedig egy-egy kereszteződést ír le. Az i+1-edik sorban egy-egy szóközzel elválasztva három egész szám, az i-edik kereszteződés
koordinátái, illetve az onnan várható vásárlók 1
 wi
wi 1000 száma található.
1000 száma található.
A fenti jelölésekkel tehát a bevásárlóközpont számára azt az optimális kereszteződést keressük, melytől a felmért kereszteződések -- az egy kereszteződésben lakók számával súlyozott -- átlagos távolsága minimális:
A standard kimenet egyetlen sorába mindössze három, szóközzel elválasztott szám kerüljön: a bevásárlóközpont optimális helyszínének x0, y0 koordinátái, illetve az ehhez tartozó
átlagos távolság, 4 tizedes pontossággal. Több megoldás esetén bármelyik megadható.
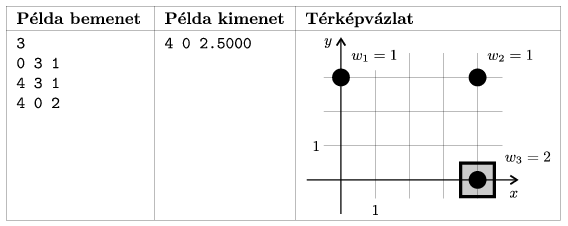
Értékelés: a maximális 8 pont eléréséhez a programnak a legnagyobb teszteseteket is egy percen belül meg kell oldania, ugyanakkor már 5 pont szerezhető az N 1000 feltételnek eleget tevő tesztesetek megoldásával is. További 2 pontot ér a dokumentáció.
1000 feltételnek eleget tevő tesztesetek megoldásával is. További 2 pontot ér a dokumentáció.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció (s59.txt, s59.pdf, ...) egy tömörített mappában (s59.zip).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

