KöMaL Problems in Informatics, March 2011
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on April 11, 2011. |
I. 262. A classical way of encrypting texts is the method of letter substitution, in which certain letters of the alphabet are systematically replaced by different ones. However, this encryption scheme (also called substitution cipher) was relatively easy to decipher -- even before the advent of computers -- using statistical methods by comparing the frequencies of different letters in the encrypted text and in the given language.
The file titkos.txt contains the encrypted text, encoded by using a letter substitution scheme. Before the encryption however the original text (in Hungarian) was preprocessed as follows:
[--] the diacritical marks were removed from vowels;
[--] each space was replaced by a letter q;
[--] all punctuation marks and indentation were removed;
[--] each letter was capitalized.
After these steps, the fixed substitution scheme was applied: each letter was replaced by another one.
You can find the beginning of the encrypted text below.

Your program i262 should decrypt the encoded text.
The first command line argument to your program is the name of the file containing the encrypted text. The second argument is the name of a file containing a long sample text in Hungarian. By using this second file, you should determine the relative occurrences of the letters (that is, their frequency distribution) in a typical Hungarian text. Sample texts of this type are found in the Hungarian Electronic Library for example. The third command line argument to your program is the name of the output file containing the decoded (or partially decoded) original text.
Your program should display the frequency distribution of the letters of the first two files. (Higher frequencies should come first.) The first 100-200 characters of the encrypted text should also be displayed, in which one should be able to perform some letter substitutions: the already substituted letters can be displayed as lowercase letters. It is not required to replace all the uppercase characters, additional corrections of the text may be performed afterwards.
You should submit the following in a compressed file (i262.zip, i262.rar):
[--] the decrypted text (megfejtes.txt),
[--] the source code of your program (i262.pas, i262.cpp, ...),
[--] a short documentation of your program (i262.txt, i262.pdf, ...) containing how to use your program, a brief description of your solution and specifying which developer environment to use for compiling the source code.
(10 pont)
solution (in Hungarian), statistics
I. 263. In Hungary the highest state award is the Kossuth prize. This was the topic of the database management task of the Hungarian matriculation exam in informatics in English in May 2010.
The files szemely.txt, foglalkozas.txt and mikor.txt contain data of the recipients of this prize between 1948 and 2010. (Here the words ``szemely'', ``foglalkozas'' and ``mikor'' refer to the person, the profession and the date, respectively.)
1. Create a new database named i263. Import the data tables into the database with names szemely, foglalkozas and mikor. The .txt files are UTF-8 encoded tabulator separated files and the field names are contained in the first lines.
2. After importing, the appropriate data formats and keys should be set:
Tables:

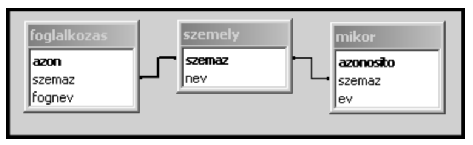
You should solve the following tasks. When a query is answered, no other data only the requested results should appear. Queries should be saved as indicated in the parentheses.
3. List the names and the year of reception of actors and performers. (The list should be sorted into descending order according to the year.) (3szin)
4. By using a query, list in alphabetical order the names having at least 4 professions. (4fogl)
5. By using a query, list the names and the year of receiving the prize of people having the same profession as Kozma László. Kozma László himself should not appear in this list. (5kozma)
6. What is the profession of those having received the Kossuth prize at least 3 times? Each profession should appear only once in this list. (6tobbszor)
7. By using a query, determine the professions receiving the most prizes in the year when the most prizes were awarded. (7legtobb)
8. List those professions existing in 1950 or before among the recipients, but not after this year. Each profession should appear only once in this list. (8nincs)
9. List each person whose profession names (more than one) contain the word ``szín''. Each person should appear only once in the result. (9szintobb)
Your database (i263.odb, i263.mdb, ...) together with a short documentation (i263.txt, i263.pdf) - also describing the name and version number of the database application - should be submitted in a compressed file i263.zip.
(10 pont)
solution (in Hungarian), statistics
I. 264. According to the ``rounding lemma'', for every matrix with real entries but all row sums and column sums integers, there exists a matrix with integer entries having the same row sums and column sums as the original one, moreover, each element of this integer matrix is the lower or upper integer part of the corresponding element of the original real matrix.
The proof of the rounding lemma is quite straightforward and also gives an algorithm how to construct the integer matrix.
If the original matrix has only integer entries, then we are done. Otherwise pick a non-integer element. Since the row sums are integers, there exists another non-integer number in the same row. But column sums are also integers, so the column of this second element must contain a third non-integer, whose row contains a fourth non-integer, and so on.
By alternately selecting rows and columns and marking the corresponding non-integer elements, sooner or later we have to visit a row or column that has already been selected. In this row or column there are exactly two matrix elements marked in an earlier stage, the element marked first is denoted by \(\displaystyle x\), while the element marked second is denoted by \(\displaystyle z\). Of course, there is a third element in this row or column, denoted by \(\displaystyle p\), which has been marked last, due to which we revisited the actual row or column. (In may happen that \(\displaystyle p=x\).)
Let us consider now the walk of this graph after we found \(\displaystyle p\). This walk begins with \(\displaystyle z\) and ends in \(\displaystyle p\), see the example. It is easily seen that the length of this walk is even, and contains exactly two marked matrix elements successively of each affected row or column. Therefore we can alternately add and subtract a constant \(\displaystyle \delta\) from the successive elements of this walk without changing any of the row or column sums.
Example. Suppose we start from the top left corner and visit non-integer elements in the order \(\displaystyle a_{11}\), \(\displaystyle a_{14}\), \(\displaystyle a_{34}\), \(\displaystyle a_{32}\), \(\displaystyle a_{12}\). After the \(\displaystyle 4^{\rm th}\) step (\(\displaystyle p =a_{12}\)) we reach a row already visited earlier (\(\displaystyle x=a_{11}\), \(\displaystyle z=a_{14}\)). The walk described in the above paragraph is therefore \(\displaystyle a_{14}\), \(\displaystyle a_{34}\), \(\displaystyle a_{32}\), \(\displaystyle a_{12}\).
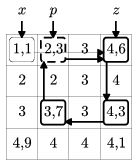
This constant \(\displaystyle \delta\) is defined to be the minimal (signed) distance between the marked matrix elements and the corresponding nearest integers. Then no ``overflow'' can occur when \(\displaystyle \delta\) is added or subtracted: each affected matrix element is changed at most to its lower or upper integer part and the number of non-integer elements is decreased by at least one.
Finally, the whole procedure is repeated if there are still non-integer elements in the matrix.
You should create a spreadsheet to perform a single iteration step of the above algorithm. The input and output matrix, further the constant \(\displaystyle \delta\) should be displayed similarly to our figure. (In the example, ``Bemenet'' is the input, ``Kimenet'' is the output, while ``Delta értéke'' is the value of \(\displaystyle \delta\).) Your sheet should be able to handle matrices of size at least \(\displaystyle 10\times 10\). Marked matrix elements should be displayed by using conditional formatting in both matrices. You can display an arbitrary solution if there is more than one.
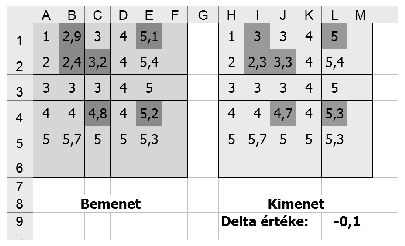
The task should be solved by using spreadsheet functions and without any macros. Auxiliary computations should be described in detail.
The spreadsheet (i264.xls, i264.ods, ...) together with a short documentation (i264.txt, i264.pdf, ...) describing your solution and the name and version number of the spreadsheet application should be submitted.
(10 pont)
 |
Problems with sign 'S'Deadline expired on April 11, 2011. |
S. 61. In a typical alphanumeric problem digits are represented by letters: each letter represents a digit, the same letters denote the same digit, and different ones a different digit. One should find a possible value for these letters such that the resulting addition is a valid one, with the further restriction that the leading digit of the sum can not be 0.
For example, consider the alphanumeric problem \(\displaystyle \overline{emmsk} + \overline{massk} = \overline{eemee\vphantom{k}}\). Then there is a solution (and the solution is unique in this case): \(\displaystyle a=7\), \(\displaystyle e=8\), \(\displaystyle k=4\), \(\displaystyle m=0\), \(\displaystyle s=9\), because after substitution we get the following equality: \(\displaystyle 80094 + 07994 = 88088\).
You should write a program that reads an alphanumeric problem in a given base from the standard input, then gives a possible solution (if it exists) and the number of all solutions.
The structure of the input is the following: the first line contains the base of the number system (\(\displaystyle 2 \le b \le 23\), represented as a decimal number), the second and third lines contain the two addends, while the fourth line contains the sum. The last three lines contain only lowercase letters of the English alphabet and their length is at most 1000 characters.
The first line of the standard output should contain the number of solutions. If this is greater than zero, then the second line should contain an arbitrary solution in the format specified below. Each letter should be listed, separated by a space, together with an equation sign and the corresponding digit value. Digits with value greater than 9 are represented by successive uppercase letters of the English alphabet, similarly to the hexadecimal number system.
In the example, ``Példa bemenet'' is the input, while ``Példa kimenet'' is a possible output.

We remark that the complete solution set of this example is the following:
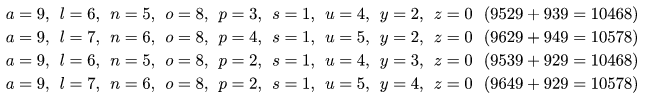
The time limit for your program is 1 minute in each test case.
The source code and project files of your solution (without the .exe file or any other auxiliary files generated by the compiler) should be submitted together with a short documentation in a compressed folder s61.zip.
You can obtain 8 points for this exercise if your program gives a correct answer to all test cases available on our web page, within the specified time limit. You may get a reduced number of points if your program does not give the number of solutions, or only able to work in the decimal system.
A further 2 points can be awarded for the documentation.
Downloadable files: s61.zip
(10 pont)
$Var(Body)
Upload your solutions above
