A KöMaL 2011. márciusi informatika feladatai

I-jelű feladatok A beküldési határidő 2011. április 11-én LEJÁRT.

---

I. 262. Szövegek titkosításának régen használt módszere a betűcsere, amelynél egy meghatározott rendszer szerint az ábécé egyes betűit egy másikra cserélik. Ezt már a számítógépek használata előtt is aránylag könnyen feltörték statisztikai módszerekkel, az egyes betűk előfordulási arányait figyelve az adott nyelvben és a kódolt szövegben.

Rendelkezésünkre áll a titkos.txt állományban egy betűcserés módszerrel titkosított szöveg. A szöveget a betűcserék előtt még át is kódolták.

Az átkódolás a következőképpen történt:

[--] Az ékezetes magánhangzók ékezet nélküli párjukkal lettek helyettesítve.

[--] A szóközöket q betűvel helyettesítették.

[--] A szövegből elhagyták az írásjeleket és minden más szövegtagolást.

[--] A teljes szövegben nagybetűs írásmódot állítottak be.

Ezek után végül minden betű helyére pontosan egy-egy másik került, végig azonos szisztéma szerint.

A szöveg kezdőrészlete:

Készítsünk programot i262 néven, amely segít megfejteni a titkosított szöveget.

A program első parancssori argumentuma legyen a megfejtendő titkos szöveget tartalmazó állomány neve, második argumentumaként pedig egy hosszú, magyar nyelvű szöveget tartalmazó állomány nevét lehessen megadni. Az állományból a magyar nyelvű szövegre jellemző betű-előfordulási arányokat határozzuk meg, ennek alapján próbálkozhatunk a titkos szöveg karakterhelyettesítésnek megfejtésével. Ilyen állományokat például a Magyar Elektronikus Könyvtárban találhatunk. A harmadik argumentum az általunk (legalábbis részben) visszakódolt szöveg kimeneti állományának neve legyen.

A program készítse el az első két állomány betűstatisztikáját és ezt jelenítse meg a képernyőn az előfordulás gyakorisága szerint csökkenően. A megfejtendő szöveg első 100-200 karakterét is jelenítse meg, és ezen lehessen karaktercserét végrehajtani. A már lecserélt karaktereket lehet kisbetűs írásmóddal megjeleníteni. Nem szükséges a programmal az összes nagybetűs karaktert egyszerre lecserélni, megengedett a szövegállomány utólagos javítása.

Beküldendő egy tömörített állományban (i262.zip, i262.rar):

[--] a megfejtett szöveg (megfejtes.txt),

[--] a program forráskódja (i262.pas, i262.cpp, ...),

[--] a program rövid dokumentációja (i262.txt, i262.pdf, ...), amely tartalmazza a program használatának bemutatását, a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

megoldás, statisztika

---

I. 263. A legmagasabb állami kitüntetés Magyarországon a Kossuth-díj. Ez volt a témája a 2010. májusi idegen nyelvű informatika érettségi gyakorlati adatbáziskezelés-feladatának.

A foglalkozas.txt, mikor.txt, szemely.txt állományokban rendelkezésünkre állnak az 1948 és 2010 között díjazottak adatai.

[1.] Készítsünk új adatbázist i263 néven. Importáljuk az adattáblákat az adatbázisba szemely, foglalkozas és mikor néven. A .txt típusú adatállományok UTF-8 kódolásúak, tabulátorokkal tagoltak és az első soruk tartalmazza a mezőneveket.

[2.] Beolvasás után állítsuk be a megfelelő adatformátumokat és kulcsokat:

Tábla:

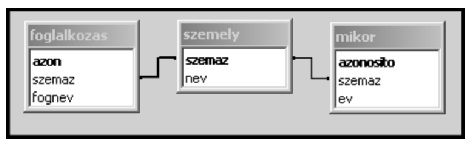
Készítsük el a következő feladatok megoldását. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. A megoldásainkat a zárójelben feltüntetett néven mentsük el.

[3.] Soroljuk fel a színészek, színművészek nevét és kitüntetésük évét az utóbbi szerint csökkenő sorrendben. (3szin)

[4.] Listázzuk ki lekérdezés segítségével ábécérendben azoknak a nevét, akiknél négy, illetve több foglalkozásnév van megadva. (4fogl)

[5.] Adjuk meg lekérdezés segítségével azoknak a nevét és díjazásának az évét, akik azonos foglalkozásúak, mint Kozma László. A listában Kozma Lászlót ne jelenítsük meg. (5kozma)

[6.] Milyen foglalkozásúak a kettőnél több Kossuth-díjjal elismertek? A listában minden foglalkozást csak egyszer jelenítsünk meg. (6tobbszor)

[7.] Lekérdezéssel határozzuk meg, hogy milyen foglalkozásúaknak adták a legtöbb díjat abban az évben, amikor a legtöbb díjazott volt. (7legtobb)

[8.] Listázzuk ki azokat a foglalkozásokat, amelyekkel 1950-ben és előtte a díjazottak rendelkeztek, de később ilyen mesterségű kitüntetett nem volt. A listában minden foglalkozás csak egyszer jelenjen meg. (8nincs)

[9.] Soroljuk fel azoknak a nevét, mindenkiét egyszer, akiknek több foglakozásnevében szerepel a ,,szín'' szó. (9szintobb)

Beküldendő az adatbázis (i263.odb, i263.mdb, ..., valamint egy rövid dokumentáció (i263.txt, i263.pdf) egy tömörített i263.zip állományban, amelyből kiderül az alkalmazott adatbázis-kezelő neve, verziószáma.

(10 pont)

megoldás, statisztika

---

I. 264. Az ún. kerekítési lemma kimondja, hogy bármely olyan valós elemű mátrixhoz, melynek minden sor- és oszlopösszege egész, létezik egy -- ugyanazokkal a sor- és oszlopösszegekkel rendelkező -- olyan mátrix is, melynek minden eleme is egész, sőt, minden eleme az eredeti mátrix megfelelő elemének alsó vagy felső egész része.

A lemma bizonyítása meglepően egyszerű, és algoritmust is ad az egész elemű mátrix elkészítésére.

Ha az eredeti mátrix csupa egész elemekből áll, akkor készen vagyunk, ellenkező esetben vegyük egy tetszőleges nem egész elemét. Mivel a sorösszegek egészek, ennek sorában biztosan van még egy nem egész elem, amelynek oszlopában pedig -- az egész oszlopösszegek miatt -- van egy harmadik, melynek sorában egy negyedik, és így tovább.

A nem egész elemeken ily módon -- azaz a sorok, illetve oszlopok mentén felváltva -- lépkedve, és közben a meglátogatott elemeket megjelölve, egyszer csak egy olyan sorba vagy oszlopba ütközünk, amelyben már jártunk. Ebben sétánk korábbi szakaszából pontosan két megjelölt mátrixelem lesz: egy, amelyen keresztül először megérkeztünk a kérdéses sorba vagy oszlopba (ezt jelölje x), és egy másik, amellyel elhagytuk azt (z). Ezen kívül van még természetesen a harmadik, ,,problémás'' mátrixelem (p), amelyen keresztül ismét megérkeztünk a korábban már látogatott sorba vagy oszlopba (ez esetleg egybeesik x-szel).

Tekintsük most a séta ütközés utáni részéből képzett körsétát, tehát azt, amely z-vel kezdődik és p-ben ér véget (lásd: példa). Könnyen látható, hogy ez a körséta páros hosszú, és minden érintett sorból és oszlopból pontosan 2 megjelölt mátrixelemet tartalmaz, mégpedig egymás után. Így amennyiben a körséta minden eleméhez felváltva hozzáadunk, illetve kivonunk egy  konstanst, a sor- és oszlopösszegek nem változnak.

Példa: Amennyiben a bal felső sarokból indulunk, és a nem egész mátrixelemeket az a₁₁, a₁₄, a₃₄, a₃₂, a₁₂ sorrendben kezdjük el meglátogatni, az 4. lépés után (p=a₁₂) jutunk először már meglátogatott sorba (x=a₁₁, z=a₁₄). A bejárás ütközés utáni szakaszából kapott körséta tehát: a₁₄, a₃₄, a₃₂, a₁₂.

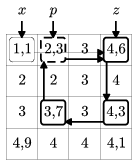
Ezt a konstanst válasszuk úgy, hogy a megjelölt mátrixelemek és a hozzájuk legközelebb eső egész számok közti különbségek abszolút értékeinek minimuma legyen (a megfelelő előjellel). Ekkor a hozzáadásokkor és kivonásokkor egyik mátrixelem sem ,,csordulhat túl'' a saját felső vagy alsó egész részén, és legalább eggyel csökken a nem egész elemek száma. Amennyiben pedig még ez után is marad nem egész elem, úgy az egész eljárást ismételjük meg.

Készítsünk táblázatot, mely a fenti algoritmus egyetlen iterációját hajtja végre: a bemeneti és kimeneti mátrix, illetve értéke az ábrán láthatóhoz hasonló módon helyezkedjen el (de a megoldásban legalább 10×10-es mátrixoknak biztosítsunk helyet!), a megjelölt mátrixelemeket mindkét mátrixban feltételes formázással emeljük ki. Több lehetséges megoldás esetén bármelyik megadható.

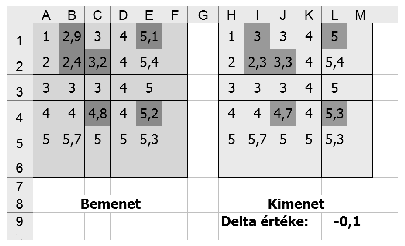
A feladatot táblázatkezelő függvényekkel, makrók használata nélkül kell megoldani, a mellékszámításokról részletes magyarázatot várunk.

Beküldendő a táblázatkezelő munkafüzet (i264.xls, i264.ods, ...), illetve egy rövid dokumentáció (i264.txt, i264.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma, valamint a megoldás leírása.

(10 pont)

megoldás, statisztika

S-jelű feladatok A beküldési határidő 2011. április 11-én LEJÁRT.

---

S. 61. Az ún. betűösszeadás-feladványokban számjegyek helyett betűk szerepelnek. Az azonos betűk ugyanazt a számjegyet jelentik, a különbözőek különbözőeket. A betűk jelentését úgy kell megválasztani, hogy érvényes összeadást kapjunk. További kikötés, hogy az összeg első számjegye nem lehet nulla.

Például: \(\displaystyle \overline{emmsk} + \overline{massk} = \overline{eemee\vphantom{k}}\). Ennek a betű-összeadásnak egyetlen megoldása van: \(\displaystyle a=7\), \(\displaystyle e=8\), \(\displaystyle k=4\), \(\displaystyle m=0\), \(\displaystyle s=9\). Behelyettesítve a következő összeadást kapjuk: \(\displaystyle 80094 + 07994 = 88088\).

Írjunk programot, amely a standard bemenetről beolvas egy megadott számrendszerbeli betűösszeadás-feladványt, és megad egy megoldást (ha létezik), valamint azt, hogy hány megoldása van.

A bemenet szerkezete a következő: az első sorban a számrendszer alapszáma (\(\displaystyle 2 \le b \le 23\)) szerepel (számmal írva), a másodikban és a harmadikban a két összeadandó, a negyedikben pedig az összeg (mindben csak az angol ábécé kisbetűi szerepelnek, és hosszuk legfeljebb 1000 karakter).

A standard kimenet első sorában a megoldások száma szerepeljen. Amennyiben ez nem nulla, úgy a második sorban adjunk is meg egy tetszőleges megoldást, az alábbi formátumban. A bemenetben szereplő minden betűt soroljunk fel (szóközökkel elválasztva), és egyenlőségjellel kapcsolva írjuk melléjük a hozzárendelt számjegyet. A 9-nél nagyobb értékű számjegyeket rendre az angol ábécé nagybetűivel jelöljük, a hexadecimális számrendszerhez hasonlóan.

A példa összes megoldása:

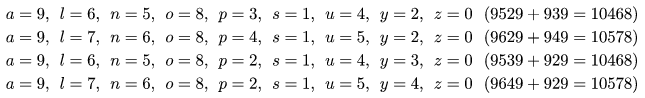
A futásidőlimit tesztesetenként 1 perc.

Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció egy tömörített s61.zip mappában.

Értékelés: 8 pontot ér az a program, amely a honlapunkon elérhető mindegyik tesztesetre a megadott időkorláton belül helyes eredményt ad. Részpontszámok kaphatóak az olyan programra, amely nem adja meg a megoldások számát, vagy csak 10-es számrendszerbeli számokra működik. További 2 pont szerezhető a dokumentációval.

Példa bemenetek és példa kimenetek: s61.zip

(10 pont)

megoldás, statisztika