A KöMaL 2011. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2011. november 10-én LEJÁRT. |
M. 317. A4-es írólapokból vágjunk ki különböző  középponti szögű, a=10 cm sugarú körcikkeket, majd óvatos hajtogatással és ragasztással formáljunk mindegyikből egy-egy egyenes körkúpot. Különböző
középponti szögű, a=10 cm sugarú körcikkeket, majd óvatos hajtogatással és ragasztással formáljunk mindegyikből egy-egy egyenes körkúpot. Különböző  félnyílásszögű kúpokat kapunk.
félnyílásszögű kúpokat kapunk.
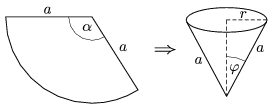
Mérjük meg, hogyan függ a nagy magasságból leejtett kúpok állandósult sebessége a  félnyílásszögtől!
félnyílásszögtől!
Varga István (1952--2007) feladata
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2011. november 10-én LEJÁRT. |
P. 4370. Egy repülőgép a 2 km-es útszakaszt állandó hátszéllel 15 másodperc, ugyanekkora ellenszéllel 20 másodperc alatt teszi meg.
Hány km/h a repülőgép sebessége, és mekkora a szélsebesség?
Tarján Imre fizikaverseny, Szolnok
(3 pont)
P. 4371. Egy csúzliból kilőtt kavics 50 m/s sebességgel indul el függőlegesen felfelé. Ha nem lenne légellenállás,
a) hol lenne a kavics 7 másodperc múlva;
b) mekkora lenne ekkor a sebessége;
c) mennyi utat tenne meg 7 másodperc alatt?
Közli: Simon Péter, Pécs
(3 pont)
P. 4372. Vízszintes asztalon két, egyenként 2 kg tömegű kiskocsi nyugszik egy vonalban. Az egyiken egy rugó is van az ábra szerint. A bal oldali kiskocsit sebességgel meglökjük, amely ezután a jobb oldali kiskocsinak ütközik.

Mennyi energia van a rugóban, amikor az az ütközés során a legrövidebb?
Közli: Holics László, Budapest
(3 pont)
P. 4373. Vízszintes, súrlódásmentes felületen lévő, m=0,5 kg tömegű testeket D=16 N/m direkciós erejű, L=20 cm hosszúságú, elhanyagolható tömegű, nyújtatlan rugó köt össze. A testeket egy adott pillanatban v0=0,36 m/s sebességgel elindítjuk a jobbra levő függőleges fal irányába. A jobb oldali test rugalmasan ütközik a fallal.
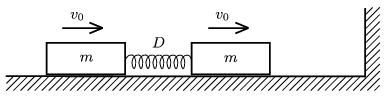
a) Mekkora a mozgás során a rugó maximális összenyomódása?
b) A fallal való ütközés után mennyi idő múlva lesznek egymáshoz legközelebb a testek?
c) Lesz-e további ütközés a fallal? Hogyan mozog a rendszer, ha elegendő ideig várunk?
d) Mekkora a rendszer lendületváltozása, miután valamennyi ütközés lezajlott?
Közli: Kotek László, Pécs
(4 pont)
P. 4374. Egy kertben kicsiny, gömb alakú locsolófejjel öntöznek, amelyből minden irányban azonos sebességgel áramlik ki a víz. A függőlegesen induló vízsugár a gömbtől számítva h magasságba jut. Egyik alkalommal a locsolófejet a földre helyezik, majd egy másik esetben h magasságba. Hányszor nagyobb területet tudnak megöntözni a második esetben? (A közegellenállást ne vegyük figyelembe; a szórófejben a víznyomást állandónak tekinthetjük.)
Közli: Kobzos Ferenc, Dunaújváros
(5 pont)
P. 4375. Állandó tömegű ideális gáz az ábrán látható körfolyamatot végzi. Ábrázoljuk ezt a körfolyamatot (p,V) helyett (p,T), illetve (E,V) diagramon! (E a gáz belső energiája.)
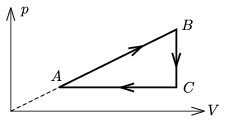
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4376. Egy C1=180 pF és egy C2=20 pF kapacitású, légszigetelésű síkkondenzátort sorbakapcsoltunk, és szabad végeiket egy állandó, U0=24 V elektromotoros erejű akkumulátorra kötöttük. Így mindegyik kondenzátorban tárolódott valamennyi energia. Később, a kapcsolásukon nem változtatva, megnöveltük a kondenzátorokban tárolt energiát, mindkettőben ugyanakkora értékkel. Ezt úgy oldottuk meg, hogy a C2 kapacitású kondenzátor lemezei közötti teret teljesen kitöltöttük 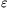 r relatív dielektromos állandójú üveggel, a C1 kapacitású kondenzátort változatlanul hagytuk.
r relatív dielektromos állandójú üveggel, a C1 kapacitású kondenzátort változatlanul hagytuk.
a) Mekkora volt a használt üveg 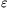 r relatív dielektromos állandója?
r relatív dielektromos állandója?
b) Mennyivel nőtt a kondenzátorok energiája?
(A levegő relatív dielektromos állandóját 1-nek vehetjük.)
Közli: Légrádi Imre, Sopron
(5 pont)
P. 4377. Egy veszteséges tekerccsel sorba kötünk egy 600 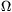 nagyságú, ohmos ellenállású fogyasztót. A tekercsen 200 V, a fogyasztón 100 V feszültséget mérünk. Mekkora a tekercs induktivitása és ohmos ellenállása, ha a hálózat effektív feszültsége 230 V, és frekvenciája 50 Hz?
nagyságú, ohmos ellenállású fogyasztót. A tekercsen 200 V, a fogyasztón 100 V feszültséget mérünk. Mekkora a tekercs induktivitása és ohmos ellenállása, ha a hálózat effektív feszültsége 230 V, és frekvenciája 50 Hz?
Tornyai Sándor fizikaverseny, Hódmezővásárhely
(4 pont)
P. 4378. Egy gyorsítóban valamely elektromos töltésű részecskét a fénysebesség 80 százalékára sikerült felgyorsítani. Mekkora lesz a sebessége, ha a további gyorsítás során a részecske mozgási energiája a kétszeresére nő?
Közli: Szombathy Miklós, Eger
(4 pont)
P. 4379. A rádium tömegszáma A=226, felezési ideje 1622 év. Mennyi az aktivitása 1 gramm rádiumnak? (Régebben ezen alapult az aktivitás egysége: 1 g rádium aktivitását nevezték 1 curie-nek.)
Marx György (1927--2002) feladata
(3 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

