A KöMaL 2011. októberi matematika feladatai

K-jelű feladatok A beküldési határidő 2011. november 10-én LEJÁRT.

---

K. 301. Egy dobozban piros és sárga golyók vannak. Ha kivennénk 1 piros golyót, akkor a bennmaradó golyók hetedrésze lenne piros. Ha ehelyett kivennénk 5 sárga golyót, akkor a bennmaradók hatodrésze lenne piros. Hány golyó van a dobozban?

(6 pont)

megoldás, statisztika

---

K. 302. Melyek azok a természetes számok, amelyek harmadik és negyedik hatványa együtt az összes számjegyet tartalmazza pontosan egyszer?

(6 pont)

megoldás, statisztika

---

K. 303. Hány darab háromszöget, rombuszt és húrtrapézt találhatunk az ábrán?

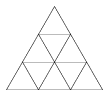
(6 pont)

megoldás, statisztika

---

K. 304. Az ABCD téglalap AB oldalának harmadolópontja X, CD oldalának harmadolópontja Y az ábrának megfelelően. Határozzuk meg, hogy az ábrán szürkével jelölt síkidom területe hányadrésze az ABCD téglalap területének.

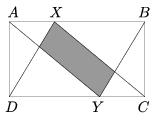
(6 pont)

megoldás, statisztika

---

K. 305. Amerika csapadékban szegény részeinek műholdas felvételét nézegetve érdekes köröket láthatunk (pl. Texasban, a 79068 ZIP-kódú területen, a Google Earth programban a kereséshez TX 79068-at írva.) A körök abból a sajátos öntözési technológiából származnak, melyben egy rúd alakú öntözőberendezés forog körben a középpontja vagy az egyik vége körül. Természetesen így a földterület egy része termelésre nem használható, mert a víz nem mindenütt éri el, csak a körökön belül.

Joe, Jim és Jack három testvér, mindhármójuknak 1 km oldalhosszúságú, négyzet alakú földjük van. Az öntözött területet az ábrán látható módon alakították ki:

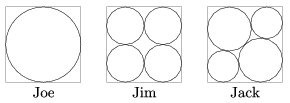
Jack elrendezésében a kisebbik körök sugara 210,5 m. Melyikük elrendezése a leghatékonyabb, azaz melyikük tudja földjének legnagyobb részét növénytermesztésre használni?

(6 pont)

megoldás, statisztika

---

K. 306. Töltsünk ki egy 4×4-es négyzetes táblázatot a 2011 számjegyeivel úgy, hogy minden sorban, minden oszlopban és a két átlóban is a 2, 0, 1, 1 álljon valamilyen sorrendben. Hány különböző, a feltételnek megfelelő kitöltés létezik?

(6 pont)

megoldás, statisztika

C-jelű feladatok A beküldési határidő 2011. november 10-én LEJÁRT.

---

C. 1090. Tizenhárom szabályos dobókockából összeragasztottuk a képen látható testet. Hány pötty lehet maximálisan a felületén?

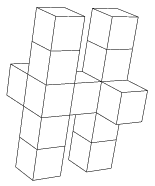
(5 pont)

megoldás, statisztika

---

C. 1091. Az ötöslottóban az egyik játékhéten a nyerőszámok emelkedő számsorrendben a következők: , , , , . Az öt szám összege , a harmadik és a második szám szorzata , a harmadik és az ötödik szorzata pedig . Határozzuk meg az a, b, c, d, e számjegyeket.

(5 pont)

megoldás, statisztika

---

C. 1092. Az AB szakasz belső pontja C. Szerkesszünk az AC és BC szakaszokra szabályos háromszögeket az AB egyik oldalán, majd szerkesszünk szabályos háromszöget az AB szakaszra a másik oldalán. Bizonyítsuk be, hogy a háromszögek súlypontjai egy szabályos háromszög csúcsai.

(5 pont)

megoldás, statisztika

---

C. 1093. Az f(x) függvény helyettesítési értéke tetszőleges x valós szám esetén legyen az x²-4x+3, az x-1 és a -x+7 értékek közül a legkisebb. Adjuk meg az f(x)=c egyenlet megoldásainak számát a c valós paramétertől függően.

(5 pont)

megoldás, statisztika

---

C. 1094. Az ABC egyenlőszárú derékszögű háromszögben a BC befogón a C-hez közelebbi negyedelőpont H, a CA befogón felvett G pontra CG:GA=3:2. Mekkora szöget zárnak be a HA és a GB szakaszok?

(5 pont)

megoldás, statisztika

B-jelű feladatok A beküldési határidő 2011. november 10-én LEJÁRT.

---

B. 4382. Jelöljön x egész számot. Mutassuk meg, hogy ha a

kifejezés értéke egész, akkor négyzetszám.

(3 pont)

megoldás, statisztika

---

B. 4383. Az ABCD konvex négyszög oldalaira teljesül, hogy AB>BC>CD>DA. Az ABD, illetve a BCD háromszögekbe írt kör a négyszög BD átlóját rendre az E és F pontban érinti. Hasonlóan az ABC, illetve az ACD háromszögbe írt kör az AC átlót rendre a H és G pontban érinti. Mutassuk meg, hogy EF=GH.

Javasolta: Miklós Szilárd (Herceghalom)

(3 pont)

megoldás, statisztika

---

B. 4384. Lapunk B. 4283. feladata szerint, ha egy 23×23-as négyzetet felbontunk 1×1-es, 2×2-es és 3×3-as négyzetekre, akkor ehhez szükségünk van legalább egy darab 1×1-es négyzetre is. Hol helyezkedhet el az 1×1-es négyzet, ha tudjuk, hogy pontosan egy szerepel a felbontásban?

Javasolta: Gyenes Zoltán (Budapest)

(5 pont)

megoldás, statisztika

---

B. 4385. Oldjuk meg az {x}={x²}={x³} egyenletrendszert (ahol {y} az y szám törtrészét jelöli).

(4 pont)

megoldás, statisztika

---

B. 4386. Van-e olyan racionális szám, amely 10-es számrendszerbeli alakjából a számjegyeinek egy részét elhagyva megkapjuk a -t?

(4 pont)

megoldás, statisztika

---

B. 4387. Az ABCDEF húrhatszögben AB=BC, CD=DE és EF=FA. Bizonyítsuk be, hogy a BDF háromszög területe fele a hatszög területének.

(4 pont)

megoldás, statisztika

---

B. 4388. Az ABC hegyesszögű háromszög AB oldalának belső pontja D. A D ponton keresztül az AC oldallal húzott párhuzamos a BC oldalt az E, a D-n keresztül a BC oldallal húzott párhuzamos pedig az AC oldalt az F pontban metszi. Az ADF és BDE körök második metszéspontja G. Igazoljuk, hogy ABEF akkor és csak akkor húrnégyszög, ha G rajta van a CD szakaszon.

Javasolta: Miklós Szilárd (Herceghalom)

(4 pont)

megoldás, statisztika

---

B. 4389. Egy egyenesen adott négy pont: A, B, C és D ebben a sorrendben. Tekintsük az összes olyan egymást érintő körpárt, amelyek közül az egyik átmegy az A és a B, a másik a C és a D pontokon. Határozzuk meg az érintési pontok mértani helyét.

(4 pont)

megoldás, statisztika

---

B. 4390. Hány megoldása van a  egyenletnek a [0,20] intervallumban?

(4 pont)

megoldás, statisztika

---

B. 4391. Egy ötszög magasságán egy csúcs szemközti oldaltól vett távolságát értjük. Legyen P olyan ötszög, amelynek minden szöge 108^o és minden magassága különböző. Mutassuk meg, hogy P csúcsait valamelyik irányban megszámozhatjuk sorban úgy, hogy a megfelelő magasságokra

m₁>m₃>m₄>m₅>m₂

teljesüljön.

Javasolta: Kevei Péter, Vígh Viktor (Szeged)

(5 pont)

megoldás, statisztika

A-jelű feladatok A beküldési határidő 2011. november 10-én LEJÁRT.

---

A. 542. Van 1000 pénzérménk, de tudjuk, hogy közülük 100 hamis. Ismerjük a valódi érmék súlyát, és tudjuk, hogy a hamis érmék könnyebbek, mint a valódiak, de a hamis érmék súlyai különbözők is lehetnek. Egy egykarú mérleggel szeretnénk találni egy hamis érmét. Minden lépésben megmérhetjük néhány érme súlyának összegét, ezzel megállapíthatjuk, hogy a mérlegre tett érmék között van-e hamis. Hány mérésre van szükségünk, hogy biztosan találjunk egy hamis érmét?

Javasolta: Pálvölgyi Dömötör (Budapest)

(5 pont)

megoldás, statisztika

---

A. 543. Néhány független esemény valószínűségének az összege 4. Bizonyítsuk be, hogy több, mint 1/2 eséllyel a bekövetkező események számának 4-gyel való osztási maradéka 0 vagy 3.

Javasolta: Csóka Endre (Budapest)

(5 pont)

megoldás, statisztika

---

A. 544. Adott az O középpontú k kör és rajta a különböző A, B, C, D rögzített pontok. A k' kör k-t merőlegesen metszi A-ban és B-ben. Vegyünk fel az OA egyenesen egy X változó pontot. Legyen U az ACX és a k' körök A-tól különböző metszéspontja, V az ADX és a k' körök A-tól különböző metszéspontja, W a BDU kör és az OB egyenes B-től különböző metszéspontja, végül legyen E a BVW és a k körök B-től különböző metszéspontja. Igazoljuk, hogy az E pont helyzete nem függ az X pont megválasztásától.

(5 pont)

megoldás, statisztika