KöMaL Problems in Mathematics, February 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 12, 2012. |
K. 325. Kate kept rolling a regular die until there was a number appearing the third time on top. This occurred on the 12th throw. The sum of the numbers rolled altogether in the 12 cases was 47. Which number was rolled three times? Which number was rolled the least number of times?
(6 pont)
solution (in Hungarian), statistics
K. 326. An interior designer is planning the illumination of a large lecture hall. He is using LEDs (light emitting diodes) arranged in concentric circles. The LEDs are uniformly spaced along each circle. The radius of each circle is the double of the previous circle. If lines are drawn from each lead of a circle through the centre, only every other line will have a LED on the next circle inside. a) Show that the separation of two consecutive LEDs on the same circle, as measured along the circle, is constant (that is, independent of the circle selected). b) Determine this distance (measured along the circle) if the radius of the largest circle is 20 metres, the number of circles is 8, and the 4th smallest circle contains 112 LEDs. c) What is the total number of LEDs used?
(6 pont)
solution (in Hungarian), statistics
K. 327. The sum of four positive integers is 125. If the first number is increased by 4, the second number is decreased by 4, the third number is multiplied by 4 and the fourth number is divided by 4, the results will be all equal. What may be the four original numbers?
(6 pont)
solution (in Hungarian), statistics
K. 328. 0, 1, 2, 3 are substituted for a, b, c, d in the expression ab+cd in all possible orders. What will be the sum of the resulting numbers?
(6 pont)
solution (in Hungarian), statistics
K. 329. Given that x is a positive real number such that , determine the value of
without finding the value of x.
(6 pont)
solution (in Hungarian), statistics
K. 330. A regular triangle ABF is inscribed in a square ABCD as shown in the figure. The length of AE is 2. What is the area of the square ABCD?
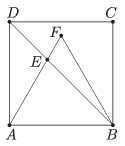
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 12, 2012. |
C. 1110. Andrew is going for a walk, starting from a corner of a block in a housing estate where streets form a rectangular lattice. During his walk, he only changes direction at street corners. The buildings form square blocks, 15 m on a side, and the width of the streets is negligible. Show that if Andrew ends his walk at the starting point, then the length of his path in metres will be an even number.
(5 pont)
solution (in Hungarian), statistics
C. 1111. The sum of all edges of two cubes is divisible by 72. Prove that the sum of their volumes is divisible by 6.
(5 pont)
solution (in Hungarian), statistics
C. 1112. The parallels drawn through a point P of side AB of a triangle ABC to the other two sides intersect the sides AC and BC at the points Q and R, respectively. For what position of the point P is the area of quadrilateral CQPR a maximum?
Suggested by G. Holló, Budapest
(5 pont)
solution (in Hungarian), statistics
C. 1113. P is the point in the interior of a rectangle ABCD for which the tangents of the angles  PAB,
PAB,  PBC,
PBC,  PCD and
PCD and  PDA are 1, 2,
PDA are 1, 2, and
, respectively. What is the tangent of the angle enclosed by the diagonals?
(5 pont)
solution (in Hungarian), statistics
C. 1114. Solve the equation log2log3x=log3log2x.
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 12, 2012. |
B. 4422. There are 99 sticks lying on a table, their lengths are 1,2,3,...,99 units. Andrea and Bill play the following game: they take turns removing one stick of their choice. Andrea starts the game. The game ends when there are exactly three sticks remaining on the table. If it is possible to make a triangle out of the three sticks then Andrea wins. Otherwise, Bill is the winner. Who has a winning strategy?
(5 pont)
solution (in Hungarian), statistics
B. 4423. Given the lines of the medians of a triangle and one point lying on a side, construct the triangle.
Suggested by J. Pataki, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 4424. Velo City Transportation Company are planning to operate a bus service along a ``uniformly populated'' straight road of length  . How should the n bus stops be positioned along the road, so that the customers need to walk as little as possible?
. How should the n bus stops be positioned along the road, so that the customers need to walk as little as possible?
(4 pont)
solution (in Hungarian), statistics
B. 4425. Solve the equation .
(3 pont)
solution (in Hungarian), statistics
B. 4426. In a tetrahedron ABCD, opposite edges are perpendicular, and face BCD is an acute-angled triangle. The foot of the altitude from vertex A is T. Find the shortest path AT on the surface of the tetrahedron.
(4 pont)
solution (in Hungarian), statistics
B. 4427. Show that if  ,
,  and
and 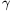 are the angles of a triangle then (sin
are the angles of a triangle then (sin  +sin
+sin  +sin
+sin 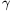 )2>9sin
)2>9sin  sin
sin  sin
sin 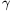 .
.
(3 pont)
solution (in Hungarian), statistics
B. 4428. A triangle is inscribed in a unit circle. What may be the distance between the centres of two escribed circles of the triangle?
(4 pont)
solution (in Hungarian), statistics
B. 4429. A1B1C1 and A2B2C2 are two triangles such that their sides A1B1 and A2B2, B1C1 and B2C2, as well as A1C1 and A2C2 are parallel. Vertex A1 is connected to vertices B2 and C2, vertex B1 is connected to C2 and A2, and vertex C1 is connected to A2 and B2. Given that the areas of the original triangles are T1 and T2, what may be the area of the hexagon formed by the midpoints of the connecting line segments obtained in this way?
(4 pont)
solution (in Hungarian), statistics
B. 4430. We play the following game of tossing a coin: We make a bet before each toss. The bet may be at most as large as all the money we have. Then we make a guess on the result. If our guess is right, we will receive the double of the bet, otherwise we will lose it. Determine those values of k>1 for which there exists an integer n with a strategy such that the probability of receiving k times our initial amount of money in at most n games is at least .
(5 pont)
solution (in Hungarian), statistics
B. 4431. Are there positive integers n and k such that ?
(5 pont)
 |
Problems with sign 'A'Deadline expired on March 12, 2012. |
A. 554. The circumcenter of the cyclic quadrilateral ABCD is O. The second intersection point of the circles ABO and CDO, other than O, is P, which lies in the interior of the triangle DAO. Choose a point Q on the extension of OP beyond P, and a point R on the extension of OP beyond O. Prove that  QAP=
QAP= OBR holds if and only if
OBR holds if and only if  PDQ=
PDQ= RCO.
RCO.
(5 pont)
A. 555. The points of an n×n×n rectangular grid are colored with n colors in such a way that each color is used precisely n2 times. Show that there is a line, parallel to an edge of the grid, which passes through at least points with distinct colors.
(5 pont)
A. 556. Prove that for arbitrary real numbers there exist a real t such that
(5 pont)
Upload your solutions above.
