A KöMaL 2012. márciusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2012. április 10-én LEJÁRT. |
I. 289. Gyermekkorunk egyik kedvelt játéka a dominó. Minden dominólap két nem negatív egész számból, illetve a két számnak megfelelő számú pöttyből áll. Egy \(\displaystyle N\) nagyságú (\(\displaystyle 0\le N\le 10\)) készletben minden szám 0 és \(\displaystyle N\) közötti. Két dominólap megegyezik, ha rajtuk a számok az olvasási sorrendtől függetlenül azonosak. Egy dominókészlet nem tartalmaz azonos dominókat.
Pédául egy 2-es dominókészlet a következő dominókat tartalmazza: [0 0] [0 1] [0 2] [1 1] [1 2] [2 2].
Első feladatunk, hogy állítsunk elő funkcionális algoritmussal az \(\displaystyle N\)-es dominókészletet. Az előállítást végző függvény bemenete \(\displaystyle N\) értéke, eredménye a dominólapok alábbi minta szerint rendezett sorozata.
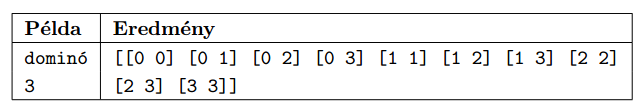
Második feladatunk, hogy készítsünk függvényt, amely egy \(\displaystyle N\)-es dominókészlet összes pöttyeinek számát adja meg.

Egy nagy családban több gyereknek is van dominója, melyek játék közben összekeveredtek egymással.
Harmadik feladatként adjuk meg, hogy a dominók között melyek azok, amelyek többször fordulnak elő. A függvény bemenete a dominólapok nem rendezett listája, kimenete egy a fentiekhez hasonló rendezett lista.
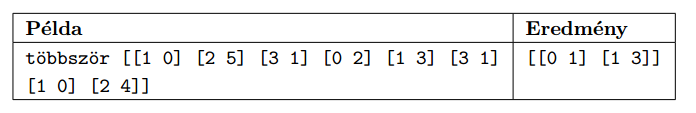
A megoldáshoz az Imagine Logo programozási környezetet ajánljuk, de a feladat megoldható Neumann-elvű programozási nyelvvel is (C, C++, Pascal, ...). A megoldás során - a be és kimenetektől eltekintve - csak a programozási nyelv funkcionális részét használjuk. Ne alkalmazzunk változókat, csak rekurzió segítségével valósítsunk meg az ismétlést. Igyekezzünk a megoldást minél több paraméterezhető függvényre bontani. A funkcionális programozásról az I. 259. feladatnál részletesen olvashatunk.
Beküldendő egy i289.zip tömörített állományban a megoldás forráskódja (i289.imp Imagine Logo Project, i289.pas, i289.cpp, ...) és egy i289.txt szöveges állomány, amely ismerteti a megoldás során készített függvényeket és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 290. A feladat megoldásához felhasználható állomány: deviza.txt
A bankoknál a hitelezés és a betétek kezelése mellett a fontos feladatok közé tartozik a különböző valuták átváltása, nyilvántartása is. Az egyes országok fizetőeszközei között folyamatosan változó értékviszony a gazdaság, a kereskedelem fontos adata. Ebben a feladatban a tavalyi év utolsó két hónapjának az OTP-nél nyilvántartott devizaárfolyamait elemezzük, használjuk. A devizaárfolyamot munkanapokon aktualizálják, ebből a szempontból az év utolsó két hónapja eléggé hektikus a hosszú hétvégék és az ünnepek miatt. A köztes munkaszüneti napokon az árfolyam a munkaszünet előtti utolsó munkanapéval azonos. Mivel november első napja is munkaszüneti nap, ezért erre a napra beiktattuk a táblázatba az aznapi aktuális (október 28-ai) árfolyamot.
A honlapunkról letölthetők az adatok a deviza.txt fájlban, ami egy tabulátorokkal tagolt, UTF-8 kódolású szövegállomány.
A megoldás során vegyük figyelembe a következőket:
-- A megoldás során törekedjünk képlet, függvény és hivatkozás használatára.
-- A megoldás során a V oszloptól jobbra, illetve az 56. sor alatt végezhetünk segédszámításokat.
[1.] Nyissuk meg táblázatkezelő program segítségével a deviza.txt fájlt úgy, hogy az első beolvasott adat az A1-es cellába kerüljön. A táblázatot mentsük a táblázatkezelő saját formátumában i290 néven. (A táblázat első két oszlopa a dátumot, első sora a devizák kódját, a második ezek megnevezését, végül a többi sorban az adott devizák aktuális középárfolyamát tartalmazza. Például a K28-as cellában található 348,58 érték azt jelenti, hogy 2011. december 5-én egy angol font értéke 348,58 Ft volt.)
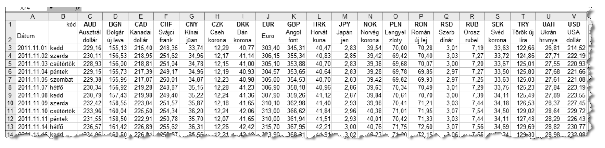
[2.] A C47:V47 tartományban adjuk meg, hogy mekkora volt az egyes devizák tágassága az adott időszakban, vagyis azt, hogy az egyes devizák legnagyobb értéke hányszorosa a legkisebb értéknek.
[3.] A C48:V48 tartományban minden devizanemnél jelenítsük meg, hogy az adott időszakban hány napon volt nagyobb az árfolyam az átlagosnál. A válasznál -- mind a napok számánál, mind az átlagszámításnál -- vegyük figyelembe a munkaszüneti napokat.
[4.] Egy befektető egy brókercégnél november 3-án beváltatott középárfolyamon a háromféle dollárra (ausztrál, kanadai és USA) 1--1 millió forintot. December 19-én visszaváltatta, amire 0,5% kezelési költséget számítottak fel neki. (A valóságban a pénzváltásnál vételi és eladási árfolyammal dolgoznak, a kettő különbözete a bank nyeresége. De ettől a számítás egyszerűsítése érdekében most eltekintünk, és a középárfolyamot használjuk, némi kezelési költséggel). A G54-es cellában adjuk meg, hogy mennyi volt ezen a tranzakción a befektető nyeresége. A cellához rendeljünk Forint pénznem formátumot tizedesek nélkül.
[5.] Az G55-ös cellában adjuk meg, hogy az adott időszakot tekintve hány devizának volt az időszak utolsó munkanapján (2011. december 30.) a legmagasabb az árfolyama.
[6.] A C52-es cellába írjunk olyan kifejezést, amely a C51-es és C50-es cellába írt adatokhoz meghatározza az aznapi árfolyamot, illetve az ,,Érvénytelen adat'' szöveget jeleníti meg, ha ahhoz nincs adatunk, akár 2011 utolsó két hónapjára érvényestől különböző dátum vagy akár más pénznem miatt. (Vigyázat! 2011. december 12-ére ismerjük az érvényes adatot, még akkor is, ha az alaptábla közvetlenül nem tartalmazza.) Például: ha C50: 2011.11.17.; C51: ,,NOK'', akkor a C52 cellában a 39,39 értéket jelenítsük meg.

Ha a két felette lévő cella közül bármelyik üres, a C52-es cella is legyen üres.
[7.] Készítsünk diagramot az amerikai dollár, a svájci frank és az euró árfolyam-ingadozásairól a teljes időszakra az alábbiak alapján:
a) a diagram csak a munkanapok adatait mutassa;
b) a diagram fajtája grafikon (vonaldiagram) legyen;
c) a diagramot új munkalapra hozzuk létre;
d) az USD vonala legyen vastag piros, az EUR-é vastag kék, a CHF-é pedig vastag fehér vonal. (A diagram és a jelmagyarázat területét állítsuk kellően sötétre, hogy a fehér vonal is jól látható legyen.)
e) a jelmagyarázat a diagram alá kerüljön;
f) a diagram címe ,,A vezető valuták árfolyamingadozása'' legyen;
g) a dátumban ne jelenjen meg az évszám, viszont az y tengely 200--340 tartományt fogja át, és jelenjen meg felette tengelyfeliratként az ,,Ft'' felirat.
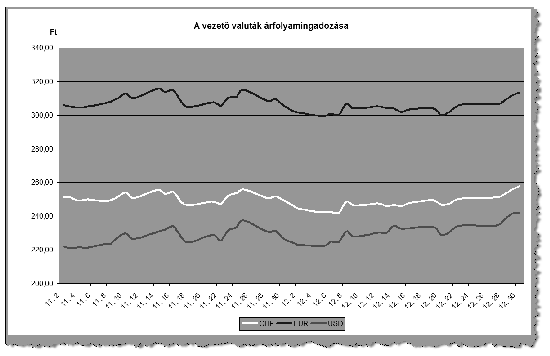
Az eredeti munkalapon a devizák kódját vastagítsuk meg, majd ezeket és a devizaneveket igazítsuk középre, mindkét irányban. A minta szerint legyen több soros a megnevezés, ha szükséges. Az A1:B2 tartomány is legyen a minta szerinti.
[8.] A kiszámított értékeket tartalmazó cellák háttérszíne legyen halványzöld, kerete sötétzöld.
Beküldendő a táblázatkezelő munkafüzet (i290.xls, i290.ods, ...), illetve egy rövid dokumentáció (i290.txt, i290.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
(10 pont)
I. 291. Létezik egy meglepően egyszerű, de igazán érdekes matematikai fejlesztő játék.
[] A játék néhány négyzet alakú, átlátszó plexi lapot tartalmaz, amelyekre különböző geometriai formákat festettek. A lapok egyszínűek, a festés helyén a lap nem átlátszó.
[] A játék során ezeket a lapokat kell egymás fölé pakolni egy -- a lapokkal egyező méretű -- keretbe. A festett részek a pakolás sorrendjében (részben) eltakarják egymást, így összességében érdekes formák alakíthatók ki. (Egy -- nem szimmetrikus festésű -- lap összesen nyolcféleképpen helyezhető el.)
[] A játékhoz tartozó rejtvényfüzet tartalmazza a kirakható alakzatokat.
Tervezzünk egyedi lapokat a fenti játékhoz. A lapok alakzatait 2-3 különböző szín alkalmazásával készítsük el.
Alkossuk meg a játék leírását tartalmazó dokumentumot, amely a játék ismertetésén, a lapok bemutatásán túl tartalmaz 10 feladványt is. (Egy feladvány legfeljebb 4 lap felhasználásával megoldható.) A feladványok megoldása az utolsó oldalon szerepel.
Ennek kiegészítéseként készítsünk a játék lényegét -- és egy feladvány megoldását bemutató -- néhány diából álló prezentációt.
Beküldendő a leírást (i291.pdf) és a bemutatót (i291.ppt, i291.odp, ...) tartalmazó i291.zip fájl.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2012. április 10-én LEJÁRT. |
S. 70. Béla szereti mindig jól átlátni a környezetét, így miután Nevesincs városba költözött, első dolga az volt, hogy rajzolt egy térképet a városról, és följegyezte rajta minden egyes utca hosszát -- természetesen mikrométerben, mivel a pontatlanságot ki nem állhatja. Ezek után persze az útvonalait is nagyon gondosan tervezi meg: most például azt eszelte ki, hogy úgy jusson el A-ból B-be, hogy az útvonalán előforduló leghosszabb és legrövidebb utca hosszának különbsége minimális legyen. Írjunk programot, amely meghatároz Béla számára egy ilyen tulajdonságú útvonalat.
A program a város leírását a standard bemenetről olvassa. Ennek első sorában egyetlen szóközzel elválasztva a kereszteződések N száma, illetve az ezeket összekötő utcák M száma található (1 N
N 1000, 0
1000, 0 M
M 5000). A második sor az A és B kereszteződések sorszámát tartalmazza, az ezt követő M darab sor pedig rendre egy-egy utcát ír le XiYiLi formátumban, ahol Xi és Yi az i-edik utca által összekötött két kereszteződés sorszáma, Li pedig az i-edik utca hossza (1
5000). A második sor az A és B kereszteződések sorszámát tartalmazza, az ezt követő M darab sor pedig rendre egy-egy utcát ír le XiYiLi formátumban, ahol Xi és Yi az i-edik utca által összekötött két kereszteződés sorszáma, Li pedig az i-edik utca hossza (1 Li
Li 109). Feltehetjük, hogy egy utca két végpontja mindig különbözik egymástól, valamint hogy nincs két olyan utca, melyek mindkét végpontja megegyezik. A kereszteződéseket 0-tól N-1-ig sorszámozzuk.
109). Feltehetjük, hogy egy utca két végpontja mindig különbözik egymástól, valamint hogy nincs két olyan utca, melyek mindkét végpontja megegyezik. A kereszteződéseket 0-tól N-1-ig sorszámozzuk.
A standard kimenet egyetlen sorába egy darab szám kerüljön: ha elérhető A-ból B, akkor az elérhető legkisebb különbség, ellenkező esetben pedig -1.

A maximális pontszám eléréséhez a programnak a legnagyobb teszteseteket is legfeljebb 1 másodperc alatt meg kell oldania.
Beküldendő egy tömörített s70.zip állományban a program forráskódja (s70.pas, s70.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s70.txt, s70.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrás melyik fejlesztőkörnyezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

