Problems in Physics, April 2012

M. 323. A beam of water, which hits a vertical plane surface perpendicularly, spreads out such that it has a parabolic boundary. (E.g. water coming from the shower hitting the side of the bathtub.) Measure how the focal length of this parabola depends on the speed of the water.

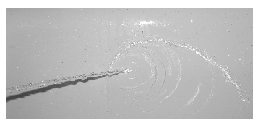
(6 points)

P. 4434. A pointlike lightsource ascends at a speed of v=0.8 m/s in a deep lake. There are no waves on the surface of the water. At what rate does the diameter of the circle created by the diffracted light on the surface of the water change? (The refractive index of water is n=4/3.)

(3 points)

P. 4435. There are 2 moles of Oxygen gas at a pressure of 0.2 MPa in a 15-liter container. What is the average speed of the molecules of the gas?

(3 points)

P. 4436. A tour boat departed at Siófok travelled at a constant speed of 18 km/h, first moved towards the North for a quarter of an hour, then it turned and travelled another quarter of an hour towards the West, then again turned and travelled a quarter of an hour towards the South, and then finally it travelled towards the East for a quarter of an hour.

a) Consider the curvature of the Earth and estimate how far will the tour boat be from the starting point at the end of the tour.

b) The mass of the boat is 500 tons. By what amount was the weight of the boat smaller when the boat travelled towards the East than when it travelled towards the West?

(4 points)

P. 4437. The two endpoints of an 8-m long weightless thread are fixed at the same height at a distance of 4 m. An object of mass 10 kg is hung onto the thread and can move frictionless.

a) What is the magnitude of the horizontal force that must be exerted on the object to keep it at rest on the thread exactly below one of the endpoints of the thread?

b) If the object is released from this position to what speed can it speed up?

(4 points)

P. 4438. A uniform solid disc of mass m=5 kg, and of radius R=10 cm is rotated at an angular speed of 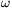₀=120 1/s about its symmetry axis, which is horizontal, and then it is carefully placed to the horizontal ground, such that it has no initial speed. The coefficient of friction between the disc and the ground is 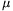=0.4.

Determine the work done by the frictional force on the disc, while the disc covers a distance of s=5 m. Show that the result is the same if the work-kinetic energy theorem is used or if the product of the force and the displacement is calculated.

(5 points)

P. 4439. A sample of Oxygen gas of mass 32 g is compressed at a constant pressure from a volume of 8 litres to a volume of 7 litres. During the process the gas is cooled down such that the pressure of the gas remains constant. At the final state the temperature is 40 ^oC smaller than at the initial state.

a) What was the initial and final temperature of the gas?

b) What is the pressure of the gas?

c) How much work was done in joules?

d) What is the amount of heat released by the Oxygen?

(4 points)

P. 4440. A hemispherical insulating shell is charged positively, and is fixed. The charge distribution on the shell is uniform. At a point on the symmetry axis, which is exactly at a distance of the radius measured from the centre of the hemisphere O, a small negatively charged bead is released. The speed of the bead is v₀ when it reaches the centre O.

What will the speed of the bead be when it reaches the shell? (Neglect the effect of gravity.)

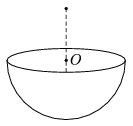
(5 points)

P. 4441. How much charge flows through the wire AB shown in the figure if the switch is closed and long enough time has elapsed.

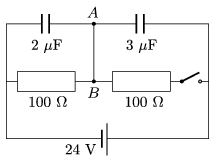
(4 points)

P. 4442. Radium decays into Radon by emitting an alpha particle: . The rest mass of the emitted alpha particle is 6.6^.10^-27 kg and its kinetic energy is 4.8 MeV. The half-life of radium is 1600 years.

a) What is the speed of the emitted alpha particle?

b) What is the activity of 1 kg ²²⁶Ra?

c) Determine the power of the radioactive source.

(4 points)

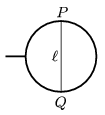
P. 4443. A soap film of surface tension 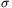is created in the frame, shown in the figure. The diameter of the frame is 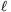. A piece of unstretched hair of length 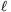, and of young modulus E joins the points P and Q. By what amount will the hair be elongated if the film in the right hand side is pricked by a hot pin. (The two endpoints of the hair are fixed and its weight is negligible. 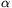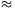For small angles use the approximation: sin 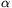-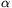³/6.)

(6 points)