KöMaL Problems in Informatics, May 2012
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on June 11, 2012. |
I. 295. Polybius (born in 200 BC) was a Greek historian and politician living in Rome. (We know about 40 volumes of his history books.) He invented the Polybius square to encode texts: each letter of the original text is mapped to a pair of letters (see the table, by using row and column coordinates). He used a 5×5 square to encode the 24 Greek letters, however, when we use the scheme with the English alphabet containing 2 more letters, both V and W are mapped to the pair UE.

During the encryption process, letters of the original text are replaced by the above vowel pairs first, then we choose some words at random from a list that contain these pairs.
The file szodb.txt contains all words of a long Hungarian text in alphabetical order. (Diacritical vowels have been replaced by the corresponding vowels without diacritical marks, further, each letter is capitalized.) From this list you can choose words that will contain the encrypted vowel pairs as embedded letters but in their original order.
Your program i295 should encode a given text. The command line argument to your program is the name of the file containing the word list. The original text to be encrypted (having maximal length of 100 characters) should be read from the keyboard. Then the words containing the vowel pairs should be displayed on the screen, separated by a space. In the example (Példa) the encrypted result is Eredmény.
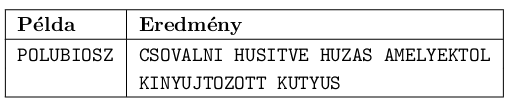
The source code (i295.pas, i295.cpp, ...) together with a short documentation (i295.txt, i295.pdf, ...) - also describing which developer environment to use for compiling, further a brief description of your solution - should be submitted in a compressed file i295.zip.
(10 pont)
solution (in Hungarian), statistics
I. 296. Environmental protection is emphasized more and more in our daily lives. Nowadays weather forecasts usually include some data on air pollution as well. Budapest has 11 different locations to monitor air quality and various pollutant concentrations. In this exercise you are going to work with the data collected during the first two months of 2012 by the Hungarian Air Quality Network, http://www.kvvm.hu/olm.
[1.] Create an empty database with name i296. Import data into this database from the text files allomasok, detektorok, hatarok and meresek, downloadable from our web page. (Table names in the database should be the same as the corresponding file names. The first lines of these UTF-8 encoded, tabulator separated files contain the field identifiers.) The relation between the tables is described by the figure. The ertek field of the file meresek is empty if the given detector on the given day did not yield any measurement.
Tables:


[2.] Create a query to determine which pollutants were not measured by the stations on January 18, 2012. The query should show the fields telepitesihely and sznev. (2jan18hiba)
[3.] Make a query to list for each station the pollutants without any collected data during the 60 days. The query should show the fields telepitesihely and sznev. (3vegiguzemenkivul)
[4.] Make a parametric query to list data for stations with detectors measuring the pollutants corresponding to szjeloles. (4holmerheto)
[5.] Determine by a query the average value and the quality range of ``nagyszemcsés szálló por koncentráció'' (concentration of large-particle floating dust) in January. (5janporminoseg)
[6.] List the station names and dates for each pollutant with maximal concentration during the first 2 months of the year. The list should be sorted according to date. (6maximumok)
[7.] Describe the effect of the increased traffic during working days on air pollution. Create a query to determine the average values of nitrogen oxides (NO, NO2, NOx) and sulphur dioxide (SO2) during working days and over the weekend, moreover, calculate the percentage of the weekend average versus the workday average. (7kozlekedesihatas)
[8.] For each station, determine the ratio between the maximal and minimal concentration of each pollutant. The 10 pollutants with highest ratio should be displayed together with fields telepitesihely, sznev and the actual ratio. (8nagyvaltozas)
Your database (i296.mdb, i296.accdb, i296.odb, ...) together with a short documentation (i296.txt, i296.pdf, ...) - also describing the name and version number of the database application - should be submitted in a compressed file i296.zip.
Downloadable files: allomasok.txt, detektorok.txt, hatarok.txt, meresek.txt.
(10 pont)
solution (in Hungarian), statistics
I. 297. In this task you are going to expand the table in Problem I. 281. of the 2011 December issue of our Journal, in such a way that by pressing a button it should be able to create diagrams with the content and format presented there for each class, further, it should fill the column of every student with a color corresponding to their talent levels.
You should use your previous solution or one of the files of the uploaded sample solutions. Delete the diagram created for the first class and make a command button to the right of the talent level part of the table. The macro or program associated with this command button should create the diagrams one below another corresponding to the classes and similar to the original ones in Problem I. 281.
Talent levels should be encoded by colors red, pale orange, yellow, light green, dark green, grey, light blue and dark blue, respectively, ranging from the 0th level to Level 7.
The spreadsheet (i297.xlsm, i297.xls, i297.ods, ...) containing your solution together with a brief description (i297.txt, i297.pdf, ...) should be submitted in a compressed file i297.zip.
(10 pont)
 |
Problems with sign 'S'Deadline expired on June 11, 2012. |
S. 72. Pieces of baggage of airport passengers who just landed are reloaded several times and put onto conveyor belts. However, different pieces of baggage of a given passenger may not be put adjacent to one another on the belt, which is undesirable: passengers would like to see their baggage arriving in one group. Your task is to put the different pieces of baggage of each passenger adjacent to one another on the belt such that the total distance of moving those pieces is minimal.
The conveyor belt is divided into segments of equal length. A segment is either empty or carries exactly one piece of baggage. (The length of a segment was determined in such a way that it can carry any type of luggage.) An airplane carries at most 40 people, and each person can carry at most 40 pieces of luggage. The conveyor belt for a given airplane has 1000 segments. The movement distance of a piece is defined as the difference between the position of the final segment and the initial segment of that piece. In the example, the piece denoted by ``t'' in the 9th position is moved into the 5th position, hence we had a movement distance equal to 4.
Your program should read the standard input: the first line of the input contains the length of the belt, while the second line contains the description of the pieces of baggage on the segments. Your program should rearrange the content of the belt with the minimal movement distance according to the requirement above. Your program should write the required total number of movements in the first line of the standard input, while the second line should contain the rearranged belt. Empty segments on the belt are denoted by dashes (-), while pieces of luggage of a given passenger are denoted by lowercase letters of the English alphabet. The input and output describe the part of the belt carrying pieces.
In the example, ``Példa bemenet'' is the sample input, while ``Példa kimenet'' is the corresponding output.
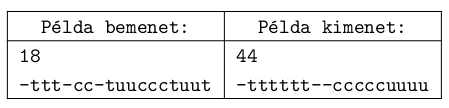
The source code (s72.pas, s72.cpp, ...) without the .exe or any other auxiliary files generated by the compiler should be submitted in a compressed file s72.zip, also containing a short documentation (s72.txt, s72.pdf, ...) with a brief description of your solution and the name of the developer environment to use for compiling.
(10 pont)
$Var(Body)
Upload your solutions above
