A KöMaL 2012. szeptemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2012. október 10-én LEJÁRT. |
I. 298. Adott egy N×N-es négyzet alakú biliárdasztal, amelynek szélén a golyók tökéletesen rugalmasan ütközhetnek. A golyók kiterjedés nélküliek és kezdetben az asztal egész koordinátájú pontjaiban állhatnak.
Készítsünk programot i298 néven, amely megadja és a standard kimenetre kiírja, hogy egy adott (k;l) koordinátájú pontból gurítva egy golyót, azzal egy másik adott (x;y) koordinátájú golyót hányféle úton találhatunk el.
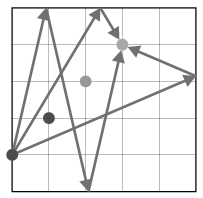
Példa három lehetséges útra
A golyó útja akkor érvényes, ha legföljebb két falon pattan vissza anélkül, hogy a megcélzott golyón kívül más golyót érintett volna. Ha egy golyó pont az asztal sarkát találja el, akkor önmagába verődik vissza, mivel ez mindkét falról történő visszapattanásnak számít. A program eredménye -- az asztal szélén történő visszapattanások száma szerint -- a kétpattanásos, az egypattanásos és a pattanás nélküli utak száma.
A program parancssori argumentuma legyen a kezdőfeltételeket leíró adatállomány neve. A fájl első sorában N (2 N
N 50) az asztal méretét, M (1<M
50) az asztal méretét, M (1<M 20) a golyók számát adja meg. Az ezt követő M sor a golyók koordinátáit, majd az utolsó sor a golyóindítás (k;l) koordinátáit (1
20) a golyók számát adja meg. Az ezt követő M sor a golyók koordinátáit, majd az utolsó sor a golyóindítás (k;l) koordinátáit (1 k,l
k,l N), és a célgolyó (x;y) koordinátáit írja le. A biliárdasztal bal alsó sarka legyen az (1;1) koordinátájú pont, és az első koordináta jobbra, a második koordináta felfelé nő.
N), és a célgolyó (x;y) koordinátáit írja le. A biliárdasztal bal alsó sarka legyen az (1;1) koordinátájú pont, és az első koordináta jobbra, a második koordináta felfelé nő.
Példa (lásd az ábrát):

Beküldendő a program forráskódja (i298.pas, i298.cpp, ...) és rövid dokumentációja (i298.txt, i298.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 299. Egy fűszerforgalmazó cég új termékcsaláddal jelentkezik a piacon. Az új termékcsoport neve: Minden ízében íz. A termékek a nevükhöz illően fűszerkeverékek. A fűszerkeverékek nevét, összeállítási receptjét és az alapfűszerek adatait egy adatbázisban tárolják.
Az adatbázis három táblából áll:

A táblák kapcsolatát az ábra mutatja:

Hozzunk létre i299 néven egy adatbázist.
Importáljuk az UTF-8 kódolású, a táblák nevével megegyező nevű, honlapunkról letölthető szövegfájlokból az adatokat. Ügyeljünk a kapcsolatok megadására.
Készítsük el az alábbi kérdésekre válaszoló lekérdezéseket.
[1.] Adjuk meg azon fűszerkeverékek nevét, amelyek tartalmaznak kurkumát. (01kurkuma)
[2.] Adjuk meg a Szecsuáni fűszerkeverék összetevőit és azok mennyiségét, részarány szerint csökkenő sorrendben. (02szecsuani)
[3.] Adjuk meg, hogy melyik keverék tartalmazza a legtöbbféle összetevőt, és hogy szám szerint mennyit. (03legtobbfele)
[4.] A cég mindegyik fűszerkeverékből 100-100 darab 100g-os mintát készít, hogy ingyenes termékmintaként szétküldhesse. Mennyibe kerülnek összesen az ehhez felhasznált fűszerek? (04mintaar)
[5.] Egy hajóbaleset miatt időlegesen nem lehet beszerezni a szecsuáni borsot és a kardamomot. Listázzuk ki, hogy melyik fűszerkeverékek készítésével kell leállni. Minden keverék neve legfeljebb egyszer jelenjen meg. (05nemkeverheto)
[6.] Az előző feladat feltételei szerint adjunk választ arra, hogy melyik keverékek előállítását nem kell szüneteltetni. (06keverheto)
[7.] Adjuk meg a sót nem tartalmazó fűszerkeverékek nevét, legnagyobb részarányú összetevőjének nevét és annak kilónkénti tömegét. (07sotlan)
[8.] Adjuk meg a Mediterrán és a Flekken keverékek közös összetevőinek listáját. Csak a fűszer fajtája számít a mennyiségétől függetlenül. (08mfkozos)
[9.] Adjuk meg, hogy mely összetevőkben tér el a Grill és a Pikáns Grill keverék (azon összetevők nevét, amelyek csak az egyik keverékben szerepelnek). Itt is csak a fajta számít. (09grilldifi)
[10.] Soroljuk fel azon fűszerkeverékeket, amelyekben a legdrágább fűszert felhasználják. Jelenjen meg e fűszer 1 kg keverékre vetített ára is keverékenként. (10draga)
Beküldendő az adatbázis (i299.mdb, i299.accdb, ...), illetve egy rövid dokumentáció (i299.txt, i299.pdf, ...), amelyben szerepel a megoldáskor alkalmazott adatbázis-kezelő neve, verziószáma.
Letölthető fájlok:
(10 pont)
I. 300. 175 éve, 1837. szeptember 4-én mutatta be New Yorkban Samuel Morse az általa alkotott telegráfot, s ezzel forradalmasította a távközlést.
Készítsünk a Morse-távíró bemutatására weblapot. A weblapba építsünk be egy interaktív részt is a következő formában:
legyen rajta egy beviteli mező, amelybe az angol ábécé karaktereit tartalmazó szöveget írhatunk (elegendő, ha 40 karakternyi szöveget fel tudunk dolgozni);
a beviteli mezőben szereplő szövegnek megfelelő pont-vonal kombinációt egy ,,szalagon'' animációval jelenítsük meg vagy megfelelő hosszúságú sípolásokkal tegyük hallhatóvá.
Beküldendő a weblapot tartalmazó mappa tömörítve (i300.zip), amely tartalmazza a HTML dokumentumokat (a kezdőlap index.html nevű legyen), képeket, hangokat és más, offline megjelenítéshez szükséges állományokat is. A szöveges és képi források feltüntetéséről se feledkezzünk meg.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2012. október 10-én LEJÁRT. |
S. 73. Nevenincs városban pingpongversenyt készülnek rendezni. Minden versenyzőről tudjuk a lakhelyét, és azt, hogy mennyit hajlandó gyalogolni egy mérkőzés kedvéért. A város alakja erősen elnyújtott, úgyhogy a pontos lakcím helyett csak azt vesszük figyelembe, hogy a város hosszú főutcájának melyik részéhez lakik közel a versenyző, amit egy házszámmal adunk meg, valamint a gyaloglási távolságot is csak a főutca mentén mérjük. (Azaz úgy tekintjük, hogy bárki el tudja érni a főutcát elhanyagolható idő alatt.)
Két adott lakó között pontosan akkor jöhet létre mérkőzés, ha legalább az egyikük hajlandó elsétálni a másikhoz (a mérkőzést mindenképpen valamelyik játékos lakhelyén kell megrendezni), vagyis a házszámuk közötti különbség legfeljebb akkora, amennyit a lelkesebb fél hajlandó gyalogolni.
Írjunk programot, amely meghatározza, hogy a versenyen hányféle mérkőzés jöhet létre. Két mérkőzést akkor tekintünk különbözőnek, ha nem ugyanaz a két játékos vesz részt benne.
A program a standard input első sorából beolvassa a versenyzők számát (). A következő N sorban egy-egy versenyzőről található a két ismert adat, két darab, szóközzel elválasztott szám formájában: az első a lakcíme (
), míg a második megadja, hogy mennyit hajlandó gyalogolni egy mérkőzés kedvéért (
).
A standard outputra írjunk ki egyetlen számot: a lejátszható mérkőzések számát.
Példák:

Pontozás: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 2 pontot ér. A programra akkor kapható meg a maximális 8 pont, ha bármilyen, a feltételeknek megfelelő tesztesetet képes megoldani a 3 mp futási időlimiten belül. Kapható részpontszám, ha a program csak kisebb tesztesetekre tud lefutni időben, továbbá akkor is, ha a program csak olyan teszteseteket tud megoldani, amiknél a versenyzők által megadott gyaloglási távolságok mind azonosak.
Beküldendő egy tömörített s73.zip állományban a program forráskódja (s73.pas, s73.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s73.txt, s73.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

