A KöMaL 2013. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2013. március 11-én LEJÁRT. |
I. 313. A fák évgyűrűi az évszakok miatt alakulnak ki a mérsékelt éghajlati övben. A fák télen és nyáron eltérő mértékben növekednek. Az évgyűrűk vastagsága között különbség van, mert a növekedés mértékére hatással van például az adott időszakban az időjárás szárazabb vagy csapadékos jellege. Az évgyűrűk vizsgálata így lehetővé teszi az éghajlat kutatását. A dendrokronológiát a régészek szívesen használják kormeghatározásra. Ha azonos éghajlatú területen két fa eltérő időpontban ,,született'', de életükben volt közös szakasz, akkor abban az időszakban az évgyűrű szerkezete hasonló. Ennek segítségével több fa évgyűrűmintázata összeilleszthető. Egyes területeken a régészek évezredekre visszamenő pontos kronológiával rendelkeznek.
Adott N fa évgyűrűmintája, azaz az évgyűrűk vastagsága milliméter pontossággal. A mintavétel módszerének részleteitől, statisztikai feldolgozásának elemzésétől most eltekintünk.
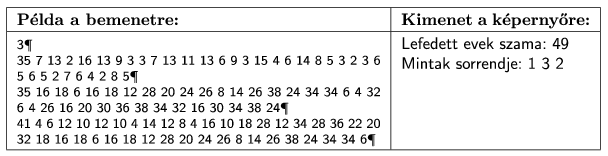
A fák eltérő fajúak és korúak lehetnek, ezért a minták illesztésénél az egymás utáni évgyűrűvastagságok arányainak sorozatát hasonlítjuk össze. Például az egyik mintában a 6, 4, 2, 8, 5 milliméter széles gyűrűk esetén az összehasonlítást 0,66, 0,50, 4,00, 0,62 sorozattal végezzük.
Az illesztést akkor tekintjük jónak, ha legalább 10 arány legföljebb egy százalék hibával azonos és a hátralévő részében rövidebb minta minden aránya megegyezik a hosszabbikéval. Vegyük figyelembe, hogy akár több minta is illeszkedhet. A legrégebben kifejlődött fa évgyűrűmintája szerepel elsőként a fájlban tárolt mintázatok között.
Készítsünk programot i313 néven, amely megadja N évgyűrűminta esetén a legtöbb évet lefedő, az elsőből induló, illeszkedő mintasorozatát és ehhez a minták sorrendjét. A képernyőn az évek számát és a minták sorrendjét jelenítsük meg.
A program parancssori argumentuma legyen az évgyűrűminták adatait leíró adatállomány neve. A fájl első sorában N (2 N
N 50) a minták számát adja meg. Az ezt követő N sor az egyes minták adatait adják meg. Minden sor első értéke H (10
50) a minták számát adja meg. Az ezt követő N sor az egyes minták adatait adják meg. Minden sor első értéke H (10 H
H 500) az adott minta évgyűrűinek száma, majd H darab egész szám, az évgyűrűk szélességei következnek.
500) az adott minta évgyűrűinek száma, majd H darab egész szám, az évgyűrűk szélességei következnek.
Beküldendő a program forráskódja (i313.pas, i313.cpp, ...) és rövid dokumentációja (i313.txt, i313.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 314. A környezetvédő tudósok vélekedése szerint a globális felmelegedés egyik fontos oka az üvegházhatású gázok fokozódó kibocsátása a légkörbe. A nemzetközi szervezetek ezért komolyan számon tartják az egyes országokban folyó gazdálkodás ilyen irányú hatását is. Üvegházhatású gázoknak nevezzük azokat a gázokat, amelyek a légkörbe kerülve csökkentik annak ,,átlátszóságát'' az infravörös sugárzásra. Az egyes gázok ilyen jellegű hatása eltérő, így azok hatását széndioxid egyenértékben mérik. Ez az egyenérték egy tonna CO2 hatásával egyenértékű.
Az ipar és a mezőgazdaság folytán a környezetbe kerülő legjelentősebb üvegházhatású gázok: a szén-dioxid (CO2), a metán (CH4), a dinitrogén-oxid (N2O), a fluorozott szénhidrogének (CHF3, CH2FCF3, C2H3F3), a perfluor-karbonok (CF4, C2F6, C3F8, C6F14), a kén-hexafluorid (SF6), a telített freonok (CFCl3, CF2Cl2, CF2CFCl3), a halonok (CBrClF2, CBrF3) és a telítetlen freonok (CHF2Cl, CH3CF2Cl).
Az EuroStat adatbázisa alapján a KSH közzéteszi az EU egyes országainak üvegházhatású gáz kibocsátási adatait. Ebből az adatbázisból készülnek átfogó elemzések, most mi is megpróbálunk néhány vizsgálathoz adatokat biztosítani. Az adatbázis adatai az 1990 és 2010 közötti időszakra vonatkoznak, és ezer tonna széndioxid-egyenérték egységben értendők.
Honlapunkról letölthetők az adatok az uveghaz.txt fájlból, ami egy tabulátorokkal tagolt, UTF-8 kódolású szövegállomány.
A megoldás során vegyük figyelembe a következőket:
- A megoldás során törekedjünk képlet, függvény és hivatkozás használatára.
- A megoldás során az AC oszloptól jobbra, illetve a 250. sor alatt végezhetünk segédszámításokat.
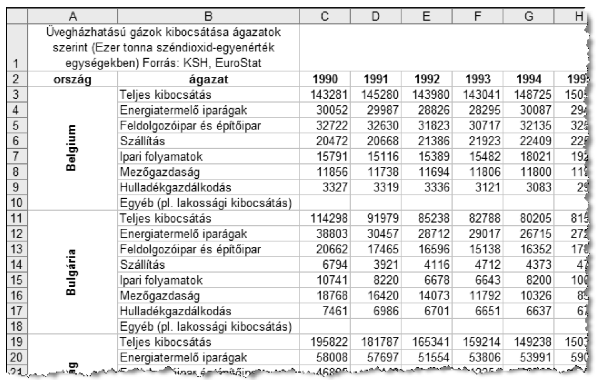
1. Nyissuk meg táblázatkezelő program segítségével az uveghaz.txt fájlt úgy, hogy az első beolvasott adat az A1-es cellába kerüljön. A táblát mentsük a táblázatkezelő saját formátumában i314 néven.
2. Számítsuk ki az egyes országokra évente - a hiányzó, de a Teljes kibocsátás sorából és az ágazati adatokból kiszámítható - az egyéb kibocsátás értékét (10., 18. stb. sorokban).
3. Az X, Y és Z oszlopokban számítsuk ki minden adatsorra a kibocsátás maximumát, minimumát és átlagát.
4. Az AA oszlopban adjuk meg minden adatsorra, hogy az melyik vizsgált évben érte el a maximumát.
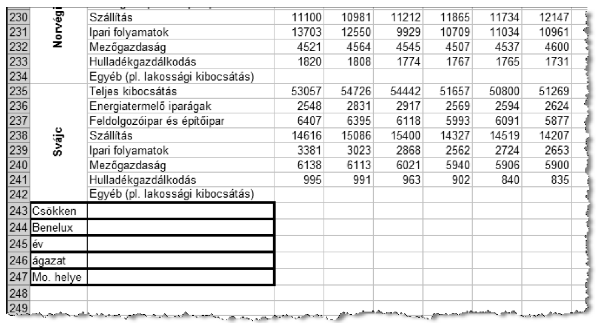
5. A B243-as cellában adjuk meg, hogy hány ország Hulladékgazdálkodás ágazati kibocsátása mutatott 2000-től 2010-ig csökkenő tendenciát, vagyis a kibocsátás évről évre csökkent.
6. A B244-es cellában adjuk meg, hogy a vizsgált időszakban hány évben haladta meg a Benelux államok (Belgium, Hollandia, Luxemburg) teljes kibocsátásának 9%-át a három ország mezőgazdaságából keletkező kibocsátás?
7. A B247-es cellába írjunk olyan kifejezést, amely a B245-ös és B246-os cellába írt adatokhoz meghatározza, hogy abban az évben, abban az ágazatban hány ország kibocsátása nagyobb a magyarországi ágazati adatnál. Ha a két felette lévő cella közül bármelyik üres, a B247-es cella is legyen üres.
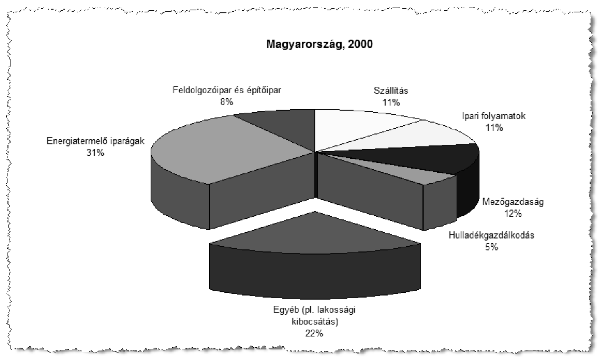
8. Ábrázoljuk egy új munkalapra készített tortadiagramon Magyarország 2000. évi ágazati adatait. A diagramról az ágazat neve és adatának százalékos értéke legyen leolvasható. Az egyébhez tartozó szelet - a minta szerint - forduljon szembe, és legyen a diagramból kiemelve. A diagram kapja a ,,Magyarország üvegházhatású gázainak kibocsátói'' címet.
9. Hajtsuk végre a mintán látható formázásokat (cellaegyesítés, igazítás, szegélyezés, vastagítás).
Beküldendő a táblázatkezelő munkafüzet (i314.xls, i314.ods, ...), illetve egy rövid dokumentáció (i314.txt, i314.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
Mintákat láthatunk a mellékelt ábrákon.
Letölthető fájl: uveghaz.txt
(10 pont)
I. 315. Azt kaptuk feladatul, hogy készítsük el a KöMaL pontversenyén részt vevő iskolák rangsorát. A lista évenként készüljön, a sorrend az induló diákok száma szerint legyen csökkenő. A 2010/2011-es tanév listája például a
http://www.komal.hu/eredmeny/eredmeny.h.shtml?a=isklist&ev=2010 címen érhető el. Az url utolsó négy karakterének értelemszerű módosításával a többi év adatai is hozzáférhetők 2001-től.
A rangsor az alábbi táblázatos formában készüljön:

A feldolgozást kézzel is elvégezhetnénk, azonban az meglehetősen időt rabló megoldás, ezért egy tapasztaltabb informatikustól kértünk tanácsot. Ő ránézett néhány ilyen oldalra, majd azt mondta, PHP nyelven írt programmal oldaná meg a feladatot. Mivel PHP-ben nem, de más nyelven tudunk programozni, ezért megkértük, hogy vázolja a megoldást. A vezérlési szerkezetek és néhány utasítás ismerősnek tűnt, ezért csak néhány szót, kifejezést jegyeztünk le, amely ,,jól jöhet'': strip_tags, explode, asszociatív tömb. A program fejlesztéséhez a XAMPP multiplatform eszközt ajánlotta és megemlítette, hogy a PHP-ről minden megtalálható az online dokumentációban a www.php.net címen.
Tehát a feladat adott: írjunk programot PHP nyelven, amely például a 2009/2010-es tanév rangsorát az i315.php?ev=2009 címen megjeleníti a böngészőben.
Beküldendő a program forráskódja (i315.php) és rövid dokumentációja (i315.txt, i315.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja a megoldás során használt PHP verziószámát.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2013. március 11-én LEJÁRT. |
S. 78. Bergengóciában a tudósok egy új növényfélét szeretnének vizsgálatoknak alávetni. Mivel a növénynek igen speciális igényei vannak, így a tudósok mindenképp egy összefüggő területen (tehát szomszédos parcellákon) szeretnék termeszteni. Ehhez rendelkezésükre áll N egymást követő parcella: . Bergengóciában nagyok a szintkülönbségek az egyes parcellák között. Ismert minden parcellának a tengerszint feletti magassága: ai pozitív egész (
). Ráadásul a növényt csak olyan parcellákon lehet termeszteni, ahol bármely két parcella szintkülönbsége nem halad meg egy T korlátot:
. A tudósok a növényt a rendelkezésre álló parcellák közül minél több parcellán szeretnének termeszteni. Adjuk meg a maximális elérhető parcellaszámot.
A program olvassa be a standard input első sorából N-et és T-t, majd a következő sorból az ai szóközzel elválasztott egészeket, és írja a standard output első és egyetlen sorába a maximális parcellaszámot.
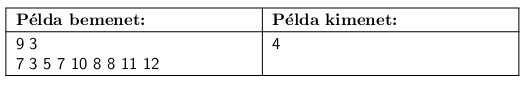
Magyarázat: a 7, 10, 8, 8 magasságú parcellák megfelelőek, de akár a 10, 8, 8, 11 is helyes 4 hosszú parcellasorozat; 5 hosszú nincsen.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a 2,5 mp futásidőkorláton belül. Mivel a bemeneti állomány nagy, ezért érdemes beleszámolni, hogy a legnagyobb tesztesetek beolvasása önmagában 2 mp időbe telhet. Kapható részpontszám a 9 pontból, ha a program csak kisebb tesztesetekre tud lefutni időben. Az alábbi korlátok érvényesek az egyes részmegoldásokra:
2 pontért:
;
további 3 pontért:
;
további 4 pontért:
.
Beküldendő egy tömörített s78.zip állományban a program forráskódja (s78.pas, s78.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s78.txt, s78.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

