A KöMaL 2013. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2013. május 10-én LEJÁRT. |
M. 332. Vékony, rugalmas acéllemezt (például egy kés pengéjét vagy egy fűrészlapot) fogjunk satuba úgy, hogy legfeljebb 10 cm-es része álljon ki a satuból. A kiálló rész vége lehet gömbölyű, vagy akár hegyes is, nem kell a lemeznek pontosan téglalap alakúnak lennie. Pendítsük meg ezt a kiálló részt! Mérjük meg, hogyan függ a megpendített lemez f rezgésszáma (a hallott hang magassága) a rezgésbe hozott rész középvonalának  hosszától!
hosszától!
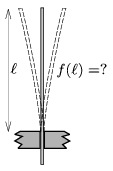
Közli: Radnai Gyula, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2013. május 10-én LEJÁRT. |
P. 4529. A kávé a csészében fekete, a habja viszont fehér vagy krémszínű. Miért?
Észtországi feladat
(3 pont)
P. 4530. Egy T=2 cm magas tárgyról egy gyűjtőlencse K=4 cm magasságú, fordított állású képet alkot. Szerkesztéssel határozzuk meg a lencse fókusztávolságát!
Szegedi Ervin (1956-2006) feladata
(3 pont)
P. 4531. Hogyan kell adott mennyiségű sörétet elosztani az ábrán látható kocsi és serpenyő között, hogy a fonalat feszítő erő a lehető legnagyobb legyen? (A csiga tömege elhanyagolható.)
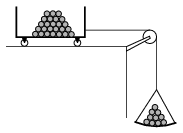
Párkányi László (1907-1982) feladata
(4 pont)
P. 4532. Az ábrán szereplő kapcsolásban az izzólámpák egyformák, U feszültség esetén a teljesítményük P. A kapcsolók nyitott (ny) és zárt (z) állásai esetén melyik és mekkora teljesítménnyel világít? Töltsük ki a táblázatot!
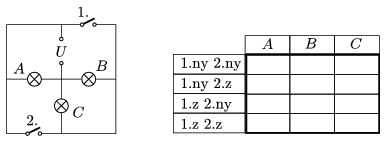
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4533. Egy diák állva utazva a buszon nem kapaszkodott meg, mialatt a busz éppen kanyarodott, ezért elesett. Mekkora szögben kellett volna megdőlnie, hogy ne essen el, ha a busz 25 m sugarú kanyarban 30 km/h sebességgel haladt?
Közli: Juhász Péter, Budapest, Piarista Gimnázium
(4 pont)
P. 4534. Mekkora az ábrán látható kapcsolásban az R változtatható ellenállás értéke, amikor
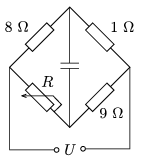
a) a kondenzátor töltetlen;
b) a kondenzátor feszültsége éppen fele U-nak?
Közli: Légrádi Imre, Sopron
(4 pont)
P. 4535. A mellékelt (az első borítón is látható) fényképen a fogyó Hold egy fázisát láthatjuk. A kép méreteit felhasználva határozzuk meg, hogy a felvétel készítése előtt hány nappal volt telihold!

Közli: Dégen Csaba, Budapest
(4 pont)
P. 4536. A szélerőművek hatásfokának elvi határa az ún. Betz-limit, amely 59,3% (lásd cikkünket lapunk 246. oldalán). További veszteségek is fellépnek, de a legkorszerűbb erőművek megközelítik a Betz-limit 84%-át.
a) Hány megajoule mozgási energia érkezik 1 másodperc alatt a 27 km/h sebességű légáramban arra a turbinára, amely 100 méter magas, lapátjainak hossza pedig 44 méter?
b) Mekkora a turbina maximális kimenő elektromos teljesítménye ekkora szélsebesség mellett?
Öveges József emlékverseny, Tata
(4 pont)
P. 4537. Egy élelmiszerboltban henger alakú trappista sajtot vásároltam. A pénztárhoz érve a sajtot az álló futószalagra helyeztem az ábrának megfelelően úgy, hogy a henger alkotója merőleges volt a futószalag széleire. Amikor a futószalag elindult, a sajt is mozgásba jött. Mekkora lett a sajt középpontjának sebessége, ha a futószalagé 60 cm/s volt?
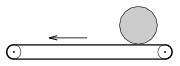
Közli: Vigh Máté, Budapest
(5 pont)
P. 4538. Az ábra szerinti, könnyen mozgó kiskocsira negyedkör keresztmetszetű, R=20 cm sugarú, súrlódásmentes lejtő van erősítve. A kocsi vízszintes felülete érdes, a súrlódás együtthatója 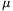 =0,8. A kocsi platója felett h=2R magasságból szabadon esik egy pontszerűnek tekinthető test, és érintőlegesen érkezik a lejtő tetejére. Végigcsúszva a pályáján éppen a kocsi szélén áll meg. Milyen hosszú a kocsi?
=0,8. A kocsi platója felett h=2R magasságból szabadon esik egy pontszerűnek tekinthető test, és érintőlegesen érkezik a lejtő tetejére. Végigcsúszva a pályáján éppen a kocsi szélén áll meg. Milyen hosszú a kocsi?
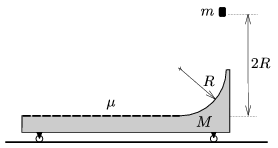
Közli: Holics László, Budapest
(5 pont)
P. 4539. Egy 4r magas, tömör, egyenes henger alapja r sugarú kör. Egy kemény, de rugalmas anyagú vízszintes asztal egyik fele csúszós, a másikon pedig 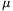 a súrlódási együttható. A két részt egy egyenes vonal választja el egymástól. A hengert alaplapjával az asztal csúszós oldalára helyezzük, majd meglökjük az elválasztó vonalra merőleges irányban. Felborul-e a henger a választóvonal elérése után (és ha igen, hogyan), amennyiben
a súrlódási együttható. A két részt egy egyenes vonal választja el egymástól. A hengert alaplapjával az asztal csúszós oldalára helyezzük, majd meglökjük az elválasztó vonalra merőleges irányban. Felborul-e a henger a választóvonal elérése után (és ha igen, hogyan), amennyiben
a) 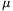 =0,2;
=0,2;
b) 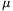 =0,7;
=0,7;
c) 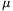 =1,4?
=1,4?
(Az m tömegű, r sugarú, 4r magas henger tehetetlenségi nyomatéka a vízszintes súlyponti tengelyre .)
Közli: Várkonyi Péter, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

