KöMaL Problems in Informatics, May 2013

Problems with sign 'I' Deadline expired on June 10, 2013.

---

I. 322. Many of us like playing various word games. Rules are typically illustrated by giving examples or solutions. For the following word games, we have used the novel Egri csillagok by Géza Gárdonyi as a source. The file szoveg.txt downloadable from our site contains selected words from this novel; all written in lowercase letters of the English alphabet, having length at most 20 characters, and each word is put in a separate line to make their processing easier.

Your program i322 should solve the following tasks by using the words of the szoveg.txt file given as a command line argument to your program. Your solution should be able to handle input text files of arbitrary length.

Whenever the output of your program is to appear on the screen, the number of the actual task should be displayed. If the program prompts the user for input, display what kind of data is expected (for the first task, for example, ``Task #1: Please enter a word:''). By default, the words in your screen output should be separated by a space character. Diacritical marks in the output can be omitted.

1. Ask the user to enter a word and decide whether it contains only one kind of vowel of the English alphabet (a, e, i, o, u). If yes, then display ``It contains only one kind of vowel''. If the entered word contains none or more than one kind, then display ``The statement is false''. We can suppose that the entered word contains only lowercase English letters.

2. Count and display the number of words of the file szoveg.txt in each of the following categories: words with only back vowels (a, o or u), words with only front vowels (e or i), and words with both back and front vowels. You should also display the size of these groups compared to the total number of words, expressed as percentages to 2 decimal digits.

For example:

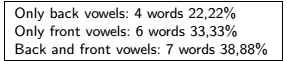
3. Ask the user to enter a string (that is, characters without spaces) of length of at most 20 characters, then collect and display on the screen all the words that contain this string.

4. Collect and display on the screen all the words that consist of letters in alphabetical order.

For example:

5. Collect the words such that by omitting their first and last letters we get a word also from the file szoveg.txt.

6. Find and display 10 words from the list that can be cut into two identical parts.

Two examples:

7. Create a file kettevag.txt containing 100 words from the list, each in a separate line, with the following property: if a word is suitably cut into two (not necessarily in the middle), then the resulting two parts are also words from the file szoveg.txt.

Two examples:

The source code (i322.pas, i322.cpp, ...) together with a short documentation of your program (i322.txt, i322.pdf, ...), also containing the name of the developer environment to use for compiling and a brief description of your solution, should be submitted in a compressed file (i322.zip).

Downloadable file: szoveg.txt

(10 pont)

solution (in Hungarian), statistics

---

I. 323. We would like to develop an information display system for passengers travelling with Tram No. 1 in Debrecen, Hungary. The (tabulator separated and UTF-8 encoded text) file menetrend.txt containing its timetable during the school year can be downloaded from our homepage.

Open the file menetrend.txt in the spreadsheet application so that the first piece of data of that file appears in cell A1. Then save the data table with name i323 using the default file format of your spreadsheet application.

The tram service operates in a circular route beginning and ending with Nagyállomás station. In column A of the worksheet menetrend (= timetable), absolute starting times (= indulási idő) from each station are listed. Column C contains station names (= megállóhelyek), while column D the travel times between consecutive stations (= szakaszidő) in minutes (= perc).

In column E, you should determine for each station the relative travel time from Nagyállomás (= menetidő), by using a similar format as in the example. Due to the circular route, several station names occur twice.

The next worksheet tájékoztató (= information) should contain the following messages, according to the example. (The translation of the messages in the example is as follows. Cell A1: ``Where would you like to start from?''; cell A2: ``What time would you like to start?''; cell A3: ``What is your destination?''; cell D1: ``The given data are:''; cell D2: ``Get on the vehicle at:''; cell D3: ``Arrival time at the destination:''; cell D4: ``Number of stations:''; cell D5: ``Travel time:''.)

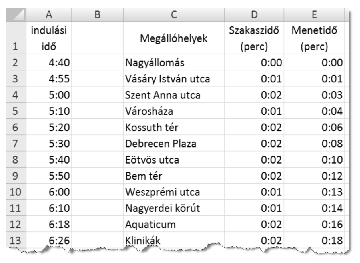
Information based on data in cells B1:B3 and given to the actual passenger should appear in column E (intentionally omitted in the example). Auxiliary computations can be performed, but they, with your corresponding comments, should be visible only to the right of column G.

Cell E1 should contain either the word helyes (= valid) or helytelen (= invalid), according to whether data in B1:B3 are consistent or not. A helytelen message should be displayed, if an invalid station name is entered, or the preferred travel time is after service hours, or if any other inconsistency is detected. You should document these on the sheet where auxiliary computations are done. If a helytelen message has been displayed, further information cells should remain empty.

Cell E2 should contain the earliest exact arrival time of the tram according to the timetable when the passenger can get on the vehicle to reach their destination. (It is hoped that this will be realized in Hungary sometime in the future.)

In cell E3, you should determine the arrival time of the tram to the passenger's destination.

Cells E4 and E5 should contain the number of stations and number of minutes the passenger should travel.

The spreadsheet (i323.xls, i323.ods, ...) together with a short documentation (i323.txt, i323.pdf, ...) also describing your solution, and the name and version number of the spreadsheet application should be submitted in a compressed file (i323.zip).

Downloadable file: menetrend.txt

(10 pont)

solution (in Hungarian), statistics

---

I. 324. In this exercise your task will be to create a presentation illustrating the concept of inversion in geometry. Inversion is discussed, for example, in many online documents, so understanding its simple but elegant mathematics should not pose any difficulties for our contestants.

On your first slide, you should present the notion and basic properties of inversion. On the second slide, an animation should appear showing us how to construct the inverse point of a given one by using only compass. The third slide should represent how to construct the inversion of a circle itself. During your work, you should use the GeoGebra software, capable of displaying the construction process step by step. You should record the GeoGebra animation, or use a suitable presentation software to create an animation from the images of successive construction steps. The next few slides should convince the viewer how effective the method of inversion can be in traditional ruler-and-compass constructions, when only compass is allowed, but not the ruler. Pick one particular geometry problem and illustrate its solution by performing ruler-and-compass construction, and, at the same time, the corresponding construction by using inversion: each step of both constructions should be animated simultaneously on the same slide.

The complete presentation (i324.ppt, i324.odp, ...) together with your GeoGebra files and with a short documentation (i324.txt, i324.pdf, ...) also describing the name and version number of the presentation software should be submitted in a compressed file (i324.zip).

(10 pont)

solution (in Hungarian), statistics

Problems with sign 'S' Deadline expired on June 10, 2013.

---

S. 81. You are going to build a house, where the name of each work phase (e.g., window glazing, installing electrical wiring, wall coating) is known. It is also known for each work phase that they can be started only a certain number of days after another given phase has started (for example, before installing electrical wiring, walls must be built, which takes x days). It is possible to carry out several work phases simultaneously.

Moreover, you should also rent equipment: until the first day of the last work phase (we can suppose that the last work phase lasts for only 1 day). Hence, if the last work phase begins on the day, then we should pay T^.P HUF as a rental fee.

Beside the above, we have to buy also raw materials for each phase. As a simplifying assumption, we suppose that the cost function of the raw materials is a monotone decreasing (more precisely, non-increasing) function of time, being constant on each neighboring time interval. As an example, the cost is 30 HUF between the 1st and 10th days; 20 HUF between the 11th and 20th days; and 15 HUF between the 21st and 40th days.

Write your program that - knowing the dependence of the work phases, the equipment rental fee P, and the cost function for the raw materials for each phase - calculates the minimal cost of building the house provided that the scheduling of the work phases is optimal.

The first line of the standard input contains the number of work phases (), the number of dependencies () between the phases, and the rental fee (0P1000), separated by a space. Then each of the following E lines contains a triplet, say (a_i,b_i,c_i), describing a dependency: phase b_i can be started only c_i days after starting phase a_i (1iE). The next N lines contain the costs of raw materials for each phase in the following format: in each line (corresponding to one phase) the first number is K (1K100), then K pairs, (f_j,v_j), are listed (1jK, 0f_j1000, 1v_j10⁹). Each such pair describes one of the consecutive time intervals: day v_j is the last day of the actual interval when the cost of raw materials is still f_j for the current work phase. The first interval starts on the first day, the next interval starts the next day after the previous interval has ended, and so on.

The only line of the standard output should contain the minimal cost of building the house.

You can suppose that the dependencies are consistent, that is, the house can be built. Raw materials should be bought on the first day of the corresponding work phase. For each phase, the last time interval of the raw material cost function ends on the same day (1D10⁹). The construction of the house can begin no sooner than the first day, and should be finished no later than the day.

In the example, ``Példa bemenet'' is the sample input, while ``Példa kimenet'' is the corresponding output. An explanation to the example is given as follows: starting dates for the work phases in an optimal schedule can be 1, 2, 4, 8 (or 1, 2, 3, 8). Then the cost of raw materials is 3+2+3+3=11, plus 8 HUF rental fee, yielding 19 HUF as a total cost. (If starting dates were 1, 2, 3, 7, then the total cost would be 3+2+3+10+7=25.)

Scoring. You can obtain 1 point for a brief and proper documentation clearly describing your solution. The remaining maximal 9 points for your program can only be obtained if it can solve an arbitrary valid input within 1 second of running time. Partial points of the above 9 points can be obtained if your program can solve test cases within the allotted time only with parameters orders of magnitude smaller than in the maximal inputs (e.g., with smaller N, E, v_j or K values).

The source code (s81.pas, s81.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but together with a short documentation (s81.txt, s81.pdf, ...) - also describing which developer environment to use for compiling, further a brief description of your solution - should be submitted in a compressed file s81.zip.

(10 pont)

solution (in Hungarian), statistics