A KöMaL 2013. októberi informatika feladatai

I-jelű feladatok A beküldési határidő 2013. november 11-én LEJÁRT.

---

I. 328. Egy bűntény felderítése során a detektív sorra hallgatja ki a tanúkat. A detektív segítőjeként az a feladatunk, hogy megállapítsuk, van-e a kijelentések között ellentmondás.

A feladat megoldásához programot készítünk, amelynek természetesen nem mondatokat, hanem az angol ábécé első 10 betűjéből és logikai műveletekből álló kifejezéseket kell feldolgoznia. A logikai kifejezés leírása során a nem, az és, a vagy és az implikáció műveleteket használjuk, amelyeket rendre a ., &, |, > karakterekkel jelöljük. A műveletek végrehajtási sorrendje a matematikában és informatikában szokásos, melyet zárójelezéssel módosíthatunk.

A bemeneti fájlban soronként egy-egy kifejezés van, mindegyik valamelyik tanú által mondott igaz állítás. A kimeneti fájl első sorában annak a sornak a száma van, amelyben szereplő kijelentés ellentmondásban van a korábbiakkal. Ha nincs ellentmondás, az első sorba a 0 kerül.

A program első parancssori argumentuma a bemeneti fájl neve, a második paraméter pedig a kimeneti fájl neve legyen.

Beküldendő a program forráskódja (i328.pas, i328.cpp, ...), valamint a program rövid dokumentációja (i328.txt, i328.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

(10 pont)

megoldás, statisztika

---

I. 329. Egy városnegyedben egyetlen teherautó végzi az üzletek közötti áruszállítást. A városnegyed Manhattan-szerű, mert csak egymásra merőleges utcái vannak.

Az üzletek címjegyzéke és példaként a teherautó egy lehetséges napi útvonala rendelkezésre állnak a honlapunkról elérhető szallitolevel.txt állományban. A címjegyzékben az üzletek sorszáma, a neve és a térkép-koordinátái vannak méterben. A napi útvonal egymás után tartalmazza az üzletek sorszámát. Lehet, hogy egy-egy üzletbe többször is szállítani kell, és a telephelyre is többször visszatérhet a teherautó.

Táblázatkezelő program segítségével oldjuk meg a következő feladatokat, amelyekkel statisztikai adatokat kapunk a napi szállításról:

A megoldás során vegyük figyelembe a következőket:

- Segédszámításokat az M oszloptól jobbra végezhetünk.

- Amennyiben lehetséges, a megoldás során képletet, függvényt, hivatkozást használjunk.

1. Töltsük be a tabulátorokkal tagolt, UTF-8 kódolású szallitolevel.txt szövegfájlt a táblázatkezelőbe az A1-es cellától kezdődően. Munkánkat i329 néven mentsük el a táblázatkezelő alapértelmezett formátumában.

Az A1:D34 tartományban az üzletek címjegyzéke van. Az F2-es cellától lefelé a napi szállításban egymás után felkeresendő üzletek sorszáma írható egymás alá. Ez utóbbiak listája naponta változhat. A teherautó napi útvonala maximum 30 elemből áll.

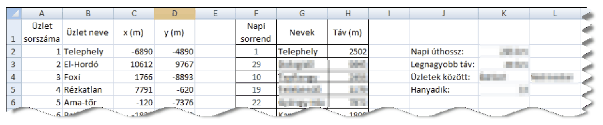
2. Segítsük a sofőr munkáját azzal, hogy a G2:G31 tartományban a szállítási címként szereplő üzletek nevét és a H2:H30 tartományban az egymás utáni üzletek távolságát határozzuk meg. Távolságon a feladatban a Manhattan-távolságot értjük. Az egyik üzlet (x₁,y₁) és valamely másik üzlet (x₂,y₂) Manhattan-távolsága |x₁-x₂|+|y₁-y₂|. Ha a ,,Napi sorrend''-ben üresen maradnak cellák, mert aznap harmincnál kevesebb fuvart kell lebonyolítani, akkor ezek sorában a nevek és a távolságok cellái is üresen jelenjenek meg.

3. A K2-es cellában számítsuk ki, hogy a teherautó hány kilométert tesz meg az adott napon. Az eredményül kapott összeget felfelé kerekítve, egészként, ,,km'' mértékegységgel jelenítsük meg.

4. A K3-as cellában határozzuk meg felfelé kerekítve kilométerben, hogy milyen távol van a napi útvonalban a két legtávolabbi üzlet. A K4-es és az L4-es cellában adjuk meg ennek a két üzletnek a nevét is.

5. A K5-ös cellában jelenítsük meg, hogy a leghosszabb útszakasz hányadik a napi útitervben.

6. A minta alapján végezzük el a szükséges cellaformázásokat.

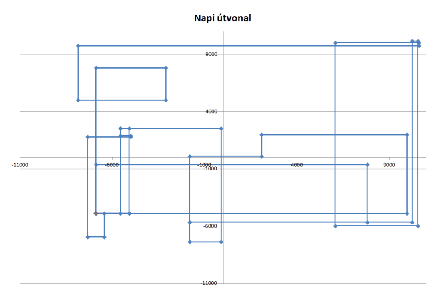
7. A teherautó napi útvonalát diagrammal tegyük szemléletessé. Az XY-diagramon jelenítsük meg az útvonalat úgy, hogy a merőleges fordulások pontjai is látszódjanak. A teherautó két üzlet között úgy közlekedik, hogy először x-irányban elmegy a megfelelő kereszteződésig, és onnantól erre merőleges irányban mozog tovább. A diagram rajzolását segédszámításokkal, segédkoordináták felvételével készítsük elő.

8. Az XY-diagramot külön munkalapra tegyük. Az üzletek és a fordulások helyét ábrázoló pontokat kössük össze. Egyéb beállítások:

- A diagramra ne tegyünk jelmagyarázatot.

- A diagram címe: ,,Napi útvonal''.

- A könnyebb értékleolvasás miatt a függőleges és vízszintes skálát 11000 méterig állítsuk.

- Keressük meg a diagramon a ,,Telephely'' helyét ábrázoló pontot, és ennek színét állítsuk be a többitől eltérőre.

Beküldendő a táblázatkezelő munkafüzet (i329.xls, i329.ods, ...), illetve egy rövid dokumentáció (i329.txt, i329.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.

Értékelés: az első hat feladat helyes megoldása 7 pontot, az utolsó két - az érettségi szintjét meghaladó feladat - megoldása 3 pontot ér.

Letölthető fájl: szallito.txt

(10 pont)

megoldás, statisztika

---

I. 330. Az infografika fénykép, rajz és szöveg együttes alkalmazása, amely több mint egy fénykép, összetettebb, mint egy rajz és informatívabb, mint maga a szöveg. Az infografika célja minden esetben az információközlés. A jó infografika figyelemfelkeltő, informatív, közérthető. Az alábbi címen több jól sikerült infografikát találhatunk: http://www.1stwebdesigner.com/inspiration/beautiful-infographics/

Az iskolák működését szabályozó törvényeket és rendeleteket a helyben készített pedagógiai program kiegészíti. Ez a dokumentum szabja meg többek között azt, hogy az egyes osztályok a tantárgyakat milyen óraszámban tanulják.

Azt a feladatot kaptuk, hogy az iskolát ajánló dokumentumban infografikán mutassuk be a képzési rendszert. Nem szükséges minden részletre kitérni. Szorítkozhatunk akár egy osztálytípusra, készíthetünk évfolyamonkénti bontást, kiemelhetjük a kötelezőnél nagyobb óraszámokat, de választhatunk más szempontokat is. A lényeg a minél ötletesebb, látványosabb hatás.

Beküldendő tömörített állományban (i330.zip) a kész infografika és egy rövid dokumentáció (i330.txt, i330.pdf, ...), amely tartalmazza a felhasznált szoftvereszközöket és iskolád pedagógiai programjának url-jét.

(10 pont)

megoldás, statisztika

S-jelű feladatok A beküldési határidő 2013. november 11-én LEJÁRT.

---

S. 83. Van egy N×M-es tábla csokink (N sor, M oszlop), amit szét szeretnénk osztani N×M gyereknek. Mivel ezt igazságosan szeretnénk megtenni, így mindenkinek pontosan egy ,,kocka'' csokit fogunk adni. Ehhez fel kell tördelnünk a tábla csokit. Ezt úgy végezzük, hogy kezdetben letesszük az asztalra, majd egy-egy törés után minden darabot az eredeti helyére teszünk vissza. Minden törésnek van valami költsége: az i-edik és az i+1-edik oszlop közti törés költsége o_i, a j-edik és j+1-edik sor közti törés költsége s_j. Ez azt jelenti, hogy ha van egy csokidarab az asztalon, akkor annak a törése kerül ennyibe. Ezzel az asztalon lévő többi különálló csokidarabon nem törtünk. A törések során minden csokidarab a helyén marad, nem helyezhetjük át oda, ahol olcsóbb lenne törni, egymásra sem tehetjük őket, hogy ,,egyszerre'' törjük. Csak a tábla oldalaival párhuzamos vonal mentén törhetjük a csokit.

A szabályoknak megfelelően minél olcsóbban szeretnénk 1×1-es ,,kockákra'' osztani a csokit. Adja meg a program, hogy mi ez a minimális költség.

A program olvassa be a standard input első sorából M-et és N-et (), majd a következő M-1 sorból az o_i egészeket, végül a következő N-1 sorból az s_i egészeket, és írja a standard output első, és egyetlen sorába a minimális törési összköltséget.

Magyarázat: Ha először a sorok, majd az oszlopok mentén törünk, akkor

s₁+s₂+s₃+4^.(o₁+o₂+o₃+o₄+o₅)=7+4^.11=51

lenne a törési költség. Ennél lehet olcsóbban is.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Részpontszámok a következőkre kaphatóak:

- a program N,M5-re megoldást ad;

- a program N,M50-re megoldást ad;

- a program N,M500-ra megoldást ad;

- a program N,M1000-re megoldást ad.

Beküldendő egy tömörített s83.zip állományban a program forráskódja (s83.pas, s83.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s83.txt, s78.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika