KöMaL Problems in Informatics, April 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on May 12, 2014. |
I. 346. The present exercise is similar to our earlier Problem I. 343. Now we again have an \(\displaystyle N\times N\) (\(\displaystyle 4\le N\le 50\)) board, and each cell of the board is either empty or has some color. When the board is in its vertical position, the colored squares try to occupy the lowest possible empty positions due to the gravitational force. This time however the board also contains some preset and fixed obstacles that block the way of the sliding colored squares. Empty squares are denoted by a . character, the colored squares can be either red (denoted by P), blue (K) or green (Z), while a fixed obstacle is denoted by A. The board is surrounded by a border preventing the colored squares from falling out. In this exercise the board can be rotated only to the right. After the rotation, the colored squares will again slide to the lowest free positions, and they will stay on top of each other. We are now interested in the mixing effect due to the presence of the obstacles and the rotations. In the example, ``indulás'' is the starting position, and ``1. forgatás után'' is the state of the board after the first right turn.
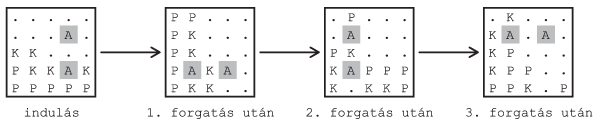
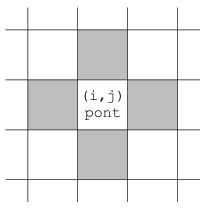
In the starting position and after each rotation you should determine the number of colored squares having at least two neighbors of the same color. The figure shows that a square \(\displaystyle (i,j)\) has by definition 4 neighbors.
Create your program i346 to simulate the rotation of the board and the mixing of the colors.
The first command line argument to your program is the name of the data file describing the board. The first line of the file contains the board size \(\displaystyle N\) (\(\displaystyle 4\le N\le 50\)) and the number of rotations \(\displaystyle K\) (\(\displaystyle 1\le K\le 100\)). The following \(\displaystyle N\) lines contain the initial cell content of the board.
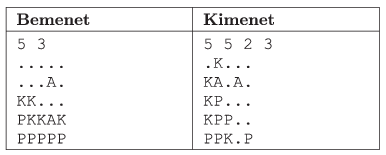
The second command line argument to your program is the name of the output file. The first line of this file should contain the number of colored squares having at least two neighbors of the same color after each rotation; these numbers should be separated by a space. The remaining \(\displaystyle N\) lines of the output file should describe the content of each cell of the board after the last rotation; each line of the file corresponds to a row of the board. In the example, ``Bemenet'' is an input, while ``Kimenet'' is the corresponding output.
The source code (i346.pas, i346.cpp, ...) of your program and a brief documentation (i346.txt, i346.pdf, ...) of your solution should be submitted, also specifying the name of the developer environment to use for compiling your source.
(10 pont)
solution (in Hungarian), statistics
I. 347. A certain table tennis club organized a Table Tennis Doubles Tournament of Luck over the weekend with the following rules. Each participant draws a number at the beginning, and during the tournament they are assigned to pairs according to these numbers. Both pairs of a turn are drawn just before the start of the play. A player and their actual partner always play two sets (not necessarily two won sets) with their randomly selected opponents. A player cannot play twice with the same teammate and against the same opponents. The whole tournament was based on luck: if a player had luck, they could play with a strong partner. If not, they could also win, since there are more opportunities in a doubles game. During the game, both teammates score a point for each won service, irrespective of whether they won the game or not. A player's points were simply added at the end of the tournament. The champion is who scored the most points. Due to space and time limitations, the total number of players was limited to 44, and finally every player played 7 games. A set was played until 11 points were won.
1. Create a new database named lutri to evaluate the game results. The three given data tables (jatekos.txt, par.txt, merkozes.txt) should be imported into the database by using the file names as table names (jatekos, par, merkozes, meaning ``player'', ``pair'' and ``game''). These files are UTF-8 encoded and tabulator-separated text files, with their first lines containing the field names. After creating the tables, the appropriate types should be set, and the appropriate fields should be marked as keys.
Tables:

Queries in the following tasks should be saved by using the names given in parentheses. Your solution should contain only the requested fields or expressions, and no others. In the solution we can assume that each player has a different name.
2. Create a query to display first the names of the female players, then those of the male players, sorted according to their birth years. The list should contain the names and the birth years. Players having the same birth year should be sored alphabetically. 2nevezok)
3. Make a query to determine the number of games in which the same pair won both sets. (3erosebb)
4. Create a report to list the player named Forrai Laura and her partners for each game. The report should be prepared by using a query. (4forraipartnerei)
5. By using a query, display the members of the pairs who won one of their sets with 0 points. (5tuleros)
6. By using a query, give the points for each game of the oldest player. (6legidosebb)
7. By using a query, determine the first 10 winners and their number of points. (7elso10)
8. List by a query for each player the number of sets won. In the list, the names and the number of won sets should appear in a decreasing order according to this last quantity. (8jatszmagyoztes)
The database (lutri.odb, lutri.mdb) and a short documentation (i347.txt, i347.pdf) should be submitted, also specifying the name and version number of the database manager, in a compressed file (i347.zip). The data tables to be imported into the database can be downloaded from our web page: jatekos.txt, par.txt and merkozes.txt
Downloadable files:
(10 pont)
solution (in Hungarian), statistics
I. 348. Your task is to create a one-person game that can be played offline. The description of the game is given below.
The game takes place on a closed board of \(\displaystyle n\times n\) unit squares (\(\displaystyle n=7, \dots, 10\)). When the game starts, the program draws \(\displaystyle k\) horizontal and \(\displaystyle k\) vertical (\(\displaystyle n< k< 2n\)) sides of some squares such that the corresponding area is connected (a certain area is connected if every square can be reached within the area from any other square). The player's task is to draw (by clicking) as many new walls as possible such that the area is still connected.
The game ends when the connectedness is violated, or the player does not click within 5 seconds.
Walls drawn by the program and the player should be different. At the end your program should display the number of built walls and the total playing time.
The source code file(s) should be submitted in a compressed file (i348.zip), together with a short documentation (i348.pdf) consisting of a brief description of your solution and specifying the name of the developer environment to compile your source.
(10 pont)
 |
Problems with sign 'S'Deadline expired on May 12, 2014. |
S. 89. A school has \(\displaystyle N\) students, standing in a big circle on the last school day before vacation. Each student should be given a certain number of chocolate bars: the number of chocolate bars is equal to the number of reward points (denoted by \(\displaystyle a_i\)) they had collected during the school year. Unfortunately, due to a flaw in the logistic system, they mixed up these numbers. So the chocolate bars were just somehow distributed along the circle in \(\displaystyle N\) heaps: the \(\displaystyle i^\mathrm{th}\) heap contained \(\displaystyle b_i\) bars. Although the total number of distributed chocolate bars was correct, yet the probability that each student would get the correct number of bars this way is quite low. Therefore one student reorders the heap so that the \(\displaystyle i^\mathrm{th}\) heap contains \(\displaystyle a_i\) bars. During this reordering process, he can grasp some bars from a heap and can put them into another, arbitrary heap. The number of seconds needed to relocate a particular chocolate bar is equal to the distance of the corresponding two heaps along the perimeter. By performing such steps, the chocolate bars are finally rearranged as originally planned. The goal is to do this as quickly as possible. Your task is to give the minimal time needed to complete the redistribution.
Bounds:
\(\displaystyle \bullet\) \(\displaystyle 1 \le N \le 100\;000\);
\(\displaystyle \bullet\) \(\displaystyle 1 \le a_i, b_i \le 1000\).
Your program should read the value of \(\displaystyle N\) from the first line of the standard input, then the integers \(\displaystyle a_i\), \(\displaystyle b_i\) (separated by a space) from the following \(\displaystyle N\) lines. Your program should write the necessary minimal time to properly hand out the chocolate bars to the first and only line of the standard output.
In the example, ``Példa bemenet'' is a possible input and ``Példa kimenet'' is the corresponding output.

Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time. Partial points can be obtained if your program yields a solution
\(\displaystyle \bullet\) for \(\displaystyle N\le 200\), or
\(\displaystyle \bullet\) for \(\displaystyle N\le 5000\).
The source code (s89.pas, s89.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s89.txt, s89.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s89.zip.
(10 pont)
$Var(Body)
Upload your solutions above
