A KöMaL 2014. áprilisi informatika feladatai

I-jelű feladatok A beküldési határidő 2014. május 12-én LEJÁRT.

---

I. 346. Egy \(\displaystyle N\times N\)-es (\(\displaystyle 4\le N\le 50\)) tábla cellái üres vagy színes négyzetek az I. 343. feladatban leírtakhoz hasonlóan. A táblát függőlegesre állítva a színes négyzetek a legalacsonyabb üres helyig egymásra vagy az előre behelyezett és rögzített akadályig csúsznak a gravitáció miatt. Háromféle (piros, kék és zöld színű) négyzet lehetséges, amelyeket P, K és Z betűk jelölnek. Az üres cellát a . karakter, a rögzített helyű akadályokat az A betű jelöli. A táblát szegély veszi körbe, ami megakadályozza, hogy a színes négyzetek kiessenek.

A táblát csak jobbra lehet forgatni. A forgatás hatására a színes négyzetek újra a legalacsonyabb szabad cellába csúsznak, de egymásról nem esnek le. A rögzített akadályok és a forgatás keverő hatását vizsgáljuk.

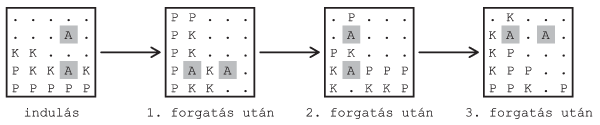
Számoljuk meg induláskor és forgatás után, hogy hány olyan színes négyzet van a táblában, amelynek egynél több vele azonos színű szomszédja van. Szomszéd cellákon most négyet értünk, az ábrának megfelelően.

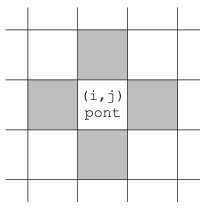
Készítsünk programot i346 néven, amely a tábla forgatását, a színek keverését szimulálja.

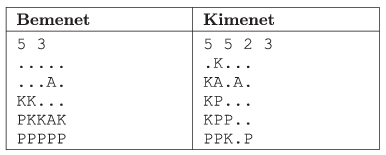
A program első parancssori argumentuma a táblát leíró adatállomány neve legyen. A fájl első sora \(\displaystyle N\) (\(\displaystyle 4\le N\le 50\)) a tábla méretét és \(\displaystyle K\) (\(\displaystyle 1\le K\le 100\)) a forgatások számát adja meg. Az ezt követő \(\displaystyle N\) sor a tábla indulás előtti cellánkénti tartalmát adja meg.

A parancssor második argumentumaként megadott kimeneti állomány első sorában forgatásonként az olyan színes négyzetek számát írjuk ki szóközzel elválasztva, amelyeknek egynél több velük azonos színű szomszédjuk van. Az ezt követő \(\displaystyle N\) sorban a legutolsó forgatás utáni tábla tartalmát adjuk meg soronként.

Beküldendő a program forráskódja (i346.pas, i346.cpp, ...) és rövid dokumentációja (i346.txt, i346.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

---

I. 347. Az egyik asztalitenisz klub Lutri Páros Pingpong Versenyt szervezett egy hétvégi napra. A verseny szabályai a következők voltak:

A helyszínen minden nevező húzott egy számot, és a verseny alatt a játékosokat a kihúzott számok alapján sorsolták. Minden forduló páros partnerét és ellenfelét közvetlenül a játék előtt sorsolták ki. A játékosok az épp aktuális partnerükkel két szettet (nem két nyertet) játszottak a véletlenszerűen kihúzott alkalmi párossal. Kétszer ugyanazt a partnert és ugyanazt az ellenfelet nem kaphatták. Az egész verseny lutri volt a játékosok számára. Ha szerencséjük volt, mindig erős partnerrel játszottak, ha nem, akkor is nyerhettek, mert párosban minden lehetséges.

A játék során minden győztes labdamenetért pont járt a páros mindkét tagjának, függetlenül attól, hogy a mérkőzést megnyerték-e, vagy sem. Mindenkinek annyi pontja lett a végére, ahány pontot szerzett a mérkőzések alatt. A legtöbb pontot összegyűjtő játékos lett a bajnok.

A rendelkezésre álló hely és idő miatt az indulók számát 44-ben korlátozták és végül mindenki 7 mérkőzést játszott. A játszmákat 11 nyert pontig játszották.

1. Készítsünk új adatbázist lutri néven az eredmények kiértékeléséhez. A mellékelt három adattáblát (jatekos.txt, par.txt, merkozes.txt) importáljuk az adatbázisba a fájlnévvel azonos táblanéven (jatekos, par, merkozes). Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első soruk a mezőneveket tartalmazzák. A létrehozás során minden táblában állítsuk be a megfelelő típusokat, és jelöljük meg a kulcsnak megadott mezőt.

Táblák:

A következő feladatok megoldásánál a lekérdezéseket a zárójelben olvasható néven mentsük. Ügyeljünk arra, hogy a megoldásban pontosan a kívánt mezők, kifejezések szerepeljenek, felesleges mezőt ne jelenítsünk meg. A megoldás során feltételezhetjük, hogy nincs két azonos nevű személy.

2. Készítsünk lekérdezést, amely először a nők, majd a férfiak nevét jeleníti meg a születési évük sorrendjében. A listában a nevek és a születési évek jelenjenek meg, az azonos évben születtek esetében ábécé sorrendben. (2nevezok)

3. Készítsünk lekérdezést, amely megadja, hogy hány olyan mérkőzés volt, ahol mindkét szettet az egyik páros nyerte. (3erosebb)

4. Készítsünk jelentést, amely Forrai Laura és párjainak nevét kilistázza mérkőzésenként. A jelentés elkészítését lekérdezéssel készítsük elő. (4forraipartnerei)

5. Lekérdezés segítségével jelenítsük meg azon párosok tagjainak nevét, akik valamelyik szettjüket 0-ra nyerték. (5tuleros)

6. Adjuk meg lekérdezés segítségével a legidősebb játékos mérkőzésenkénti pontszámait. (6legidosebb)

7. Határozzuk meg lekérdezés segítségével az első 10 helyezett nevét és pontszámát. (7elso10)

8. Listázzuk ki lekérdezés segítségével játékosonként, hogy hány győztes szettet szereztek. A felsorolásban a nevek és a győztes szettek száma jelenjen meg az utóbbi szerint csökkenő sorrendben. (8jatszmagyoztes)

Beküldendő egy tömörített állományban (i347.zip) az adatbázis (lutri.odb, lutri.mdb), valamint egy rövid dokumentáció (i347.txt, i347.pdf), amelyből kiderül az alkalmazott adatbázis-kezelő neve és verziószáma.

Az adatbázisba importálandó - honlapunkról letölthető - adattáblák: a jatekos.txt, a par.txt és a merkozes.txt

Letöltendő fájlok:

jatekos.txt

merkozes.txt

par.txt

(10 pont)

megoldás, statisztika

---

I. 348. Készítsünk offline játszható egyszemélyes játékot az alábbiaknak megfelelően:

A játék egy \(\displaystyle n\times n\) egységnégyzetből álló (\(\displaystyle n=7\dots 10\)) zárt területen zajlik. A játék indításakor a program vízszintesen és függőlegesen is \(\displaystyle k\) (\(\displaystyle n< k< 2n\)) helyen megrajzolja a területet alkotó négyzetek egy-egy oldalát úgy, hogy a terület összefüggő maradjon. Összefüggőnek tekintjük a területet, ha bármely négyzetről bármely négyzetbe el lehet jutni. A játékos feladata megrajzolni (kattintással) úgy további falakból minél többet, hogy az összefüggőség megmaradjon.

A játéknak vége, ha az összefüggőség nem teljesül vagy a játékos nem tud lépni 5 másodpercen belül.

A felületen megkülönböztethetők legyenek a gép és a játékos által húzott falak. A végén a program jelenítse meg a behúzott falak számát és a felhasznált összes időt.

Beküldendő(k) a program forráskódját alkotó fájl(ok) egy fájlba tömörítve (i348.zip) és rövid dokumentációja (i348.pdf), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

S-jelű feladatok A beküldési határidő 2014. május 12-én LEJÁRT.

---

S. 89. Egy iskolába \(\displaystyle N\) gyerek jár, akik az évzáró alkalmával egy nagy körben álltak fel az iskolaudvaron. Minden gyereknek annyi csokit kell kapnia év végén, amennyi piros pontot évközben gyűjtött, legyenek ezek az \(\displaystyle a_i\) számok. Sajnos a beszállító nem tudta megjegyezni, hogy kinek mennyi csoki jár, így a hozott csoki mennyiséget valahogy letette \(\displaystyle N\) kupacba a körben a gyerekek elé. A \(\displaystyle i\)-edik kupacba \(\displaystyle b_i\) darab csokit került. A beszállító annyi csokit hozott, amennyit a gyerekeknek összesen szét kell osztani, de így valószínűleg kevés gyerek kapna annyit, amennyit megérdemel. Ezért a következőt találták ki: a diákönkormányzat vezetője megpróbálja átrendezni a csokikat úgy, hogy az \(\displaystyle i\)-edik kupacban \(\displaystyle a_i\) darab legyen az átrendezés végén. Ehhez felemelhet egy kupacból néhány csokit, és leteheti egy tetszőleges kupachoz. Egy csoki áthelyezése annyi másodpercbe kerül, amennyi a két kupac távolsága a kör kerületén haladva. Ilyen lépések egymásutánjával fogják úgy átrendezni a csokikat, hogy megfeleljen a kívánalmaknak. Sajnos a rendezgetés miatt csúszik az évzáró, így minél gyorsabban meg kell oldani a problémát. Adjuk meg, hogy legalább mennyi időt vesz igénybe az átrendezés.

Korlátok:

\(\displaystyle \bullet\) \(\displaystyle 1 \le N \le 100\;000\);

\(\displaystyle \bullet\) \(\displaystyle 1 \le a_i, b_i \le 1000\).

A program olvassa be a standard input első sorából \(\displaystyle N\)-et, majd a következő N sorból az \(\displaystyle a_i\), \(\displaystyle b_i\) szóközzel elválasztott egészeket. Írja a standard output első és egyetlen sorába a szükséges minimális csoki átadások idejét.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.

Részpontszámok a következőkre kaphatóak:

\(\displaystyle \bullet\) a program \(\displaystyle N\le 200\)-ra megoldást ad;

\(\displaystyle \bullet\) program \(\displaystyle N\le 5000\)-re megoldást ad.

Beküldendő egy tömörített s89.zip állományban a program forráskódja (s89.pas, s89.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s89.txt, s89.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika