A KöMaL 2014. szeptemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2014. október 10-én LEJÁRT. |
I. 352. Egy \(\displaystyle N\times M\) (\(\displaystyle 2\le N, M\le 50\)) négyzet alakú és egyforma méretű telkekből álló lakótelepen a házak szintjeinek száma \(\displaystyle K\) (\(\displaystyle 1\le K\le 9\)). Minden telekre egy épületet építettek, az épületek minden szintjén egy lakás található.
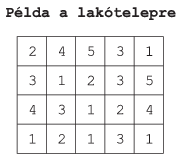
Készítsünk programot i352 néven, amely a lakótelep telep.txt állományban rendelkezésre álló adatait felhasználva néhány kérdésre választ ad.
A képernyőre írást igénylő feladatok eredményének megjelenítése előtt írjuk ki a képernyőre a feladat sorszámát (például: 3. feladat). Ha a felhasználótól kérünk be adatot, akkor jelenítsük meg a képernyőn azt is, hogy milyen adatot várunk. Az ékezetmentes kiírás is elfogadott.
A telep.txt fájl első sora \(\displaystyle N\) és \(\displaystyle M\) értékét adja meg. Az ezt követő \(\displaystyle N\) sor a lakótelep épületeinek szintszámát és végül a lakótelep festéséhez felhasznált színek (például: fehér, sárga, zöld, narancs) egybetűs rövidítését tartalmazza.
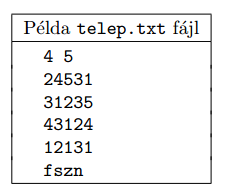
1. Olvassuk be a telep.txt állományban talált adatokat, és azok felhasználásával oldjuk meg a következő feladatokat.
2. Határozzuk meg, hogy a lakótelep lakásainak hány százaléka van \(\displaystyle 1,2,\ldots,9\) szintes épületben. A választ írassuk ki a képernyőre két tizedesjegy pontosan az alábbi formában:
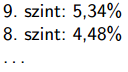
3. Számoljuk meg a ,,körpanorámás'' lakások számát a lakótelepen. A körpanoráma azt jelenti, hogy a lakásból mind a négy oldalán az oldalakra merőleges irányban ki lehet látni a lakótelepről. A kilátást a lakások adott oldalán az abba az irányba épített, velük azonos vagy magasabb más épületrészek eltakarják.
A lakótelep felújításánál az épületeket csíkosra újra festik úgy, hogy minden épületszint más színű lesz a bemenetnél megadott sorrend szerint ismétlődően. A festést a lakótelep térképét tekintve bal felső épületénél kezdik alulról felfelé, és az épületeken soronként balról jobbra haladnak. Egy új épület első szintjének színe az előző épület legfelső szintjének színe után következő lesz.
4. Írassuk ki a felso.txt állományba a legfelső épületszintek színét a következő formában:

5. A lakótelep látványában a festés után fontos a változatosság. Olvassuk be a lakótelep egy épületének pozícióját sor, oszlop formában a bal felső sarokhoz képest, és adjuk meg, hogy van-e olyan szomszédja, amelynek színezése azonos módon kezdődik az első szinttől felfelé függetlenül az épületek magasságától.

6. Az előző beolvasott pozíciójú épület tetejére (következő szintként) egy reklámfeliratot helyeznek el. Írassuk ki, hogy hány lakásból látható ez. Az épületek a velük azonos vagy kisebb más épületrészeket eltakarják és a láthatóság csak sorban és oszlopban értelmezett.
Beküldendő az i352.zip tömörített állományban a program forráskódja (i352.pas, i352.cpp, ...) és rövid dokumentációja (i352.txt, i352.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
Letölthető fájl: telep.txt
(10 pont)
I. 353. Az ,,Egyszámjáték''-ban (Mérő László matematikus és pszichológus találmánya) a játékos tippel egy 1 és 10000 közötti pozitív egész számot. A játék végén megvizsgáljuk a beérkezett számokat, és amelyiket több ember is tippelte, azokat töröljük. A megmaradt számok közül a legkisebb a nyertes.
Például: Ezek a tippek érkeznek egy adott fordulóban: 9, 6, 3, 7, 4, 6, 1, 6, 8, 1, 6, 5, 7, 9, 4, 2. A forduló végén - miután kihagytuk az összes olyan tippet, amit többen is megjátszottak - ezek maradnak: 3, 8, 5. A nyertes a 3-as szám beküldője, mivel a megmaradtak közül ez a legkisebb.
Készítsünk egy játékot kiértékelő táblázatot, amely az e-mailben beküldött tippek alapján megadja a győztes adatait. A tippek.txt forrásállományban rendelkezésre állnak a résztvevő játékosok adatai és tippjei. A játékosokról rendelkezésre álló adatok:
Tipp A játékba beküldött egész szám, értéke \(\displaystyle 1\le \mathsf{tipp}\le 10\;000\);
Név A játékos neve (azonos nevűek is lehetnek);
E-mail A játékos e-mail címe, amely egyedi.
Ha egy e-mail címről a játékba több tippet küldenek be, akkor az először rögzített tippet vesszük csak figyelembe, a többit érvénytelennek tekintjük.
Táblázatkezelő program segítségével oldjuk meg a játék eredményét meghatározó feladatot. A megoldásban saját függvény vagy makró nem használható.
Töltsük be a tabulátorokkal tagolt, UTF-8 kódolású tippek.txt szövegfájlt a táblázatkezelőbe a mintának megfelelően. A megoldásnak elegendő a megadott adatokra jól működnie. Munkánkat i353 néven mentsük el a táblázatkezelő alapértelmezett formátumában.
Alakítsuk ki a minta szerinti táblázatszerkezetet és a D:G oszlop feliratok melletti celláiban adjuk meg kifejezések segítségével a válaszokat. A H oszloptól jobbra segédszámításokat végezhetünk.
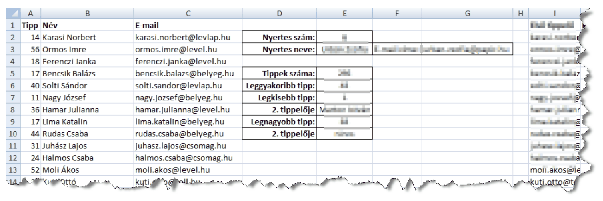
1. Az E2 cellába írjuk ki a nyertes tippet.
2. Az E3 és G3 cellákba írassuk ki a nyertes tippelő nevét és e-mail címét.
A továbbiakban a játékra jellemző értékeket határozzunk meg.
3. Az E5 cellában határozzuk meg a beküldött érvényes tippek számát.
4. Az E6 cellában függvény segítségével határozzuk meg, melyik számot küldték be érvényesen a legtöbben. Ha több ilyen szám van, akkor elegendő az egyiket megadni.
5. Az E7 és E9 cellában függvény segítségével határozzuk meg a legkisebb és legnagyobb érvényes tippet.
6. Az E8 és az E10 cellákban jelenítsük meg a legkisebb, illetve a legnagyobb érvényes tippet időrendben másodikként beküldők nevét. Ha nincs második beküldő, akkor a ,,nincs'' feliratot jelenítsük meg.
7. Formázzuk a táblázatot a minta szerint.
Beküldendő i353.zip néven egy tömörített állományban a táblázatkezelő munkafüzet (i353.xls, i353.ods, ...), illetve egy rövid dokumentáció (i353.txt, i353.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma.
Letölthető fájl: tippek.txt
(10 pont)
I. 354. Ma már minden megtalálható az interneten. Ha valami még nem, az hamarosan megtalálható lesz. Van, aki egy étel elkészítését teszi közzé, más egy műszaki eszköz javítását.
Feladatunk egy vezeték nélküli router beüzemelésének bemutatása egy maximum 5 perc hosszú film formájában. A film az alapállapotú router bekapcsolásától egy tetszőleges vezeték nélküli eszköz biztonságos csatlakoztatásáig tartson. A lényeges adatokat feliratozással emeljük ki. A folyamat bemutatását kísérjük élőbeszéddel. A film során saját belátásunk szerint alkalmazhatunk zenei aláfestést.
A routerrel végzett műveletek és a képernyőtartalom rögzítéséhez és utólagos szerkesztéséhez tetszőleges rögzítő eszközt és programot használhatunk.
Beküldendő egy dokumentum (i354.pdf), amely tartalmazza a router pontos típusát, a feladatban foglaltak megoldása során fölhasznált hardver és szoftver eszközöket, valamint az elkészített filmre mutató hivatkozást.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2014. október 10-én LEJÁRT. |
S. 91. Anna, Béla és Cili kapnak \(\displaystyle N\) (\(\displaystyle 1\le N\le 60\)) ajándékcsomagot. Mindegyik csomagnak tudják az értékét: az \(\displaystyle i\)-edik csomag értéke \(\displaystyle a_i\), ahol \(\displaystyle 1\le a_i\le 100\). El szeretnék osztani egymás között az ajándékokat a lehető legigazságosabban. A legigazságosabb elosztás akkor valósul meg, ha a legnagyobb összértékű csomagokat kapó testvér a lehető legkisebb összértéket kapja. Például, ha a következő csomagokat kapták: 2 4 5 8 9 14 15 20, akkor egy ilyen legigazságosabb szétosztás a következő lehet: Anna: 2 9 15, összesen 26; Béla: 4 8 14, összesen 26; Cili: 5 20, összesen 25. Adjuk meg egy legigazságosabb elosztásban szereplő legnagyobb összértéket (aminek tehát a lehető legkisebbnek kell lennie).
A program olvassa be a standard input első sorából \(\displaystyle N\)-et, majd a következő \(\displaystyle N\) sorból az \(\displaystyle a_i\) szóközzel elválasztott egészeket. Írja a standard output első és egyetlen sorába a szétosztásban a legnagyobb értéket.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Részpontszámok a következőkre kaphatóak:
- a program \(\displaystyle a_i\le 40\)-re megoldást ad;
- a program \(\displaystyle N\le 10\)-re megoldást ad.
Beküldendő egy tömörített s91.zip állományban a program forráskódja (s91.pas, s91.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s91.txt, s91.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

