KöMaL Problems in Mathematics, September 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 10, 2014. |
K. 421. Point \(\displaystyle A\) lies on a diameter in a circle of radius 30 units. The chord drawn through \(\displaystyle A\), perpendicular to the diameter has a length of 18 units. How many chords does the circle have, other than the diameter, that pass through \(\displaystyle A\) and have integer lengths?
(6 pont)
K. 422. Two squares of sides \(\displaystyle a\) and \(\displaystyle b\) are placed next to each other and then cut into five plane figures altogether with two line segments of length \(\displaystyle c\), as shown in the figure. Show that it is possible to build, without gaps or overlaps, a square of side \(\displaystyle c\) out of the five pieces.
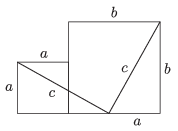
(6 pont)
K. 423. Alex has dinner in the same restaurant every evening. He has Wiener snitzel with fried potatoes and salad. In addition to the total on the bill, he tips the waiter every day. The tip is always equal to the amount that the total of the bill is in excess of 1000 forints (HUF, Hungarian currency). One day, the total on the bill is smaller, since the snitzel is sold at a sales price that is half the normal price (potato and salad prices are not reduced). Examining the bill, Alex observed that the amount of tax to be paid was 135 forints, but he still gave the usual tip of 180 forints to the waiter. What is the full price (including tax) of the snitzel, given that the tax on food is 18% of the net price?
(6 pont)
K. 424. Arrange the whole numbers 1 to 10 in the figure, so that the sum of the numbers along each line segment containing exactly four circles is 23, and the sum of the numbers along each line segment containing exactly three circles is 16. How many different arrangements are there? (Arrangements obtained from each other by rotation or reflection are also considered different.)

(6 pont)
K. 425. We have two machines that transform numbers. If a positive number is fed in such a machine, the output will also be a positive number. Furthermore, the output only depends on the input, that is, if the same number is fed to the same machine again, then the result will also be the same. Our two machines are \(\displaystyle A\) and \(\displaystyle B\). If a number is fed in machine \(\displaystyle A\), and the output is used as input for machine \(\displaystyle B\), then the result will be the square root of the original number. If, on the other hand, a number is fed to machine \(\displaystyle B\) first, and that output is fed to \(\displaystyle A\), then the result will be the square of the original number. If the number 12 is fed to machine \(\displaystyle A\), the output will be 25. What will be the output of machine \(\displaystyle A\) if it is fed the number 144?
(6 pont)
K. 426. A test consists of 100 questions altogether. There are three kinds of questions. True or false questions are worth 0.5 points each, multiple choice questions are 3 points each, and essay questions are 10 points each. The maximum score is 100 points. How many of each type of questions are there on the test?
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 10, 2014. |
C. 1238. What may be the digits \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) in decimal notation if \(\displaystyle \overline{aa\vphantom{b}}^2+\overline{bb}=\overline{cccc\vphantom{b}}\)?
(5 pont)
C. 1239. Find three possible natural numbers \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) (\(\displaystyle x<y<z\)) such that \(\displaystyle 3^x+3^y+3^z=179\;415\).
(5 pont)
C. 1240. Pentagon \(\displaystyle ABCDE\) is obtained by rotating pentagon \(\displaystyle HICBG\) about \(\displaystyle C\), and pentagon \(\displaystyle FGBAE\) is obtained by rotating pentagon \(\displaystyle ABCDE\) about \(\displaystyle E\), as shown in the sketch. The length of line segment \(\displaystyle AB\) is 7 cm.
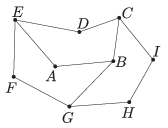
What is the total length of the 11 line segmets?
Based on a German competition problem
(5 pont)
C. 1241. Solve the following equation: \(\displaystyle \left(\frac{x-1}{2} \right)^{2} + \frac12 = \left|\frac{4x}{x+3}\right| - \frac12\).
(5 pont)
C. 1242. The sides of a right-angled triangle are 3, 4, 5. Determine the line that halves both the perimeter and the area of the triangle.
(5 pont)
C. 1243. In the lottery, five numbers are drawn out of the integers 1 to 90. Which is more probable:
\(\displaystyle (a)\) that the numbers drawn form an arithmetic progression? or
\(\displaystyle (b)\) that the largest number drawn is 15?
(5 pont)
C. 1244. The length of each edge of a cuboid is an integer, the length of the diagonal of the cuboid is 65, and the area of the largest diagonal intersection is 1500. Find the lengths of the edges. (A diagonal intersection is an intersection with a plane through a pair of parallel diagonals of two opposite faces.)
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 10, 2014. |
B. 4642. Given that no three of five points in the plane are collinear, prove that there are at most seven acute-angled triangles among the triangles determined by the five points.
(4 pont)
B. 4643. Are there integers \(\displaystyle n\) and \(\displaystyle k\) such that \(\displaystyle n^3-n-1=k^2-k+1\)?
Suggested by K. Williams, Szeged
(3 pont)
B. 4644. Two circles of radius \(\displaystyle r\) are inscribed in a semicircle of radius \(\displaystyle R\) such that the circles touch each other externally and the semicircle internally, as shown in the figure. Determine the radius \(\displaystyle r\).
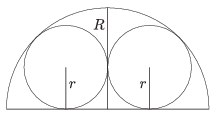
(3 pont)
B. 4645. Let \(\displaystyle H_{1}=\{1, 3, 5, \ldots, 2n-1\}\) and \(\displaystyle H_{2}=\{1+k, 3+k, 5+k, \ldots, 2n-1+k\}\), where \(\displaystyle n\) and \(\displaystyle k\) are any positive integers. Is there an appropriate \(\displaystyle k\) for every \(\displaystyle n\) such that the product of all elements of the set \(\displaystyle H_{1}\cup H_{2}\) is a perfect square?
(5 pont)
B. 4646. For what values of the parameter \(\displaystyle p\) is the inequality \(\displaystyle \left(1+\frac{1}{\sin x}\right)^{3} \ge \frac{p}{\tan^2 x}\) true for all \(\displaystyle 0<x<\frac{\pi}{2}\)?
Suggested by A. Faragó
(4 pont)
B. 4647. Given that 100 closed unit discs, together, cover a different, 101st closed unit disc. Show that there is a disc among the 100 that covers the point on the top of another. (Top means greatest ordinate.)
Suggested by D. Pálvölgyi, Budapest
(6 pont)
B. 4648. The faces of a tetrahedron are congruent triangles with sides of lengths 13, \(\displaystyle \textstyle \sqrt{281}\) and \(\displaystyle 20\) units. Determine the dihedral angle enclosed by two faces.
(5 pont)
B. 4649. Let \(\displaystyle e_1,e_2,\dots,e_n\) denote different lines on the plane, and let \(\displaystyle f\) be a line that is not parallel to any of them. Consider all lines \(\displaystyle f_{\alpha}\) parallel to \(\displaystyle f\). Let \(\displaystyle S_{\alpha}\) be the centre of mass of the points \(\displaystyle f_{\alpha}\cap e_1, f_{\alpha}\cap e_2, \ldots, f_{\alpha}\cap e_n\). Show that the points \(\displaystyle S_{\alpha}\) are collinear.
Suggested by B. Csikós, Budapest
(6 pont)
B. 4650. Is there a function of the form \(\displaystyle f(x)=\frac{ax+b}{cx+d}\) for which \(\displaystyle f(x_1)=x_2\), \(\displaystyle f(x_2)=x_3\), \(\displaystyle f(x_3)=x_4\), \(\displaystyle f(x_4)=x_5\), \(\displaystyle f(x_5)=x_1\) is true if \(\displaystyle x_1,\ldots,x_5\) are appropriate pairwise different real numbers?
Suggested by Gy. Károlyi, Budapest
(6 pont)
 |
Problems with sign 'A'Deadline expired on October 10, 2014. |
A. 620. Arthur and Ben have a chocolate table of size \(\displaystyle k\times n\), they play a game with this chocolate. They alternately eat parts of the chocolate; Arthur is first. In every step, the current player breaks the chocolate table into two rectangular parts along the lines and eats up the smaller part. (If eventually the two pieces are equal, he can choose which part to eat.) The player who first eats a single chocolate square in a step loses, the other player wins.
Determine all pairs \(\displaystyle (k,n)\) for which Arthur has a winning strategy.
based on an Israeli problem
(5 pont)
A. 621. In an acute triangle \(\displaystyle ABC\), the feet of the altitudes are \(\displaystyle A_1\), \(\displaystyle B_1\) and \(\displaystyle C_1\), respectively. The midpoint of the side \(\displaystyle BC\) is \(\displaystyle F\). The circle \(\displaystyle BCB_1C_1\) intersects the line segment \(\displaystyle AA_1\) at point \(\displaystyle D\). Let \(\displaystyle T\) be that point on the line segment \(\displaystyle DF\) for which the line \(\displaystyle BT\) is tangent to the circle \(\displaystyle AB_1C_1\). Let the line segment \(\displaystyle C_1F\) meet the lines \(\displaystyle BD\) and \(\displaystyle BT\) at \(\displaystyle P\) and \(\displaystyle Q\), respectively. Show that the quadrilateral \(\displaystyle DPQT\) has an inscribed circle.
(5 pont)
A. 622. Prove that \(\displaystyle \dfrac{7^{7^{k+1}}+1}{7^{7^{k}}+1}\) is a composite number for every nonnegative integer \(\displaystyle k\).
(5 pont)
Upload your solutions above.
