A KöMaL 2014. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2014. november 10-én LEJÁRT. |
M. 344. A4-es papírlapokból a rövidebb oldalélek (kb. 1 cm-es átfedéssel történő) összeragasztásával papírcsöveket készítünk. A csöveket vízszintes asztallapra állítva, majd tengelyirányú terhelést alkalmazva vizsgáljuk meg, mekkora terhelőerő esetén ,,csuklanak össze''! Hogyan változik a kritikus terhelőerő a papírcső magasságának függvényében?
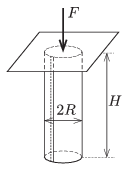
Közli: Vigh Máté, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2014. november 10-én LEJÁRT. |
P. 4660. Mit látunk, ha egy sűrű szövésű tüllfüggönyön, vagy régi típusú (selyemből készült) kinyitott esernyőn át nézünk egy távoli fényforrást?
Közli: Radnai Gyula, Budapest
(3 pont)
P. 4661. Két egyenes, egymásra merőleges útpálya kereszteződése felé egy személyautó és egy teherautó közeledik. A személyautó vonatkoztatási rendszerében a másik úton haladó teherautó sebességének nagysága 90 km/h. A személygépkocsi sebességmérője 72 km/h-t mutat. A mérés pillanatában a teherautó 600 m-re, a személyautó 800 m-re van az útkereszteződéstől. Melyik ér hamarabb a kereszteződéshez, ha mindkettő egyenletesen halad?
Közli: Szombathy Miklós, Eger
(4 pont)
P. 4662. Labdarúgó mérkőzésen a kapus kirúgáshoz készülődik. A rúgás \(\displaystyle \Delta t=0{,}01\) s ideig tart, ezalatt a kapus \(\displaystyle F=850\) N átlagos erővel rúg bele a földön lévő labdába. Ha nem lenne közegellenállás, akkor az elrúgott labda \(\displaystyle t=3\) s múlva, \(\displaystyle \ell=45\) m-rel odébb érne újra talajt.
\(\displaystyle a)\) Legfeljebb milyen magasra jutna fel ekkor a labda?
\(\displaystyle b)\) A labdarúgás hivatalos szabályai szerint a labda tömege 410 g és 450 g között lehet. Szabályosan zajlik-e a mérkőzés?
Közli: Béda Ármin, Garay J. Gimn., Szekszárd
(4 pont)
P. 4663. Egy \(\displaystyle M\) tömegű merev rúd a harmadoló pontján átmenő vízszintes tengely körül foroghat. A tengelyhez közelebbi végéhez \(\displaystyle m\) tömegű, pontszerű testet, a másik végéhez elhanyagolható tömegű serpenyőt rögzítettünk. A rúd vízszintes egyensúlyi helyzetben áll.
Mekkora sebességgel indul el a \(\displaystyle m\) tömegű test, ha a serpenyőbe egy másik, ugyancsak \(\displaystyle m\) tömegű testet ejtünk \(\displaystyle h\) magasságból? A leejtett test benne marad a serpenyőben. A súrlódás elhanyagolható.
Közli: Kobzos Ferenc, Dunaújváros
(5 pont)
P. 4664. Tompkins úr (George Gamow: Tompkins úr kalandjai a fizikával c. könyvének főszereplője) álmában Furcsavilágban járt, ahol a fizika törvényei majdnem ugyanazok, mint a nálunk, ,,csupán'' a tömegvonzás tér el a megszokott Newton-törvénytől. Reggel felébredve Tompkins úr visszaemlékezett, hogy Furcsavilág egyetlen ,,Napja'' körül számos bolygó kering, és ezekre három ,,Kepler-törvény'' érvényes:
1. A bolygók pályája ellipszis, és annak középpontjában van a Nap.
2. A bolygók vezérsugara a mozgás során ...(a folytatást sajnos elfelejtette Tompkins úr).
3. Mindegyik bolygó keringési ideje (az ellipszis kis- és nagytengelyének hosszától függetlenül) ugyanakkora.
Vajon hogy néz ki a furcsavilági fizikakönyvekben a gravitáció törvénye, és mit állít a második ,,Kepler-törvény''?
Közli: Gnädig Péter, Vácduka
(5 pont)
P. 4665. Az ábrán látható függőleges hengerben a dugattyú alatt normál állapotú levegő van. A dugattyú súrlódás nélkül mozoghat, tömege megegyezik az állócsiga másik oldalán levő serpenyő tömegével. Mikor mozdul el jobban a dugattyú, ha a serpenyőbe, vagy a dugattyúra szórunk rá ugyanannyi homokot? (Feltehetjük, hogy a hőmérséklet állandó marad.)
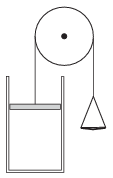
Varga István (1952-2007) feladata
(4 pont)
P. 4666. Hogyan halad tovább a lencsén való áthaladás után az a fénysugár, amelyik egy szórólencse túloldali ,,kétszeres'' fókusza felé tart?
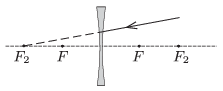
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4667. Szabályos tetraéder csúcspontjaiban azonos előjelű és egyaránt \(\displaystyle Q\) nagyságú ponttöltések helyezkednek el. Mekkora nagyságú, ellentétes előjelű ponttöltést kell elhelyezni a tetraéder közepén, hogy a töltésekre ható eredő elektrosztatikus erő zérus legyen? Mekkora a töltésrendszer kölcsönhatási energiája?
Közli: Tornyos Tivadar Eörs, Budapest
(5 pont)
P. 4668. Konstantánból és krómnikkelből készült huzalok keresztmetszete egyaránt \(\displaystyle 1 ~\rm{mm}^2\). Adjunk becslést arra vonatkozóan, hogy mekkora hőmérsékletűre melegednek fel a légritkított üvegcsőben lévő huzalok (külön-külön), ha rajtuk 1 A erősségű áram folyik! (A környezet hőmérséklete \(\displaystyle 20 ^\circ\)C.)
Közli: Simon Péter, Pécs
(5 pont)
P. 4669. Az urán-238 izotóp \(\displaystyle \alpha\)-bomló, felezési ideje 4,5 milliárd év. Hány atomból álló urántömb esetén bomlik el átlagosan egyetlen atommag
\(\displaystyle a)\) másodpercenként;
\(\displaystyle b)\) óránként;
\(\displaystyle c)\) naponta;
\(\displaystyle d)\) évente?
Közli: Vass Miklós, Budapest
(4 pont)
P. 4670. Függőleges tengelyű, \(\displaystyle \ell=2\) m hosszú, egyrétegű egyenes tekercs átmérője \(\displaystyle D=2\) cm, menetszáma \(\displaystyle N=2000\), benne \(\displaystyle I=10\) A erősségű egyenáram folyik felfelé. (Az áramkör a tekercstől messze záródik.) A tekercs tengelye felé, arra merőleges irányban \(\displaystyle v=2{,}5\cdot10^6\) m/s sebességű elektronokat indítunk. Mekkora az elektronok pályájának görbületi sugara abban a pontban, amelyben az elektronok már \(\displaystyle d=2\) cm-re megközelítették a tekercs meneteit?
Közli: Holics László, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

