A KöMaL 2014. decemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2015. január 12-én LEJÁRT. |
I. 361. A korong lövés nevű játékot egy ember játssza egy \(\displaystyle N\) csúcsú egyszerű gráfon (\(\displaystyle 1\le N\le 20\)). A játék a következőképp néz ki: a gráf minden csúcsán van néhány korong. Egy lépésben a játékos fog egy tetszőleges csúcsot, és ha azon legalább annyi korong van, mint a csúcs szomszédainak száma (azon csúcsok, melyekkel éllel van összekötve), akkor minden szomszédnak ad egy-egy korongot. Akkor nyer a játékos, ha már nem tud ilyen lépést végrehajtani. Adjuk meg, hogy tud-e nyerni egy bizonyos alapállásból a játékos.
Segítség: ha tud nyerni a játékos, akkor bármilyen sorrendben választhatja a csúcsokat, amikkel lép, előbb-utóbb véget ér a játék. Ezt használjuk fel. Továbbá könnyítésképpen, ha ezzel a módszerrel 1000 lépés alatt nem fejeződik be a játék, akkor írjuk ki azt, hogy NEM tud nyerni.
A program a standard bemenet első sorából olvassa be az \(\displaystyle N\) és \(\displaystyle M\) (élek száma) számokat. A következő \(\displaystyle N\) sorban a gráf egyes csúcsain lévő korongok számát, majd a következő \(\displaystyle M\) sorból a gráf leírását: minden sorban egy \(\displaystyle a\) és egy \(\displaystyle b\) szám szerepel, ami azt jelenti, hogy az \(\displaystyle a\) csúcs szomszédja \(\displaystyle b\), és a \(\displaystyle b\) csúcs szomszédja \(\displaystyle a\). A program írja ki a standard output első sorába a NEM szót, amennyiben a segítségben leírt módszerrel 1000 lépés alatt nem fejeződik be a játék. Ha befejeződik, akkor az IGEN szót, és az alatta lévő \(\displaystyle N\) sorban pedig a végállapotban az egyes csúcsokon lévő számokat a bemenet sorrendjében.

Beküldendő egy tömörített i361.zip állományban a program forráskódja (i361.pas, i361.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (i361.txt, i361.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
I. 362. Adott egy játék, amely \(\displaystyle L~(\le 6)\) darab lámpából és a rendszert vezérlő \(\displaystyle G~(\le 6)\) darab gombból áll. A lámpákba egy számláló van beépítve. Az \(\displaystyle i\)-edik lámpa a számláló \(\displaystyle S_{i}\) értékének elérésekor ellenkezőjére változik, a számláló értéke pedig 0 lesz. A \(\displaystyle j\)-edik gomb megnyomásával mindig ugyanazon lámpák számlálóinak értékét növeljük eggyel. Minden lámpát legalább egy gomb vezérel és minden gomb legalább egy lámpát vezérel.
A rendszer működését táblázatkezelő program segítségével szimulálhatjuk.
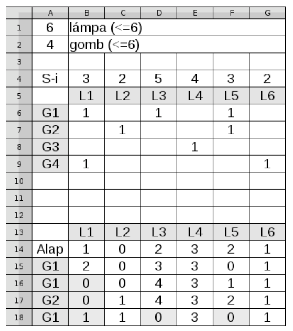
A táblázatot a mintának megfelelően, az alábbiak szerint alakítjuk ki:
\(\displaystyle \bullet\) az A1, A2 cellába bejegyezzük a lámpák és gombok számát;
\(\displaystyle \bullet\) az 5. és a 13. sorban az oszlopfej tartalma a minta szerint csak azokban a cellákban jelenik meg, amelyik lámpa létezik;
\(\displaystyle \bullet\) az A oszlopban a 6. sortól kezdődően a sorfej csak azon cellákban jelenik meg, amely gomb létezik;
\(\displaystyle \bullet\) a 4. sorba bejegyezzük, hogy az egyes lámpák hányadik gombnyomásra váltanak át;
\(\displaystyle \bullet\) a B6 cellától kezdődő tartomány celláiba bejegyezzük, hogy milyen kapcsolat van a gombok és lámpák között;
\(\displaystyle \bullet\) a 14. sorban feltüntetjük a rendszer alapállapotát (a lámpák számlálóinak értékét) - úgy tekintjük, hogy kezdetben a lámpák egyike sem világít;
\(\displaystyle \bullet\) az A15-ös cellától kezdődően soronként beírva egy-egy gomb sorszámát az adott sorban megjelenik a lámpák számlálóinak állása, valamint a szöveg vagy háttérszín jelzi, hogy a lámpa ég vagy sem.
A táblázat készítése során feltételes formázás és függvények használatával érjük el, hogy csak a szükséges cellákban látszódjék érték; felismerhető legyen a hibásan kitöltött vagy hiányzó tartalmú cella (A1:A2, B4:G4, A15:A114, B6:G11). A táblázatot legalább 100 gombnyomásra kell felkészíteni. (A feltételes formázás nem érettségi követelmény.)
A megoldáshoz makró nem, de tetszőleges számú segédcella használható a H oszloptól jobbra.
Beküldendő egy tömörített i362.zip állományban a megoldás rövid leírása (i362.txt, i362.pdf), amely tartalmazza a használt táblázatkezelő program nevét és verzióját, valamint a szimulációt tartalmazó táblázatot (i362.xlsx, i362.ods, ...).
(10 pont)
I. 363. Kisgyerekként sokszor játszottam a rókák és a nyúl játékot. A sakktáblán játszható játék meglehetősen egyszerű és gyors lefolyású. Az egyik játékos a rókákat, a másik a nyulat irányítja. A játék a sakktábla világos mezőin zajlik. A tábla alsó sorának mezőire felállítunk négy egyforma sötét bábut -- a rókákat. A nyulat jelképező világos bábu kezdeti helyét az azt irányító játékos szabadon választja meg a felső sor mezői közül. A játékosok felváltva lépnek átlósan egy szabad szomszédos mezőre. A játék a rókák egyikének lépésével kezdődik. A róka mindig csak felfelé léphet, a nyúl lépését semmi nem korlátozza. A rókák nyernek, ha a nyúl már nem tud lépni. A nyúl nyer, ha a rókák mögé került.
Készítsük el a fenti játék offline is játszható változatát. A program ügyeljen a szabályok betartására. A játék menetét egy külön ablakban rögzítsük, ahonnan a játék végén ki tudjuk másolni. A programnak képesnek kell lennie egy korábban rögzített játék animációként való, jól követhető lejátszására is. Ebben az esetben nem kell vizsgálni a lejegyzés helyességét.
A megoldást tetszőleges programozási eszközzel elkészíthetjük. Ügyeljünk a szép megjelenésre és a könnyű használhatóságra. Az animált megjelenítés miatt a szöveges felületet használó programokat nem tekintjük teljes értékű megoldásnak.
Beküldendő egy tömörített i363.zip állományban a megoldás leírása (i363.pdf), amely tartalmazza megoldás lényeges lépéseinek ismertetése mellett a játék lejegyzési módjának leírását, valamint a program forrásnyelvi változata és a fordításához és működéséhez szükséges fájlok.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2015. január 12-én LEJÁRT. |
S. 94. Egy állatkísérlet során a kutatók arra lettek figyelmesek, hogy ha túl sok állat léphet egymással kapcsolatba, akkor pontatlan lesz a kísérlet. Jelenleg egy \(\displaystyle N\times N\)-es négyzet alakú mezőn (\(\displaystyle 2\le N\le 17\)) túl sok állat tartózkodik. Szeretnénk \(\displaystyle K\) darab (\(\displaystyle 1\le K\le 2N-2\)) kerítést építeni nekik, hogy el legyenek különítve. Egy kerítés párhuzamos a mező valamelyik szélével, és attól egész távolságra halad. Továbbá a teljes négyzeten keresztül kell haladnia (azaz nem lehet vége egy kerítésnek a négyzet belsejében). Ilyen feltételek mellett szeretnénk minimalizálni az összefüggő részeken lévő állatok maximális számát.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle K\)-t (\(\displaystyle 2\le N\le 17\), \(\displaystyle 1\le K\le 2N-2\)), majd a következő \(\displaystyle N\) sorból soronként \(\displaystyle N\) egész számot, melyek jelentése: az adott sorban az adott egységnégyzetben ennyi állat tartózkodik. Írjuk a standard output első és egyetlen sorába a lehető legjobb kerítésépítés mellett a legtöbb állat számát, melyek egymástól nincsenek elkerítve.
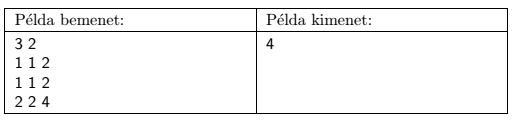
Magyarázat: Két kerítést kell építenünk, méghozzá a 2. és 3. oszlop, és a 2. és 3. sor között érdemes. Ekkor a bal felső részben \(\displaystyle 1+1+1+1=4\) állat lesz, a jobb felsőben \(\displaystyle 2+2=4\), a bal alsóban is \(\displaystyle 2+2=4\), és a jobb alsóban is 4 állat lesz, így 4-et írunk ki.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített s94.zip állományban a program forráskódja (s94.pas, s94.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s94.txt, s94.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

