KöMaL Problems in Physics, January 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 10, 2015. |
M. 347. Fix a wooden skewer to the rim of the table. Gradually load its free end, or hang a spring balance to it. Measure the torque \(\displaystyle M\) needed to break the skewer, and the work \(\displaystyle W\) done by the load. Will the measured data change if the length \(\displaystyle \ell\) of that part of the skewer which sticks out of the table is halved?
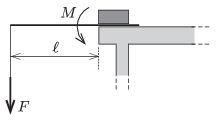
(6 pont)
 |
Problems with sign 'P'Deadline expired on March 10, 2015. |
P. 4693. What is the temperature measured in Kelvins at which a mercury-in-glass thermometer reads the same value in Celsius and in Fahrenheit scale, and what is this same value?
(3 pont)
P. 4694. \(\displaystyle a)\) What is the amount of water in grams in the air of a room of volume 60 m\(\displaystyle {}^3\) at a temperature of \(\displaystyle 25~{}^\circ\)C, if the relative humidity is 50%?
\(\displaystyle b)\) To what per cent value does the relative humidity of the room increase if by the next morning the temperature of the room have decreased to \(\displaystyle 20~{}^\circ\)C? (The windows are closed and well sealed.)
\(\displaystyle c)\) What is the relative humidity of the same sample of air at a temperature of \(\displaystyle 10~{}^\circ\)C?
(4 pont)
P. 4695. There is a 1 cm long operating electrical filament at a distance of 10 cm from a lens of optical power of 5 dioptres. The filament is perpendicular to the principal axis of the lens. A plane mirror, facing towards the lens, is placed to the other side of the lens, 20 cm from it. The mirror is also perpendicular to the principal axis of the lens. Where are the images of the filament and what is their size?
(4 pont)
P. 4696. Disc shaped tablets of diameter 8 mm and of height 4 mm are falling to the tabletop from a small height. Suppose that all directions have the same probability and the tablets do not bounce back from the tabletop. What percentage of the tablets arrive at the table in ``rollable'' position?
(4 pont)
P. 4697. In an article of a newspaper the following was written: ``An electric racing car reaches a hundred in three seconds, its maximum speed is 220 km/h and its power rating is 268 horsepower.'' What may the mass of the car be?
(4 pont)
P. 4698. One end of a thread of length \(\displaystyle \ell\) is attached to a heavy iron ball, whilst the other end of the thread a feather is fixed, and the ball is projected in the horizontal direction. The ball flies through the metal ring shown in the figure. How long does it take for the thread to pass the metal ring?
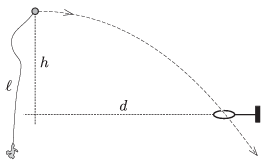
Data: \(\displaystyle \ell=1.6\) m, \(\displaystyle h=1.25\) m, \(\displaystyle d=2\) m.
(5 pont)
P. 4699. Two thin sheets on the surface of a slope of angle of elevation of \(\displaystyle \alpha=30^\circ\) form a pair of rails. The distance between the sheets is \(\displaystyle d=1.6\) cm. A ball of diameter of 2 cm is placed to the rails and it rolls down without slipping.
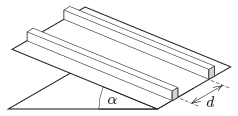
\(\displaystyle a)\) Calculate the acceleration of the centre of the ball.
\(\displaystyle b)\) If the coefficient of friction is \(\displaystyle \mu\), at what angle of elevation will the ball slip on the rails?
(5 pont)
P. 4700. A uniform metal disc of height \(\displaystyle h\) and of cross section \(\displaystyle A\) (\(\displaystyle h\ll \sqrt{A}\)) is moving at a great acceleration parallel to the symmetry axis of the disc (\(\displaystyle {a\gg g}\)). How many electrons appear at that side of the disc which is opposite of the direction of the acceleration?
(5 pont)
P. 4701. Small balls of charge \(\displaystyle Q\) are attached to the points \(\displaystyle P_1\) and \(\displaystyle P_2\) of a ring, made of some insulating material, moving in a vertical plane, such that \(\displaystyle \alpha=60^\circ\). The ring is in a homogeneous magnetic field of induction \(\displaystyle B\), the magnetic field lines are perpendicular to the plane of the ring. The ring is moved such that it rolls without skidding on the horizontal surface which is also made from some insulating material. The speed of the centre of the ring is \(\displaystyle v_0\).
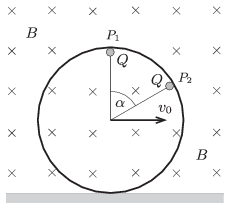
\(\displaystyle a)\) What is the magnitude of the magnetic force exerted on each charge at the position shown in the figure?
\(\displaystyle b)\) At which positions of the ring will the torque of the sum of the magnetic forces calculated about the centre of the ring be zero? Considering only these positions, in which case will the force exerted by the magnetic field on the ring be the greatest and what is this greatest force?
\(\displaystyle c)\) Determine the intersection of the lines of action of the magnetic forces.
(5 pont)
P. 4702. Four concrete cubes, which are made of different material, and which all have the side of 10 cm are placed next to each other as shown in the figure. They are ``illuminated'' by a beam of \(\displaystyle {}^{60}\)Co gamma-ray, from four different positions, (S1, S2, S3 and S4) one after the other. Opposite to the gamma source behind the cubes there are four detectors (D1, D2, D3 and D4). The first three measurements shows that the concrete cubes decrease the intensity of the radiation by 86.76, 71.94 and 84.25 percent of the original value, respectively.
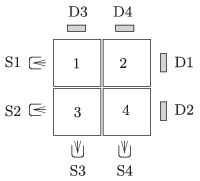
\(\displaystyle a)\) What is the intensity of the radiation measured by the fourth detector, expressed in the percentage value of the intensity of the original radiation?
\(\displaystyle b)\) The ``thickness of the halving-layer'' of the first cube is 6 cm. What is this value for the other cubes (which is characteristic of the material of the cube)?
(5 pont)
P. 4703. The resistance of each pieces of wire between the points indicated by the black circles in the arrangement (the pattern continues infinitely towards the centre) shown in the figure is \(\displaystyle 1~\Omega\).
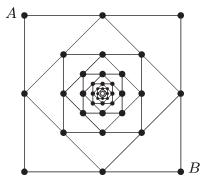
What is the equivalent resistance between the points \(\displaystyle A\) and \(\displaystyle B\)?
(6 pont)
Upload your solutions above.
