KöMaL Problems in Mathematics, January 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 10, 2015. |
K. 445. Corner \(\displaystyle P\) of a square \(\displaystyle PQRS\) is folded up to coincide with corner \(\displaystyle R\). Then \(\displaystyle Q\) is also folded to \(\displaystyle R\). The area of the resulting figure is 9 cm\(\displaystyle {}^{2}\). What is the area of the original square?
(6 pont)
K. 446. John works for two companies, each paying him by the hour. If he works twice as much for the first company than for the second one during the course of a month, then his monthly wages will be 4/5 as much as they would be if he did it the other way round. How long does he need to work for the first company to earn as much as he is paid by the second company for 10 hours?
(6 pont)
K. 447. Are there natural numbers \(\displaystyle x\) and \(\displaystyle y\) such that \(\displaystyle x^{2}+y^{2}=2015\)?
(6 pont)
K. 448. There are four discs on a carousel, arranged as shown in the diagram. In how many ways is it possible to colour the four discs with four colours, given that colourings obtained from each other by rotating the carousel around its midpoint in its plane are not considered different? Any colour may be chosen for any disk, but each disc is only allowed to have a single colour.
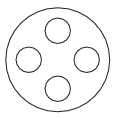
(6 pont)
K. 449. Sebastian's test score of 98 points increased his average calculated from all previous tests by 1 point. Then his next score of 70 points decreased the average by 2 points. How many tests did Sebastian take altogether?
(6 pont)
K. 450. In the arithmetic sequence \(\displaystyle 1, 14, 27, \ldots,\) how many digits are there in the second number that consists of digits of 2 only?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 10, 2015. |
C. 1266. Solve the equation \(\displaystyle 5(2n+1)(2n+3)(2n+5) =\overline{ababab}\), where \(\displaystyle n\) denotes a positive integer, \(\displaystyle a\) and \(\displaystyle b\) stand for different digits, and \(\displaystyle \overline{ababab}\) is a six-digit number.
Suggested by L. Számadó, Budapest
(5 pont)
C. 1267. Given a convex angle in the plane and a point \(\displaystyle S\) in its interior, determine the line (e.g. by providing a method of construction) that forms a triangle with the vertex of the given angle such that the centroid of the triangle is the given point.
(5 pont)
C. 1268. Prove that for all real numbers \(\displaystyle a\) and \(\displaystyle b\), \(\displaystyle a^4+b^4+2\ge 4ab\).
(5 pont)
C. 1269. What is the minimum number of sides of a regular polygon in which the radius of the circumscribed circle is at most 1.1 times the radius of the inscribed circle?
(5 pont)
C. 1270. There are a few lines and a few circles drawn on a sheet of paper. Every two of them intersect each other, but no three pass through the same point. What are the numbers of lines and of circles if the number of intersection points is 75?
(5 pont)
C. 1271. Consider circumscribed circle of a right-angled triangle. Draw the semicircle containing the triangle, and draw tangents to it, parallel to the legs. The parallels together with the line of the hypotenuse form a similar right-angled triangle.
Find the angles of the triangle if the area of the outer triangle is 6 times the area of the inner triangle.
Based on the idea of I. Légrádi, Sopron
(5 pont)
C. 1272. The sum of an arithmetic progression of 100 terms is 838 without the 68th term, and 849 without the 13th term. What are the values of the terms left out?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 10, 2015. |
B. 4678. Ann and Bill take turns writing digits on a sheet of paper, left to right. Ann starts with a nonzero digit, and they continue until a 100-digit number is formed. Bill wins if the resulting number divided by 11 leaves a remainder of 5, otherwise Ann wins. Both players are good at mathematics. Who will win the game?
Suggested by Gy. Károlyi, Budajenő
(4 pont)
B. 4679. Prove that among any 39 consecutive natural numbers there is a number in which the sum of the digits is divisible by 11.
(3 pont)
B. 4680. Find the integer solutions of the equation \(\displaystyle 3^{n}=2n^2+1\)
(3 pont)
B. 4681. What is the area of the pentagon in exercise C. 1240.?
(4 pont)
B. 4682. For a given positive integer \(\displaystyle k\), find the largest positive integer \(\displaystyle m\) such that the following statement should be true: If at most \(\displaystyle m\) of \(\displaystyle 3k\) different points in the plane are collinear, then the points can be divided into \(\displaystyle k\) groups of three such that the points in each group form a triangle.
Suggested by A. Frank, Nagykovácsi
(5 pont)
B. 4683. Is there a plane that intersects a right pyramid of regular pentagonal base in a hexagon with
\(\displaystyle a)\) line symmetry,
\(\displaystyle b)\) central symmetry?
(6 pont)
B. 4684. The diagonals of a quadrilateral \(\displaystyle ABCD\) are perpendicular, they intersect at \(\displaystyle E\). From point \(\displaystyle E\), drop a perpendicular onto the line of each side. Consider the intersection of each perpendicular with the opposite side. Prove that the four points all lie on a circle centred at a point of the line segment connecting the midpoints of the diagonals.
Suggested by Sz. Miklós, Herceghalom
(5 pont)
B. 4685. Determine the smallest possible value of \(\displaystyle x^{2}+y^{2}+z^{4}\), where \(\displaystyle x\), \(\displaystyle y\) and \(\displaystyle z\) are positive numbers that add up to 34.
(5 pont)
B. 4686. A flea is jumping on the points of the plane with integer coordinates. Is it possible for the flea to follow a route touching every lattice point exactly once, in which each jump has an integer length, and each integer jump length occurs exactly once?
(6 pont)
 |
Problems with sign 'A'Deadline expired on February 10, 2015. |
A. 632. Let \(\displaystyle ABCD\) be a convex quadrilateral. In the triangle \(\displaystyle ABC\) let \(\displaystyle I\) and \(\displaystyle J\) be the incenter and the excenter opposite to vertex \(\displaystyle A\), respectively. In the triangle \(\displaystyle ACD\) let \(\displaystyle K\) and \(\displaystyle L\) be the incenter and the excenter opposite to vertex \(\displaystyle A\), respectively. Show that the lines \(\displaystyle IL\) and \(\displaystyle JK\), and the bisector of the angle \(\displaystyle BCD\) are concurrent.
Russian problem
(5 pont)
A. 633. Prove that if \(\displaystyle n\) is a sufficiently large positive integer then among any \(\displaystyle n\) distinct positive integers there are four whose least common multiple is greater than \(\displaystyle n^{3.99}\).
(5 pont)
A. 634. Let \(\displaystyle n\ge2\) be a in integer and let \(\displaystyle f\colon \mathbb{R}\to[-1,1]\) be an \(\displaystyle n\) times differentiable function. Show that the equation \(\displaystyle f^{(n)}(x)=0\) has at least \(\displaystyle n-1\) distinct solutions.
(5 pont)
Upload your solutions above.
