KöMaL Problems in Mathematics, February 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 10, 2015. |
K. 451. In the game of rock-paper-scissors, players need to observe three rules: the rock blunts the scissors, the scissors cut the paper, and the paper wraps the rock. These rules decide which weapon wins. How many new rules need to be formulated if four extra weapons are added to the game (for example, matchstick, spectacles, telephone, stamper)? What is the fundamental principle of forming the rules, in order that the new game should be balanced, like the original game?
(6 pont)
K. 452. A silo for storing winter food for cattle is attached to one corner of a rectangular stable. The silo is shaped like a regular triangular prism, with base edges of length 3 metres. The longer side of the stable is 9 metres. With a 9-metre-long rope, a goat is tied to the point where the silo joins with the stable (see the figure). The goat cannot break the rope, and the rope will not stretch. The buildings are surrounded with grass, and there is no fence or any other obstacle hindering the goat from grazing. Find the area that the goat can graze.
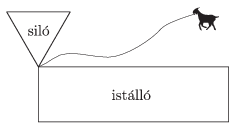
(6 pont)
K. 453. The mean mark on a test was 71 points. However, the teacher made a mistake in assessing one of the problems, so every student was given an extra point. Thus the total mark on the papers changed to 936. How many students took the test?
(6 pont)
K. 454. Several digits of the numbers in the operations below have been replaced with letters. Different letters stand for different digits, and identical letters stand for identical digits. No letter denotes the digit 1.
\(\displaystyle 1 \cdot \mathrm{G} + 1 = \mathrm{H}, \)
\(\displaystyle 1\mathrm{A} \cdot \mathrm{G} + 2 = \mathrm{HG}, \)
\(\displaystyle 1\mathrm{AB} \cdot \mathrm{G} + 3 = \mathrm{HGF}, \)
\(\displaystyle 1\mathrm{ABC} \cdot \mathrm{G} + 4 = \mathrm{HGFE}, \)
\(\displaystyle 1\mathrm{ABCD} \cdot \mathrm{G} + 5 = \mathrm{HGFED}.\)
Find the value of each letter.
(6 pont)
K. 455. The representation of 2015 in binary notation is a palindrome number: 11111011111. How many years are there in the 21st century whose binary representations are also palindromes?
Based on the idea of S. Kiss, Nyíregyháza
(6 pont)
K. 456. The representations of three consecutive square numbers in base \(\displaystyle b\) notation are 220, 251 and 304. Find the value of \(\displaystyle b\).
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 10, 2015. |
C. 1273. Prove that \(\displaystyle 3^{4n}+4\cdot 7^{4k}\) is divisible by 5 for all \(\displaystyle n,k\in \mathbb{N}\).
(5 pont)
C. 1274. The 482 employees of a company are taking a team building trip. They can use vehicles seating 4, 19 or 21 people. How many of each kind of vehicle should be used, provided that each vehicle needs to be full? Find all possible solutions.
(5 pont)
C. 1275. Determine the largest five-digit positive integer \(\displaystyle \overline{abcde}\) that is divisible by each of the numbers \(\displaystyle \overline{bcde}\), \(\displaystyle \overline{cde}\), \(\displaystyle \overline{de}\) and \(\displaystyle e\).
(5 pont)
C. 1276. \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle Z\), \(\displaystyle V\) are interior points of sides \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DA\) of a parallelogram \(\displaystyle ABCD\), respectively, such that \(\displaystyle \frac{AX}{XB} =\frac{BY}{YC} =\frac{CZ}{ZD} =\frac{DV}{VA}=k\), where \(\displaystyle k\) is a positive constant less than \(\displaystyle \frac 12\). Find the value of \(\displaystyle k\), given that the area of quadrilateral \(\displaystyle XYZV\) is 68% of the area of parallelogram \(\displaystyle ABCD\).
(5 pont)
C. 1277. Depending on the value of \(\displaystyle r^2\), how many solutions do the simultaneous equations \(\displaystyle x^2 + y^2 =r^2\), \(\displaystyle |x| + |y| =2\) have?
(5 pont)
C. 1278. Determine the value of \(\displaystyle n\), given that \(\displaystyle \binom n1\), \(\displaystyle \binom n2\) and \(\displaystyle \binom n3\) are three consecutive terms of an increasing arithmetic progression.
(5 pont)
C. 1279. Determine all squares that have vertex \(\displaystyle A\) at the point \(\displaystyle (4;-2)\), vertex \(\displaystyle B\) on the circle \(\displaystyle b\colon {(x-5)}^2+ {(y-2)}^2=25\), and vertex \(\displaystyle D\) on the line \(\displaystyle d\colon 4x+3y+2=0\).
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 10, 2015. |
B. 4687. Samson wrote the number 123456789 on a sheet of paper. Then he may or may not have placed a multiplication sign between any two consecutive digits. (He may have used several of them, or none at all.) By reading the digits between multiplication signs as a single number, he obtained a product of numbers. For example, \(\displaystyle 1234 \cdot 56 \cdot 789\). What is the maximum possible value of the number obtained in this way?
Suggested by M. E. Gáspár, Budapest
(3 pont)
B. 4688. Which of the numbers below is greater if each expression contains 50 twos and 50 threes alternating: \(\displaystyle 2^{3^{\scriptstyle 2^{\scriptstyle 3^{\scriptstyle .^{\scriptstyle .^{\scriptstyle .^{\scriptstyle 2^{\scriptstyle 3}}}}}}}}\) or \(\displaystyle 3^{2^{\scriptstyle 3^{\scriptstyle 2^{\scriptstyle .^{\scriptstyle .^{\scriptstyle .^{\scriptstyle 3^{\scriptstyle 2}}}}}}}}\)?
(5 pont)
B. 4689. Is there a pentagonal pyramid that can be intersected by a plane in a regular hexagon?
(6 pont)
B. 4690. 9 mathematicians of a university went to a conference together. Since the presentations were boring, they fell asleep several times, each of them at most 4 times. For any pair of mathematicians, there was a time when they were both sleeping. Show that there was a time instant when at least three of them were sleeping.
(5 pont)
B. 4691. \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) and \(\displaystyle d\) are four parallel lines in the plane, in this order. The distance of \(\displaystyle a\) and \(\displaystyle b\) is 1, the distance of \(\displaystyle b\) and \(\displaystyle c\) is 3, and the distance of \(\displaystyle c\) and \(\displaystyle d\) is also 1. Consider the rectangles that have exactly one vertex on each line. How can we obtain the rectangle of minimal area, and what is this area?
(3 pont)
B. 4692. The sides of an acute-angled triangle are \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), the opposite angles are \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\), and the lengths of the corresponding altitudes are \(\displaystyle m_a\), \(\displaystyle m_b\), \(\displaystyle m_c\), respectively. Prove that \(\displaystyle \frac{m_a}{a} + \frac{m_b}{b} + \frac{m_c}{c} \ge 2\cos \alpha \cos\beta \cos \gamma \left(\frac{1}{\sin 2\alpha} + \frac{1}{\sin 2\beta} + \frac{1}{\sin 2\gamma}\right) + \sqrt{3}\,\).
Suggested by K. Williams, Szeged
(5 pont)
B. 4693. \(\displaystyle K\) is a point on side \(\displaystyle AC\) of triangle \(\displaystyle ABC\) such that \(\displaystyle AK=2KC\) and \(\displaystyle \angle ABK = 2 \angle KBC\). Let \(\displaystyle F\) denote the midpoint of side \(\displaystyle AC\), and let \(\displaystyle L\) be the orthogonal projection of point \(\displaystyle A\) onto the line segment \(\displaystyle BK\). Prove that the lines \(\displaystyle FL\) and \(\displaystyle BC\) are perpendicular.
(5 pont)
B. 4694. Find all real numbers \(\displaystyle p_1\), \(\displaystyle q_1\), \(\displaystyle p_2\), \(\displaystyle q_2\) such that \(\displaystyle p_2\) and \(\displaystyle q_2\) are roots of the equation \(\displaystyle x^3+p_1x+q_1=0\), and \(\displaystyle p_1\) and \(\displaystyle q_1\) are roots of the equation \(\displaystyle x^3+p_2x+q_2=0\).
Suggested by Z. Bertalan, Békéscsaba
(4 pont)
B. 4695. Given that a permutation of the points of the plane maps any three concyclic points to three concyclic points, show that three points are collinear if and only if their images are collinear.
(5 pont)
 |
Problems with sign 'A'Deadline expired on March 10, 2015. |
A. 635. Show that for every positive real number \(\displaystyle c>0\) there is a positive integer \(\displaystyle n\) such that \(\displaystyle \varphi\big(\sigma(n)\big)>cn\). (For an arbitrary postive integer \(\displaystyle k\), \(\displaystyle \varphi(k)\) denotes the number of positive integers not exceeding \(\displaystyle k\) that are co-prime with \(\displaystyle k\). \(\displaystyle \sigma(k)\) is the sum of positive divisors of \(\displaystyle k\).)
Proposed by: Barnabás Szabó, Budapest
(5 pont)
A. 636. There is given a convex quadrilateral \(\displaystyle ABCD\) and a point \(\displaystyle P\) in the interior of the triangle \(\displaystyle BCD\) in such a way that the quadrilateral \(\displaystyle ABPD\) has an inscribed circle, and the three inscribed circles of the quadrilateral \(\displaystyle ABPD\), the triangle \(\displaystyle BCP\) and the triangle \(\displaystyle CDP\), respectively, are pairwise tangent to each other. Denote by \(\displaystyle Q\) and \(\displaystyle R\) the points tangency on the line segments \(\displaystyle BP\) and \(\displaystyle DP\), respectively. Let the lines \(\displaystyle BP\) and \(\displaystyle AR\) meet at \(\displaystyle S\), let the lines \(\displaystyle DP\) and \(\displaystyle AQ\) meet at \(\displaystyle T\), and let the lines \(\displaystyle BT\) and \(\displaystyle DS\) meet at \(\displaystyle U\). Show that the line \(\displaystyle CU\) bisects the angle \(\displaystyle BCD\).
(5 pont)
A. 637. Let \(\displaystyle n\) be a positive integer. Let \(\displaystyle \mathcal{F}\) be a family of sets that contains more than half of all subsets of an \(\displaystyle n\)-element set \(\displaystyle X\). Prove that from \(\displaystyle \mathcal{F}\) we can select \(\displaystyle \lceil\log_2n\rceil+1\) sets that form a separating family on \(\displaystyle X\), i.e., for any two distinct elements of \(\displaystyle X\) there is a selected set containing exactly one of the two elements.
Miklós Schweitzer competition, 2014
(5 pont)
Upload your solutions above.
