KöMaL Problems in Informatics, March 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on April 10, 2015. |
I. 370. There is only one old and unstable suspension bridge over a wild mountain river. The bridge consists of cables attached together, and of some planks lying across the cables. At some places there are gaps between the planks, so we want to repair the bridge or rearrange the planks, but we have only a few extra of them.
Someone measured the gaps between the planks from the left bank to the right bank of the river. The file hid.txt, downloadable from our webpage, contains these data in centimeters.
The first line of the file contains the length \(\displaystyle H\) of the suspension bridge (\(\displaystyle 300\le H\le 50\;000\)). The second line contains the theoretically determined safe step length \(\displaystyle L\) (\(\displaystyle 40\le L\le 80\)). The following \(\displaystyle N\) lines (\(\displaystyle 1\le N\le H\)) contain the distance between the planks. Walking through the planks is safe, if any plank distance is smaller then the step length \(\displaystyle L\) (since each plank is narrow, its width is neglected).
For example (with / denoting a newline character): 352 / 75 / 28 / 74 / 84 / 22 / 69 / 73 / ...
In the example, the bridge length is 352 cm, the safe step length is 75 cm, the distance between the first plank and the left bank of the river is 28 cm, the distance between the first plank and the second plank is 74 cm, and so on.
Your program i370 should solve the following tasks.
Before writing any result to the screen, the number of the actual task (for example, Task 4) should be displayed. Diacritical marks in the output may be omitted.
1. Read the data from the file hid.txt and solve the following tasks.
2. Display the distance between the last plank and the right bank of the river.
3. Determine the distance (in cm) up to which we can walk safely on the bridge starting from the left bank. If the entire bridge is safe, then you should display this information.
4. Display the longest connected bridge segment where walking through is not safe, by specifying the starting and final plank numbers of this segment.
5. We want to remove a single plank. In how many ways can we do this such that one can still walk safely through the newly introduced gap?
6. Collect and display all neighboring plank pairs between which at least one new plank should be installed to make the bridge safe. For example: 2-3.
7. Give the minimum number of planks to be installed to make the bridge safe.
8. Two people would like to cross the original old bridge by holding each other's hands. They agree that no two feet will be put on the same plank. Moreover, they carry some extra planks to put down temporarily in front of them when necessary; after they pass over that plank, the second person can get it again within 1 step length and give it back to the first person. Determine the minimum number of planks they have to carry so that they can safely cross the bridge. Planks originally attached to the bridge cannot be removed.
Example: the feet positions of person A and person B as they move along:
A_foot1 5, A_foot2 4, B_foot1 3, B_foot2 2, B can get the first plank if it is not attached and give it to A. A can put down a plank in front of them at distance \(\displaystyle L\), A_foot2 6, B_foot2 4, he can get the second plank ...
The source code (i370.pas, i370.cpp, ...) of your program with its short documentation (i370.txt, i370.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted.
Downloadable file: hid.txt
(10 pont)
I. 371. Duties of technical managers of sports clubs include coordinating the schedule of different team matches in a tournament. The source file merkozesek.txt contains an up-to-date monthly calendar with a schedule of the team matches. Unlike us, the technical manager does not have much experience with spreadsheet applications: he can register in the table that a team will have a match on a particular date, or, if the match is canceled, he can delete the team name, but he cannot perform other editing tasks. The sports association has 8 teams, and there can be at most 15 days in each month when teams can play.
In the example, ``fiú'' is boy, ``lány'' is girl, ``serdülő'' is teenager, ``férfi'' is man, ``nő'' is woman, and ``felnőtt'' is adult.
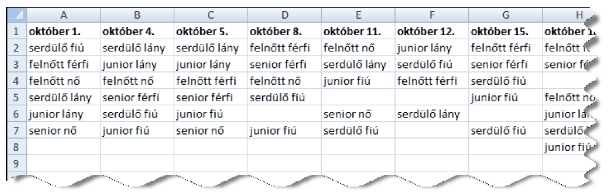
You should help the technical manager creating and handling the team data by using a spreadsheet application and solving the following tasks. User-defined functions and macros cannot be used in your solution.
1. Open the tabulator-separated and UTF-8 encoded text file merkozesek.txt (= matches) in the spreadsheet application according to the example. Your solution should work properly even if the data are changed. Save your work as i371 in the default application file format.
2. Create a new sheet that will display data and the corresponding information for one team.
The example shows a sheet for the teenager boy team. ``Mérkőzések időpontja'' is the date of the matches, ``Mérkőzések száma'' is the number of matches, ``Legkisebb pihenő'' is the minimum number of days (= nap) with rest, and ``Egymás utáni napok'' is consecutive days.
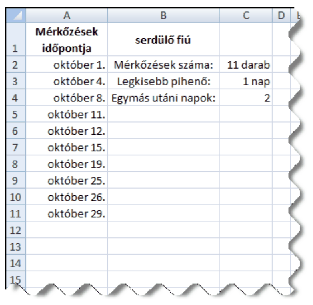
3. According to the example, create the sheet structure, then make the headers for the first line and the labels for column B. You can perform auxiliary computations to the right of column D. These computations should have some remarks or labels so that it is easier to understand them.
4. Cell B2 should contain the team name the actual sheet refers to. If we copy the sheet and change the team name, the corresponding team information should appear.
5. Cells A2 and below should contain the dates when the current team has a match. The dates should be sorted, with no empty cells between them. Your sheet should work for the possible 15 days. Cells below the last match should remain empty.
6. Cell C2 should contain the number of matches in the actual month.
7. Cell C3 should contain the minimum number of days with rest between two consecutive matches.
8. Cell C4 should contain how many times the team will have matches on consecutive days in the actual month.
9. The sheet should be formatted, and column C should contain the units according to the example.
10. Create at least two copies of the sheet. Modify their cell B2 to display the corresponding information for two other teams. The sheet name should be changed to be the same as the team name.
The spreadsheet (i371.xls, i371.ods, ...) together with a short documentation (i371.txt, i371.pdf, ...), also containing the name and version number of the spreadsheet application should be submitted.
The downloadable file necessary to solve the task: merkozesek.txt
(10 pont)
I. 372. OpenGL is a platform-independent programming interface to display 3D objects. Many C programs are written for it, but other programming languages appearing in the contest rules of this journal, e.g., Lazarus or Visual Basic, are also used. Several references, videos and sample programs can be found on the Internet to learn its programming. It is worth using GLUT or other OpenGL toolkits available in the given programming language or environment.
Create an OpenGL application to simulate the path of a point-like object bouncing slowly within a cube. Your program should display the edges of the cube, and trace the object trajectory. The object should have a random initial velocity, and all collisions with the walls should be perfectly elastic. You should use perspective projection to display the 3D objects. The user should be able to zoom in or out, and there should be an option in which the ``camera'' is always directed toward the cube center.
You should submit in a compressed file i372.zip the documentation of your program (i372.txt, i372.pdf) and the necessary source files for compiling the program. The documentation should explicitly specify which programming language and environment, and which toolkits should be used to compile and run your program.
(10 pont)
 |
Problems with sign 'S'Deadline expired on April 10, 2015. |
S. 97. Elephants in a herd are walking calmly in a single line. Elephants are numbered from 1 to \(\displaystyle N\) (\(\displaystyle 1\le N\le 100\;000\)). Elephant 1 is the smallest one, then gradually, Elephant \(\displaystyle N\) is the largest animal of them. It would be nice to have the smallest elephant in the first place, then the second smallest, and so on. However, currently they are not necessarily in this order. We say that a pair of elephants from the line is in wrong order, if the larger animal precedes the smaller. You should determine the number of pairs in wrong order.
Your program should read the value of \(\displaystyle N\) from the first line of the standard input, then \(\displaystyle N\) numbers from the next line denoting the elephants in the line. The first and only line of the standard output should contain the number of elephant pairs in wrong order.
In the example, ``Példa bemenet'' is sample input, while ``Példa kimenet'' is the corresponding output.
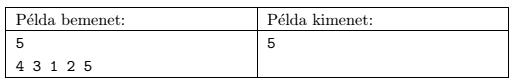
Explanation: the pairs (1,3), (1,4), (2,3), (2,4) and (3,4) are in wrong order.
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time.
The source code (s97.pas, s97.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s97.txt, s97.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s97.zip.
(10 pont)
$Var(Body)
Upload your solutions above
