KöMaL Problems in Physics, April 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 11, 2015. |
M. 350. Determine the pressure of the gas in the bulb of a traditional gas filled filament lamp.
(6 pont)
 |
Problems with sign 'P'Deadline expired on May 11, 2015. |
P. 4725. The diameter of a standard table-tennis ball is 40 mm, and its mass is 2.7 grams. What is the diameter of that iron ball, which should be attached to the table-tennis ball, in order that they just float in the water?
(3 pont)
P. 4726. A narrow circular sector of a black disc is painted white. The disc is rotated about an axis which goes through its centre, and is perpendicular to the disc, and the rotated disc is illuminated with strobe light (a periodically flashing light source). What is the relationship between the number of revolutions \(\displaystyle n\) of the disc and the flashing frequency \(\displaystyle f\), if not only one, but a number of \(\displaystyle p\) seemingly steady white sectors can be observed on the disc (\(\displaystyle p=2, 3, 4, \ldots\))?
(4 pont)
P. 4727. Different shapes of planar figures, which have the same area, are cut from a uniform metal sheet. What is the shape of that figure which has the least moment of inertia calculated around an axis which goes through the centre of mass of the figure and which is perpendicular to the plane of the figure?
(4 pont)
P. 4728. Philae, the lander of the space probe called Rosetta, landed on the nucleus of a comet of mass \(\displaystyle 10^{13}\) kg, and of average density 0.4 g/cm\(\displaystyle {}^3\), which is due to the fact that inside the nucleus there are voids. The landing was ``bouncy'', Philae arrived back to the surface of the nucleus of the comet 113 minutes later after its first bounce. Give estimation for the following:
\(\displaystyle a)\) What is the gravitational field strength on the surface of the nucleus of the comet, and what is the escape speed?
\(\displaystyle b)\) What was the least speed of the first bounce, and to what greatest height could Philae bounce back?
For the estimation, the nucleus of the comet can be considered as a uniform sphere, which is not rotating, and the motion can be considered as uniformly accelerated. For determining the average acceleration use the exact relationship between the speed and the height of the bouncing.
(5 pont)
P. 4729. An easily moveable piston of mass \(\displaystyle M=80\) kg is suspended by a thread in a vertical cylinder of inner cross section \(\displaystyle A=5~{\rm dm}^2\), and encloses a sample of air at a temperature of \(\displaystyle T_0=300\) K. The piston is attached to the ceiling by an unstretched spring of spring constant \(\displaystyle D=6\) N/cm. The length of the air column is \(\displaystyle \ell_0=1.2\) m, and initially the pressure inside and outside is \(\displaystyle p_0=10^5\) Pa. At a moment the thread breaks.
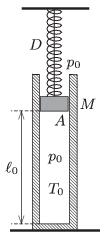
\(\displaystyle a)\) What will the greatest speed of the piston be during the initiated process?
\(\displaystyle b)\) During the process what will the greatest temperature of the enclosed sample of air be?
(5 pont)
P. 4730. The terminal voltages across the voltage supplies connected as shown in the figure are constant. The voltage across the capacitor \(\displaystyle C\) is \(\displaystyle 1.8\,U_0\). If the terminals of the voltage supply \(\displaystyle U_0\) is swapped over then the voltage across the capacitor decreases to \(\displaystyle 1.4\,U_0\). Determine the ratios of \(\displaystyle r/R\) and of \(\displaystyle u_0/U_0\).
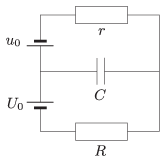
(4 pont)
P. 4731. Which is greater: the energy of one photon emitted by a filament lamp made of Tungsten and filled with Krypton, or the average kinetic energy of an atom of the Krypton gas in the lamp, when the lamp is operated?
(4 pont)
P. 4732. In a cyclotron protons, deuterons and \(\displaystyle \alpha\)-particles are accelerated. The radius of the greatest circular path is 50 cm. The magnitude of magnetic flux density is 1 Tesla. To what greatest energy can these particles be accelerated in this cyclotron?
(4 pont)
P. 4733. Light-rays travel in a cylinder shaped glass rod parallel to the symmetry axis of the rod, and when they enter to air at the end of the rod they brought to focus at one point. Give the equation of the boundary curve in terms of the refractive index of glass \(\displaystyle n\), and of the focal length \(\displaystyle f\).
(4 pont)
P. 4734. Three small positively charged balls of mass \(\displaystyle m\) are attached by massless insulating threads of length \(\displaystyle L\) and are placed to a horizontal smooth surface made of some insulating material. Two of the balls both have a charge of \(\displaystyle Q\) and the third is charged to \(\displaystyle 2Q\). At an instant the thread between the two balls of charge \(\displaystyle Q\) is cut off.
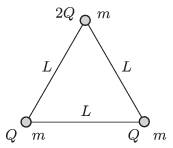
\(\displaystyle a)\) What are the velocities of the balls at the instant when the ball of charge \(\displaystyle 2Q\) is the fastest?
\(\displaystyle b)\) What is the tension in the threads at this moment?
\(\displaystyle c)\) What are the displacements of the balls at this moment?
(5 pont)
P. 4735. The Examining Institute for Cosmic Accidents (EXINCA) sent the following short report to one of its experts: ``One of the discovery spaceships of the Titanium-Devouring Little Green Men has found a perfectly spherical uniform Titanium asteroid. In order to make preparations for the mining, a straight tunnel was built and rails were put into it. The length of the tunnel was the same as the radius of the asteroid, and both ends of the tunnel were on the surface of the planet. Unfortunately one of the mine-carts, although its brake was applied, slipped into the shaft at one end of the tunnel. Initially it speeded up, then it slowed down gradually, turned back and then it stopped exactly at the middle of the tunnel. When it turned back it nearly hit the leader of the miners.'' EXINCA asked the expert to calculate the following:
\(\displaystyle a)\) Where (at what fraction of the length of the tunnel) did the leader of the miners stand?
\(\displaystyle b)\) What could the coefficient of kinetic friction between the wheels of the mine-cart and the rails be?
\(\displaystyle c)\) How long did the mine-cart move if the period of the spacecraft revolving next to the surface of the asteroid is 24 hours? (The asteroid has no atmosphere.)
(6 pont)
Upload your solutions above.
