A KöMaL 2015. szeptemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
I. 379. A nyugatot benépesítő telepesek sokan ismerték egymást, akár még leveleztek is volna, de arról gyakran fogalmuk sem volt, hogy egy másik család vajon merre lehet. Postakocsi nem volt, csak a szomszédok találkoztak. Mivel más módjuk nem volt, a terület feltérképezésére a következőt találták ki:
Ha két szomszéd találkozik, akkor kicserélik ismereteiket. Ez azt jelenti, hogy egyik a másiktól megtudja, hogy az kikről tud már. Ha az adott illetőről még nem tudott, akkor feljegyzi a nevét és azt, hogy kitől hallott róla. Ha ezután bármilyen üzenetet kíván egyik telepes egy másiknak eljuttatni, akkor azt kéri meg a továbbításra, akitől először hallott róla.
Megfelelően sok találkozás után mindenki tudomást szerez a terület minden telepeséről.
Feltételezzük, hogy kezdetben mindenki ismeri a szomszédjait, de más családokat nem. A szomszed.txt fájl tartalmazza a szomszédság leírását. A talalkozas.txt pedig a találkozásokat írja le időrendben (ki, kivel).
A standard bemenetről olvassuk be, hogy ki kinek akar üzenetet küldeni. Határozzuk meg, hogy hányadik találkozást követően indíthatja útjára az üzenetet, valamint azt, hogy az üzenet milyen úton jut el a címzetthez.
Példa (a többsoros bemeneteknél a példában a sortörések helyett / jelet írtunk):
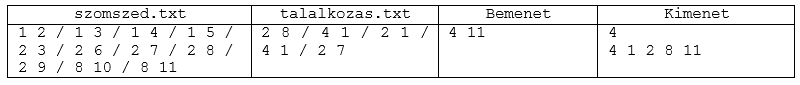
A lap nyomtatott változatában a példa hibás volt, ez egy helyes példa.
Beküldendő egy tömörített i379.zip állományban a program forráskódja és megoldás rövid leírását bemutató dokumentáció, amely egyben megadja, hogy a forrás mely fejlesztő környezetben fordítható.
(10 pont)
I. 380. Táblázatkezelő programokkal viszonylag könnyű meghatározni, hogy egy adott dátum milyen napra esik. Sajnos ezek a programok az 1900. január 1. előtti dátumokat nem kezelik. Ezekben az esetekben a ,,számítógép előtti idők'' hagyományos módszerét alkalmazhatjuk, amely három segédtáblából áll. Az első segédtábla az évhez rendel egy indexszámot, a második az így kapott indexszámhoz és a hónap sorszámához ad egy kulcsszámot. Végül az így kapott kulcsszám és a nap sorszámának összegéből a harmadik tábla adja meg a nap nevét.
Példánkban 1848. március 15-ét keressük. Az 1848-hoz tartozó indexszám 45, a 45-höz és a márciushoz tartozó kulcsszám pedig 2. Végül \(\displaystyle 2+15\) összegét visszakeresve szerdát kapunk.
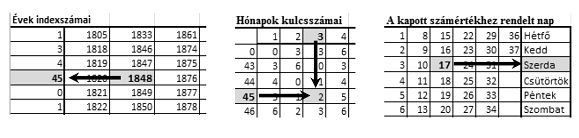
Ebben a feladatban a segédtáblák birtokában kell elkészítenünk egy táblázatkezelő munkalapját úgy, hogy az meghatározza, milyen napra esett egy adott dátum. A segédtáblákat a tablak.txt UTF kódolású, tabulátorokkal tagolt állomány tartalmazza.
1. Töltsük be a táblázatkezelő program egyik munkalapjára az A1 cellától kezdve a tablak.txt adatfájlt, majd mentsük a munkafüzetet oroknaptar néven a program alapértelmezett formátumában.
2. Első feladatunk az év indexszámának meghatározása, amit két lépésben fogunk elvégezni. Első lépésben képlet segítségével jelenítsük meg a 36. sor celláiban, hogy a C2 cellában megadott év a B5:T35 segédtábla adott oszlopában hányadik sorban szerepel. Ha az adott oszlopban nem szerepel az évszám, úgy a 36. sor megfelelő cellájában 0-t jelenítsünk meg.
3. Második lépésben függvény segítségével jelenítsük meg a C1 cellában lévő év indexszámát a C2 cellában. Az indexszámot az A5:A35 tartományban találjuk, sorszámát a 36. sor 0-tól különböző eleme adja meg.
4. Következő feladatunk a kulcsszám meghatározása az E2 cellában. A kulcsszám az előzőekben meghatározott indexszámtól és a hónap E1 cellában megadott sorszámától függ. A kulcsszámot az A39:M53 segédtáblából kell függvény alkalmazásával visszakeresnünk, a segédtábla oszlopait a hónapok azonosítják (B39:M39), sorait pedig az indexszámok (A40:A53).
5. A nap visszakereséséhez határozzuk meg képlettel a G2 cellában a kapott kulcsszám (E2) és a nap sorszámának (G1) összegét.
6. Utolsó lépésként meghatározzuk az adott nap elnevezését. Ehhez keressük meg képlet alkalmazásával az A57:G63 segédtáblában a G2 cellában kapott összeget, és írassuk az I2 cellába a szám sorában, az utolsó oszlopban található nap nevét.
7. Mindhárom segédtábla (A5:T35, A39:M53, A57:G63) celláit határoljuk belül vékony, kívül vastag vonallal. A megadott dátumhoz tartozó három cella, valamint a nap elnevezését tartalmazó cella tartalma legyen félkövér, háttere pedig halványszürke.
8. Feltételes formázás alkalmazásával emeljük ki félkövér, sötétvörös színnel:
\(\displaystyle a)\) a B5:T39 segédtáblából a C1 cellában szereplő évszámot,
\(\displaystyle b)\) a B39:M39 oszlopfejlécből az E2 cellában szereplő hónapot,
\(\displaystyle c)\) az A40:A53 sorfejlécből az C2 cellában szereplő indexszámot, és
\(\displaystyle d)\) a A57:F63 segédtáblából a G2 cellában szereplő számértéket.
Letölthető fájl: tablak.txt.
Minta:
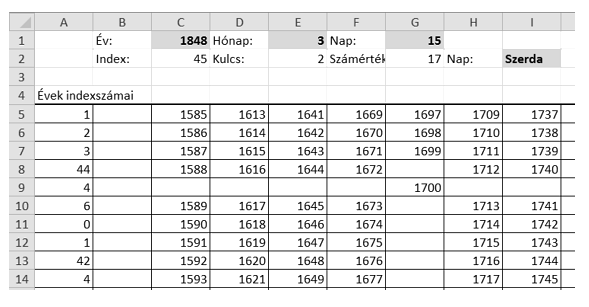
Beküldendő egy tömörített i380.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.
(10 pont)
I. 381. Készítsünk weblapot a HTML5 és CSS3 újdonságainak rövid bemutatására, természetesen a fenti szabványoknak megfelelő formában.
A kiinduló index.html oldal legyen olyan elrendezésű, hogy felül egy fejlécből, alul egy lábrészből és középen egy tartalomrészből álljon. A fejlécbe helyezzünk el a témához illő logókat bal oldalon, mellette jelenjen meg a ,,HTML5 -- CSS3 újdonságok és érdekességek'' cím. A tartalom részben 300 px széles, azonos magasságú dobozok legyenek, amelyek egy-egy újdonságot mutatnak be. A nyolc doboz mindegyike egy azonos méretű képet és egy mondatot tartalmazzon, valamint legyen hivatkozás egy olyan weboldalra, ahol a témát bővebben kifejtik. Ezek között legyen egy olyan doboz, amelynek témáját a kedvenc.html oldalon mi magunk magyarázzuk el, az oldalon működő példával. A kedvenc.html oldal szerkezete legyen a főoldalhoz hasonló, de a tartalom rész egy dobozában helyezzük el a kedvenc újdonság leírását. A lábrészt impresszumként használjuk föl, ahol adjuk meg adataink (név, évfolyam, iskola, város) és a HTML5 és CSS3 ellenőrzés logókat.
A két oldal kinézetét és elrendezését egy közös forma.css állomány segítségével adjuk meg. A weboldal különböző méretű megjelenítőkön is jól nézzen ki, tehát a megjelenítő szélességétől függően másként rendezzük el az oldalt. Egyrészt a fejléc és lábléc logói csak közepes és nagyobb megjelenítőkön legyenek láthatóak, de a szövegek minden betűje mindig jelenjen meg. Másészt a főoldal dobozai egymástól egyenlő távolságban legyenek elrendezve, a legnagyobb megjelenítőkön egy sorban négy, majd fokozatosan kevesebb, míg a legkisebbeken soronként egy. Az oldal színvilága a szürke árnyalataira épüljön, más színt csak a képeknél használjunk.
Beküldendő egy tömörített i381.zip állományban a weboldalt tartalmazó mappa.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
I/S. 1. Egy kisfeszültséggel működő áramkörben egy vékony fémlemez van, amelyből egy automata körlemezeket vág ki. Feladatunk annak eldöntése, hogy az áramkör zárt marad-e a körlemezek eltávolítása után, van-e kontaktus az \(\displaystyle A\) és a \(\displaystyle B\) pont között.

A fémlemez \(\displaystyle N\times M\) (\(\displaystyle 10\le N,M\le 1000\)) téglalap alakú, amelyből \(\displaystyle K\) (\(\displaystyle 0\le K\le 100\)) kört vágunk ki. A körök metszhetik egymást, középpontjaik (\(\displaystyle x_{i}\), \(\displaystyle y_{i}\) egészek) a lemezen belül vannak, és a sugaraik (\(\displaystyle 0 < r_{i} \le \min(N,M)\)) ismert egészek. A fémlemez \(\displaystyle N\) hosszú és \(\displaystyle M\) széles, az \(\displaystyle A\) pont az \(\displaystyle x=0\), míg a \(\displaystyle B\) pont az \(\displaystyle x=N\) helyen kapcsolódik a fémlemezhez (vagyis a lemez teljes oldalsó szélével össze vannak kötve). A körök kivágása a körlemez és kerületének eltávolításával jár, tehát az éppen érintkező körök érintkezési pontjai sem maradnak a fémlemezen.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et, \(\displaystyle M\)-et és \(\displaystyle K\)-t, majd a következő \(\displaystyle K\) sorból a körök középpontjainak koordinátáit és sugarait (nemnegatív egészek), majd írja a standard output első és egyetlen sorába a ,,Vezet'' vagy ,,Nem vezet'' szavakat attól függően, hogy az áramkör zárt maradt-e a körök eltávolítása után.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített is1.zip állományban a program forráskódja és dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
S. 100. Adott \(\displaystyle N\) (\(\displaystyle 1\le N\le 300\;000\)) db négyzet, melyek oldalai párhuzamosak a koordináta-rendszer tengelyeivel. Minden négyzet pontosan \(\displaystyle K\times K\)-as méretű, ahol (\(\displaystyle 1\le K\le 1\;000\;000\)). Adottak a négyzetek középpontjai az \(\displaystyle (x; y)\) koordinátákkal (\(\displaystyle -1\;000\;000\le x, y\le 1\;000\;000\)). Optimális esetben a négyzetek nem lógnak egymásba, viszont előfordulhat, hogy egy vagy több négyzetpárnak mégis van közös területe.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et, \(\displaystyle K\)-t, majd a következő \(\displaystyle N\) sorból a középpontokat: \(\displaystyle x_i\), \(\displaystyle y_i\), majd írjon a standard output első és egyetlen sorába: 0, t, ha nincs egymásba lógó négyzetpár, -1-et, ha több négyzetpár is egymásba lóg és a közös terület nagyságát, ha pontosan egy négyzetpár lóg egymásba.

Magyarázat: az 1-es és a 3-as négyzetek lógnak egymásba.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített s100.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

