A KöMaL 2015. szeptemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
K. 463. Egy pénzösszeget négy ember között osztottak szét. Az első 3000 Ft-tal többet kapott, mint a teljes összege harmada, a második 6000 Ft-tal többet kapott, mint a teljes összeg negyede, a harmadik 9000 Ft-tal többet kapott, mint a teljes összeg ötöde, a negyedik pedig 12000 Ft-tal többet, mint a teljes összeg hatoda. Hány forint volt a teljes összeg?
(6 pont)
K. 464. Az iskolában a tanár azt a feladatot adta, hogy 1-től 1000-ig számoljanak el a tanulók. Egy számítási lépés során kétféle dolog közül választhatnak: az éppen aktuális eredményüket megszorozzák egy általuk előre kiválasztott egyjegyű \(\displaystyle a\) számmal, vagy hozzáadnak 1-et. Melyik számot válasszuk \(\displaystyle a\)-nak, hogy a lehető legkevesebb lépésben teljesítsük a feladatot?
(6 pont)
K. 465. Egy kincsesláda elektronikus zárszerkezetét nyolc darab kis kapcsoló vezérli. Minden kapcsoló kétféle állásban lehet, felfelé vagy lefelé kapcsolva. A zár akkor nyílik ki, ha minden kapcsoló felfelé áll. Bármelyik kapcsolót átkapcsolhatjuk egyik állásából a másikba. Egy automatika azonban érzékeli, hogy melyik kapcsoló állásán változtattunk, és azonnal három másik kapcsolót is átkapcsol az aktuális állásából az ellenkező állásba. (Az automatika által átkapcsolt kapcsolók továbbiakat már nem fordítanak át.) Az alábbi táblázatban találhatjuk, hogy melyik kapcsoló állásának megváltoztatásakor melyik három kapcsoló állása változik meg (az egyszerűség kedvéért megszámoztuk a kapcsolókat).
|
\(\displaystyle a)\) Kezdetben minden kapcsoló lefelé áll, kivéve a 6-ost és a 7-est. Ebből a helyzetből indulva két kapcsoló átkapcsolásával ki tudjuk nyitni a ládát. Melyik két kapcsolót kell használnunk?
\(\displaystyle b)\) Kezdetben minden kapcsoló lefelé áll, kivéve a 7-est. Ebből az állásból indulva kinyitható-e a láda a kapcsolók segítségével?
(6 pont)
K. 466. Hány olyan egész szám van 1-től 2015-ig, melynek 10-es számrendszerbeli alakjában van 5-ös, de nincs 7-es számjegy?
(6 pont)
K. 467. Legyen\(\displaystyle p\) egy 3-nál nagyobb és 1000-nél kisebb prímszám. Mekkora az esélye, hogy \(\displaystyle p - 1\) vagy \(\displaystyle p +1\) osztható 6-tal?
(6 pont)
K. 468. A \(\displaystyle \frac{30-x}{91}\) egyszerűsíthető törtben az \(\displaystyle x\) pozitív egész számot jelöl. Adjuk meg a tört összes lehetséges értékét egyszerűsített alakban!
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
C. 1301. Bizonyítsuk be, hogy ha \(\displaystyle x_1\) és \(\displaystyle x_2\) pozitív valós számok, akkor
\(\displaystyle (x_1+x_2+1) \left(\frac{1}{x_1}+\frac{1}{x_2}+1\right)\ge 9. \)
(5 pont)
C. 1302. Adott egy \(\displaystyle O\) középpontú, \(\displaystyle r\) sugarú kör, és rajta kívül egy \(\displaystyle P\) pont. A \(\displaystyle P\)-ből húzott érintők érintési pontjai a körön legyenek \(\displaystyle Q\) és \(\displaystyle R\). Mekkora legyen az \(\displaystyle |OP|\) távolság, hogy a \(\displaystyle PQOR\) négyszög területe megegyezzen a kör területével?
(5 pont)
C. 1303. Egy \(\displaystyle 130~\rm{cm}^2\) területű, téglalap alakú origami papír két szomszédos csúcsát szimmetrikusan középre hajtottuk úgy, hogy a középre hajtott két oldal szabályos háromszöget formáz az ábra szerint. Mekkorák az eredeti papírlap oldalai?
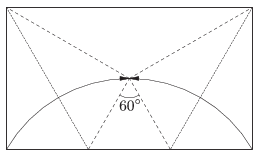
(5 pont)
C. 1304. Két játékos felváltva felír a táblára egy-egy természetes számot 1-től 10-ig. A szabály szerint csak olyan számot írhatnak fel, amely a táblán lévő számok egyikének sem osztója. Az a játékos veszít, aki a soron következő lépését nem tudja megtenni. Mutassuk meg, hogy ha a kezdő játékos jól játszik, akkor biztosan nyer.
(5 pont)
C. 1305. Egy \(\displaystyle n\) egység oldalú négyzetből spirált készítünk az ábrán látható módon úgy, hogy a négyzet csúcsából indulva, befelé haladva mindig egy egységgel azelőtt törjük meg a vonalat, minthogy az belemetszene a spirál már meglévő részébe. Hasonló módon az \(\displaystyle 1{,}8n\) egység oldalú szabályos háromszögből képzett spirálnál a metszéspontot mindig \(\displaystyle 1{,}8\) egységgel előzzük meg. (Az ábra \(\displaystyle n=4\) esetén mutatja a két spirált.) Milyen \(\displaystyle n\) érték mellett lesz a két spirál hossza megegyező?
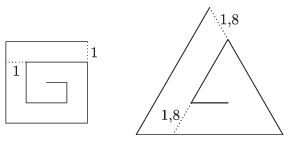
(5 pont)
C. 1306. Bizonyítsuk be, hogy ha egy háromszögben két oldal is legfeljebb akkora, mint a hozzájuk tartozó magasság, akkor a háromszög egyenlő szárú derékszögű háromszög.
(5 pont)
C. 1307. Milyen \(\displaystyle q\) valós számra lesznek a \(\displaystyle \big(3-\sqrt{5}\,\big)\), \(\displaystyle \Big(\frac{3\sqrt{5}}{5}-q\Big)\), \(\displaystyle \Big(0,6-\frac{1}{\sqrt{5}}\Big)\) számok egy mértani sorozat egymást követő szomszédos elemei?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
B. 4723. Megadható-e végtelen sok különböző prímszám, melyek közül bármely 2015 összege összetett szám?
Javasolta: Mészáros Gábor (Budapest)
(3 pont)
B. 4724. Oldjuk meg és ábrázoljuk az
\(\displaystyle x+y-xy+\frac{1}{x} +\frac{1}{y} -\frac{1}{xy}\le 2 \)
egyenlőtlenséget.
(4 pont)
B. 4725. Mutassuk meg, hogy ha egy egyszerű gráfnak 7 csúcsa van és nincs 4 hosszú köre, akkor van olyan csúcsa, aminek a foka legfeljebb 2.
(4 pont)
B. 4726. Az \(\displaystyle ABCD\) négyzet \(\displaystyle AB\), illetve \(\displaystyle BC\) oldalán lévő \(\displaystyle P\), illetve \(\displaystyle Q\) pontra \(\displaystyle BP=BQ\). Jelölje \(\displaystyle T\) a \(\displaystyle B\) csúcsból a \(\displaystyle PC\) szakaszra bocsátott merőleges talppontját. Bizonyítsuk be, hogy a \(\displaystyle DTQ\sphericalangle\) derékszög.
(4 pont)
B. 4727. Határozzuk meg az összes olyan \(\displaystyle f:\mathbb R \to \mathbb R\) függvényt, amelyre tetszőleges \(\displaystyle x\), \(\displaystyle y\)-ra \(\displaystyle f(x+y)+f(x)f(y)=x^2 y^2+2xy\).
(5 pont)
B. 4728. Legyen \(\displaystyle e\) egy kocka valamelyik élegyenese. Hány olyan egyenes van a térben, ami a kocka 12 élegyenese közül pontosan azokat metszi, amelyek \(\displaystyle e\)-hez képest kitérők?
(3 pont)
B. 4729. Adott az \(\displaystyle ABCD\) négyszög, melynek \(\displaystyle C\)-nél és \(\displaystyle D\)-nél levő szöge derékszög. Szerkesszük meg a \(\displaystyle CD\) szakasznak azt a \(\displaystyle P\) pontját, melyre \(\displaystyle APD \sphericalangle= 2 \, BPC \sphericalangle\).
(5 pont)
B. 4730. Adottak a síkon az egymást \(\displaystyle E\)-ben érintő \(\displaystyle k_1\) és \(\displaystyle k_2\) körök. Kijelöltük mindkét \(\displaystyle k_i\) körön (\(\displaystyle i = 1, 2\)) az \(\displaystyle X_i\) és \(\displaystyle Y_i\) pontot úgy, hogy a két \(\displaystyle X_iY_i\) egyenes a körök közös belső érintőjén messe egymást. Bizonyítsuk be, hogy az \(\displaystyle X_1X_2E\) és \(\displaystyle Y_1Y_2E\) körök centrálisa, valamint az \(\displaystyle X_1Y_2E\) és \(\displaystyle X_2Y_1E\) körök centrálisa szintén a közös belső érintőn metszi egymást.
Javasolta: Williams Kada (Szeged, Radnóti M. Gimn.)
(5 pont)
B. 4731. Legyen \(\displaystyle 0\le a,b,c \le 2\), és \(\displaystyle a+b+c=3\). Határozzuk meg
\(\displaystyle \sqrt{a(b+1)} + \sqrt{b(c+1)} + \sqrt{c(a+1)} \)
legnagyobb és legkisebb értékét.
Javasolta: Williams Kada (Szeged, Radnóti M. Gimn.)
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2015. október 12-én LEJÁRT. |
A. 647. Legyen \(\displaystyle k\) nemnegatív egész szám. Bizonyítsuk be, hogy csak véges sok \(\displaystyle n\) pozitív egész esetén léteznek olyan diszjunkt \(\displaystyle A\) és \(\displaystyle B\) halmazok, amelyekre \(\displaystyle A \cup B = \{1; 2; \ldots; n\}\) és \(\displaystyle \displaystyle\left|\prod \limits_{a \in A} {a} - \prod\limits _{b \in B} {b}\right|=k\) teljesül.
Javasolta: Maga Balázs, Budapest
(5 pont)
A. 648. Az \(\displaystyle ABC\) hegyesszögű háromszög \(\displaystyle BC\), \(\displaystyle CA\) és \(\displaystyle AB\) oldalainak felezőpontjai rendre \(\displaystyle D\), \(\displaystyle E\), illetve \(\displaystyle F\). A háromszög \(\displaystyle C\) pontból induló magasságának talppontja \(\displaystyle T_1\). Egy, a \(\displaystyle C\) ponton áthaladó, de a \(\displaystyle T_1\) pontra nem illeszkedő egyenesen az \(\displaystyle A\)-ból és \(\displaystyle B\)-ből bocsátott merőlegesek talppontjai \(\displaystyle T_2\), illetve \(\displaystyle T_3\). Bizonyítsuk be, hogy a \(\displaystyle DEF\) kör átmegy a \(\displaystyle T_1T_2T_3\) kör középpontján.
Javasolta: Bíró Bálint, Eger
(5 pont)
A. 649. Egy konvex poliédernek minden lapja négyszög. Mutassuk meg, hogy a poliéder lapjait háromszögekre bonthatjuk egy-egy átló meghúzásával úgy, hogy a poliéder minden csúcsánál páros számú háromszög találkozzon.
Javasolta: Nagy János, Budapest
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

