KöMaL Problems in Physics, October 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on November 10, 2015. |
M. 353. Stick a coin (or several coins) with a piece of cello-tape onto the hole at the middle of a damaged or not used CD disc. (Put cello-tape to the other side of the hole as well in order to make the rim of the small hole smooth.) Carefully place the disc onto the surface of water in a dish - such that the coin is at the bottom of the disc - and from a certain height pour water onto the hole of the disc. The water beam should be narrow and vertical. If the water beam is strong enough (but not too strong) then the CD disc does not sink when it is released.
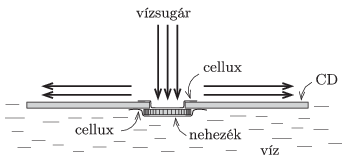
Measure how the minimum amount of water needed for the floating of the disc depends on the total mass of the disc-coin system.
(6 pont)
 |
Problems with sign 'P'Deadline expired on November 10, 2015. |
P. 4758. A piece of wire is to be used to make an immersion heater rated at 230 V, and 300 W. What should the length of the wire be, if the cross section of the wire is \(\displaystyle 0.1~{\rm mm}^2\), and its resistivity is \(\displaystyle 1.6~\Omega\;{\rm mm}^2/{\rm m}\)?
(3 pont)
P. 4759. What should the angle between two forces be, if the magnitude of their sum is the same as the geometric mean of the magnitudes of the forces? Under what conditions will this angle be minimum, and what is this minimum value?
(4 pont)
P. 4760. The speed of a car travelling on a highway is \(\displaystyle v_0\). At a certain instant the speed of the car is started to vary uniformly, and from that instant the first 84 m is covered in 3 s, and the next 84 m is covered in 4 s.
Determine the initial speed of the car \(\displaystyle v_0\), and its acceleration \(\displaystyle a\).
(4 pont)
P. 4761. The acceleration of a strange car is inversely proportional to its speed in the speed interval of \(\displaystyle (v_1,v_2)\), so \(\displaystyle a=A/v\) (\(\displaystyle A\) is a positive constant).
\(\displaystyle a)\) How long does it take for the car to speed up from the speed \(\displaystyle v_1\) to the speed \(\displaystyle v_2\)?
\(\displaystyle b)\) What is the power of the car during this motion?
(4 pont)
P. 4762. A piece of iron is attached to the bottom of a wooden cylinder of cross section \(\displaystyle A_0\), so the wooden cylinder is floating in a sample of liquid of density \(\displaystyle \varrho_1\), which liquid is in a beaker of cross-section \(\displaystyle A_1\). The beaker is also floating in some liquid of density \(\displaystyle \varrho_2\), in another bigger beaker of cross section \(\displaystyle A_2>A_1\). This beaker is also floating in some liquid of density \(\displaystyle \varrho_3\) in another even wider beaker of cross-section \(\displaystyle A_3>A_2\), and so on...\(\displaystyle \,\). Altogether there are \(\displaystyle n\) beakers on the table. The symmetry axes of all beakers and the wooden cylinder are vertical.
Then the wooden cylinder is pushed down by a vertical force of \(\displaystyle F\). (Neither the wooden cylinder nor any of the beakers touch the other beaker below them.)
\(\displaystyle a)\) By what amount did the height of immersed part of the wooden cylinder in the first liquid increase?
\(\displaystyle b)\) By what amount did the level of the liquid in the first liquid increase?
\(\displaystyle c)\) By what amount did the level of the liquid in the \(\displaystyle i\)-th beaker increased?
(5 pont)
P. 4763. A light-ray entering into a glass cube through one of the faces of the cube is reflected from three faces of the cube. The common point of these three faces is one of the vertices of the cube. Then the reflected light-ray emerges from the same face of the cube as it entered into it.
What can be stated about the direction of the emerging light-ray?
(4 pont)
P. 4764. The resistance of each resistor shown in the figure is the same \(\displaystyle R\). By what percent will the dissipated power at resistor (1) change if switch K is turned on to create a short circuit through the resistor (2)?
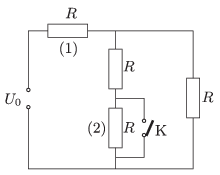
(4 pont)
P. 4765. A coil of inductance 250 mH, and of resistance 0.3 \(\displaystyle \Omega\) is connected to a battery of constant terminal voltage. How much time elapses until the current through the coil reaches
\(\displaystyle a)\) 50% of the stationary final value;
\(\displaystyle b)\) 75% of the stationary final value?
(4 pont)
P. 4766. An aluminium sheet is illuminated by ultraviolet light of wavelength 200 nm.
\(\displaystyle a)\) what will the kinetic energy of the fastest and the slowest emitted electrons?
\(\displaystyle b)\) What is the stopping voltage?
(4 pont)
P. 4767. Several small holes are drilled into the wall of a cylinder shaped container. The symmetry axis of the cylinder is vertical. The container is filled with water up to a height of \(\displaystyle H\), and due to this, narrow beams of water flow out of the container (perpendicularly to the wall of the cylinder). What is the shape of the envelope of the beams of water? (The water beams do not form obstacles to each other, and the water level in the container is kept constant by refilling the water.)
(6 pont)
Upload your solutions above.
