KöMaL Problems in Informatics, November 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on December 10, 2015. |
I. 385. The Playfair cipher (Source: \(\displaystyle {\rm https://en.wikipedia.org/wiki/Playfair\_cipher} \)) was invented by Charles Wheatstone in 1854, but he named it after his friend Lord Playfair who made the method popular. The encryption scheme itself had been broken before World War I, although Australians still used it in World War II (because computers were not yet available, and by the time that the enemy could break the message, the information would be useless to them).
The encryption scheme is based on a \(\displaystyle 5\times 5\) table containing the letters of the English alphabet-this alphabet has 26 letters, so we need to discard one letter, say, Q. The table is known only to the sender and the receiver.
The text to be encrypted (in our example FINOM IZ) is first partitioned into consecutive pairs of letters. If necessary, a new symbol (in our case X) is appended at the end. We proceed similarly if the original text contains a double letter in a pair: for example, AA is converted into AX AX.
During the encryption process, each pair of letters is replaced by another pair according to the following rules.
\(\displaystyle \bullet\) If both letters of the original pair are in a single row, then take the corresponding right neighbor in the table for each letter. The right neighbor of the last letter in a row is the first letter of the same row (FI \(\displaystyle \to\) RN).
\(\displaystyle \bullet\) If both letters of the original pair are in a single column, then take the corresponding lower neighbor in the table for each letter. The lower neighbor of the last letter in a column is the first letter of the same column (NO \(\displaystyle \to\) VN).
\(\displaystyle \bullet\) Finally, if the two letters of the original pair are found in different rows and columns, then we consider the rectangle whose diagonal is formed by these two letters. Letters of the new pair will be given by letters of the other diagonal of the rectangle, by keeping the same row for a letter (MI \(\displaystyle \to\) KF).

The first command-line argument of your program is either a character R or character V to denote whether the user wants to encrypt or decrypt data. The second argument is the input file name containing the Playfair table (read from left to right and top to bottom), the third argument is the input file name containing the text to be encrypted or decrypted, and the fourth argument is the output file name.
You can assume that the input text contains only uppercase letters of the English alphabet according to the above. Your program should be able to handle large (several GB in size) input or output files.
The source code and documentation of your program-containing a brief description of your solution, and the name of the developer environment to compile your code-should be submitted in a compressed file i385.zip.
Downloadable files (a possible Playfair table, and a sample original text file): kod.txt, be.txt.
(10 pont)
I. 386. A certain school in Hungary bears the name of the Hungarian poet Gyula Juhász (1883-1937). Since the beginning of the 2011 school year they select a poem of Juhász every day and display it on the webpage of the school. Visitors can ``like'' these poems. The database contains data from three consecutive school years.
Create a new database jgy. The two, tabulator-separated and UTF-8 encoded text files (vers.txt, napverse.txt) should be imported into the database by using their original names (vers, napverse). The first line of the file contains the field names. The appropriate types and keys should be set.
Tables:

You should solve the following tasks and save your queries by using the names in parentheses. Your solution should contain only the requested fields.
1. List all poems that appeared on the webpage in September 2011 and sort them according to their dates. Display the poem title and creation year. (2szept)
2. Consider the poems which appeared more than once on the webpage, and determine which three got the most ``likes''. (3like)
3. Create a report to list the poems that appeared on the webpage during the winter of 2013/2014 (between December and February), grouped according to their creation year and sorted alphabetically. (4tel)
4. Determine which poems appeared on the webpage in all four calendar years. (5negyev)
5. Determine which poems appeared on the webpage only in 2011. (6csak2011)
6. Determine which days had poems with creation year identical to the creation year of the poem of the previous day. (7azonosev)
7. Determine whether Juhász created more poems in his first or last active decade. The first year of the more active decade should be displayed. (8evtized)
Your solution as a database or a text file with the SQL queries should be submitted in a compressed file (i386.zip), also containing a short documentation with the name and version number of the database application.
Downloadable files: vers.txt , napverse.txt.
(10 pont)
I. 387. Converting Roman numerals to Arabic numbers was the topic of the spreadsheet management task of the practical part of the advanced level Matriculation Examination in Informatics in Hungary in May 2012. The algorithm given there can also be realized by using functional programming.
By using a Logo program and the given algorithm, convert Roman numerals to Arabic numbers. You can assume that the input Roman numerals (between 1 and 4000, and described by at most 20 capital letters) are syntactically correct.
The conversion algorithm is described below.
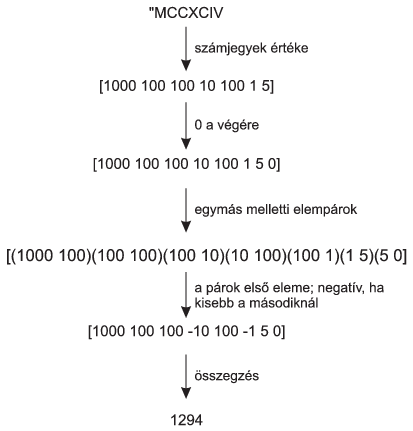
Here ``a számjegyek értéke'' is the ``values of the numerals''; ``0 a végére'' is ``appending 0 at the end''; ``az egymás melletti elempárok'' is ``adjacent pairs''; ``a párok első eleme'' is ``the first entries of the pairs''; ``negatív, ha kisebb a másodiknál'' is ``negative if the first entry is smaller than the second one''; and ``összegzés" is ``summation''.
The sign of a given numeral is negative if the following numeral is larger. The value of the last numeral is always positive.
Create the Logo words corresponding to the above steps of the algorithm, then the word római_tízes performing the actual conversion.
|
Only the automatic and functional features of the programming language should be used in your solution; variables should not be used just parameterizations.
The project file/source code of your program should be submitted (i387.imp).
(10 pont)
 |
Problems with sign 'I/S'Deadline expired on December 10, 2015. |
I/S. 3. One can buy \(\displaystyle 1\le N\le 1000\) items in a shop. Your available money is \(\displaystyle 1\le P \le 10^9\).
Each item has a price \(\displaystyle A_i\), and a home delivery cost \(\displaystyle H_i\), so the total cost of item \(\displaystyle i\) is \(\displaystyle A_i+H_i\) (non-negative integers, \(\displaystyle A_i\) is even to simplify this exercise). We also have a coupon to halve the price of a selected item: if we use it with item \(\displaystyle i\), then its price would be \(\displaystyle A_i/2+H_i\). Determine the maximum number of items that can be bought if we are allowed to use only one coupon. Your program should read the values of \(\displaystyle N\) and \(\displaystyle P\) from the first line of the standard input, then the integers \(\displaystyle A_i\), \(\displaystyle H_i\) (separated by a space) from the following \(\displaystyle N\) lines. The first and only line of the standard output should contain the maximum number of items that can be purchased.

Explanation: it is possible to buy the first 4 items provided that the coupon is used with the third item.
Scoring and bounds. You can get 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any valid input within 1 second of running time.
The source code of your program without the .exe or any other auxiliary files generated by the compiler but with a short documentation-also describing which developer environment to use for compiling the source-should be submitted in a compressed file is3.zip.
(10 pont)
 |
Problems with sign 'S'Deadline expired on December 10, 2015. |
S. 102. A certain robot is controlled by the following commands: it starts from position 0, then upon receiving 15 R and 20 L, for example, it makes 15 steps to the right then 20 steps to the left. The robot receives \(\displaystyle N\) commands (\(\displaystyle 1\le N\le 300\;000\)). The step numbers appearing in these R/L commands are positive integers, and the maximum allowed distance of the robot from the origin is \(\displaystyle 10^{9}\). You are also given a number \(\displaystyle K\). Your task is to determine the number of positions on or over which the robot passed at least \(\displaystyle K\) times.
Your program should read the values of \(\displaystyle N\) and \(\displaystyle K\) from the first line of the standard input, then the \(\displaystyle a_i\), \(\displaystyle c_i\) number-character pairs (separated by a space) from the following \(\displaystyle N\) lines describing the motion of the robot. The first and only line of the standard output should contain the appropriate number of positions the robot visited.

Scoring and bounds. You can get 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any valid input within 1 second of running time.
The source code of your program without the .exe or any other auxiliary files generated by the compiler but with a short documentation---also describing which developer environment to use for compiling the source---should be submitted in a compressed file s102.zip.
(10 pont)
$Var(Body)
Upload your solutions above
