KöMaL Problems in Physics, December 2015
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 11, 2016. |
M. 355. Drop some cooking oil onto the surface of water. How does the diameter of the oil spot depends on the amount of the oil?
(6 pont)
 |
Problems with sign 'P'Deadline expired on January 11, 2016. |
P. 4780. At which latitude should we stand in order that we could observe (by means of a good quality telescope) a geostationary ``synchronous satellite''?
(3 pont)
P. 4781. 200 g water is heated on a camping stove from a temperature of \(\displaystyle 15~{}^\circ\)C to a temperature of \(\displaystyle 75~{}^\circ\)C. (The cartridge of the stove contains 80% butene and 20% propane.)
By what amount does the total mass of the stove change during the heating process, if the efficiency of heating is 60%?
(3 pont)
P. 4782. One end of a 16 cm-long and a 30 cm-long pieces of rope are attached to the ceiling at a distance of 34 cm. The other ends of the ropes are attached to a small object of mass 17 grams.
\(\displaystyle a)\) Calculate the tensions in the ropes.
\(\displaystyle b)\) The shorter rope is burnt. What is the tension in the other rope when it is vertical?
(4 pont)
P. 4783. A wedge of mass \(\displaystyle m_1\), and a cube of mass \(\displaystyle m_2\) on the horizontal face of the wedge are sliding down along an inclined plane of angle of elevation of \(\displaystyle \alpha=30^\circ\) at the same acceleration. The coefficient of friction between the wedge and the inclined plane is 0.1.
What is the minimum value of the frictional coefficient between the wedge and the cube, if the cube does not slip on the wedge?
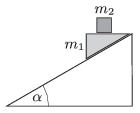
(4 pont)
P. 4784. The parabolic mirror of the Canadian Large Zenith Telescope is created by a uniformly spinning pan filled with liquid mercury. The diameter of the telescope is 6 m, and the number of revolutions of the pan is 8.5/minutes.
Determine the focal length of the parabolic mirror.
(4 pont)
P. 4785. The Milky Way is a so called spiral galaxy. Its shape is approximately a uniform density disc which has a small width with respect to its diameter. The Sun undergoes simple harmonic motion between the ``bottom'' and the ``top'' of this disc.
What is the period of the SHM, if the average density of the galaxy is \(\displaystyle 5.8\cdot 10^{-21}~{\rm kg/m}^3\)?
(5 pont)
P. 4786. There are three point-like objects in space - far from any other objects - such that their initial velocities are zero, and the distance between any two is the same \(\displaystyle d\). Two of the objects have the same mass of \(\displaystyle m\), and the mass of the third one is \(\displaystyle 2m\). Due to the gravitational force the objects begin to move and they collide with each other.
\(\displaystyle a)\) How much distance do they cover until they meet?
\(\displaystyle b)\) How much time elapses until the collision of the objects?
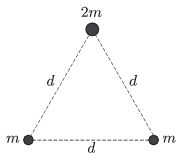
(5 pont)
P. 4787. There is a sample of \(\displaystyle 17~{}^\circ\)C Helium gas in a container of rigid adiabatic walls. The container is dropped to the surface of the Moon from a height of 30 m.
\(\displaystyle a)\) What will the ordered speed of the Helium atoms be, at the impact of the container?
\(\displaystyle b)\) By what amount does the unordered thermal average speed of the Helium atoms increase after the impact?
(4 pont)
P. 4788. The measure of current flowing in each of three long straight wires through every other vertex of a regular hexagon of edges \(\displaystyle a=2\) cm is \(\displaystyle I=10\) A. Each wire is perpendicular to the plane of the hexagon, and the direction of the current in two of the wires is upward, whilst in the third wire the current flows downward.
\(\displaystyle a)\) What is the magnitude and the direction of the magnetic induction at the centre of the hexagon?
\(\displaystyle b)\) What is the magnitude and the direction of the force exerted on a \(\displaystyle \ell=1\) m long piece of each wire?
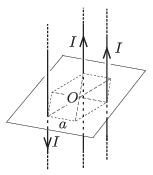
(4 pont)
P. 4789. We would like to solder a so called Sierpinski-triangle from a piece of thin wire of uniform cross-section. We start from an equilateral triangle shaped frame, in which the resistance measured between the the vertices \(\displaystyle A\) and \(\displaystyle B\) is \(\displaystyle R_0\). First the wires at the midlines of the triangle are soldered to the original frame, and then the second step is to solder the wires along the midlines of three outer triangles which were created. The process is continued similarly, and a fractal like frame is created (see the figure).
What will the resistance between the points \(\displaystyle A\) and \(\displaystyle B\) be after the \(\displaystyle n\)-th step?
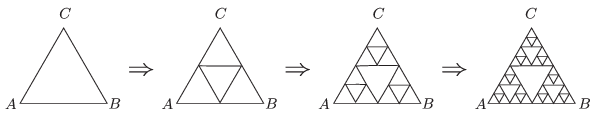
(5 pont)
P. 4790. The refractive index of the material of a triangular prism of apex angle \(\displaystyle \varphi=45^\circ\) is \(\displaystyle n_1=1.3\). The base of the prism is an isosceles triangle of height \(\displaystyle H=20\) cm. Another prism of apex angle \(\displaystyle \varphi/2\) is attached to the previously described one as shown in the figure. A beam of light enters to the first prism, parallel to the base of the isosceles triangle at a distance of \(\displaystyle h=12~\)cm from it.
\(\displaystyle a)\) What should the refractive index of the second prism \(\displaystyle n_2\) be in order that the light beam emerges parallel to the original beam?
\(\displaystyle b)\) By what distance \(\displaystyle d\) is the emerging beam displaced with respect to the entering ray?
\(\displaystyle c)\) How long does a wave-front of the light-beam take to travel through the double prism?
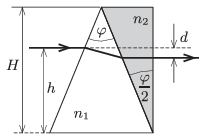
(5 pont)
P. 4791. Recently Peter's boiler makes very strange sounds, as if it would explode at any moment. A repairman was asked to have a look, and he said that limescale has deposited in the tube, and it must be descaled. Peter's small brother asked Peter how the strange sound could arise, and why the thermometer, which measures the temperature of the water, is scaled up to \(\displaystyle 120~{}^\circ\)C, since at that temperature the water would boil. What fraction of the tube is closed by the deposited scale?
What did Peter answer to these questions?
Data: The temperature of the water in the tube is \(\displaystyle 80~{}^\circ\)C, the pressure gauge reads 1.2 bar (excess) pressure, and at normal working conditions the pump makes the water flow at a speed of 3 m/s.
(6 pont)
Upload your solutions above.
