KöMaL Problems in Physics, January 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 10, 2016. |
M. 356. Measure the viscosity of honey at least at three different temperature values. Give the type of honey you used.
(6 pont)
 |
Problems with sign 'P'Deadline expired on February 10, 2016. |
P. 4792. Andrew claims that a plummet, or a pebble hanging at the end of a thread, everywhere points toward the centre of the Earth. According to Bertie, this never happens, the plummet, wherever it is, does not exactly point towards the centre of the Earth. Who is right?
(3 pont)
P. 4793. There is a sample of Argon in a 20-litre closed container at a pressure of 50 kPa, and there is a sample of Xenon in another container of volume of 30 litres at a pressure of 20 kPa. A tube (of negligible volume) connects the two containers, and the tap in it is opened. What will the pressure in the containers be if the temperature remains the original value?
(3 pont)
P. 4794. What percent of the kinetic energy of a spherical hailstone, falling in a hailstorm, is lost during the collision with the ground, if it bounces back to a height of 20 cm? The diameter of the hailstone is 6 mm.
(4 pont)
P. 4795. Peter and his friend Norbert are discussing, that if the Earth was closer to the Sun, more energy from the Sun would be available for us. Finally they are arguing about the question on which planet would more energy be available if the surface of both the Earth and Mercury were wrapped with photovoltaic cells. According to Peter on the Earth, since it is much greater, and according to Norbert on the Mercury, because it is much closer to the Sun. Which of them is right?
(4 pont)
P. 4796. Two simple pendulums of the same length are suspended at the same point. One of the pendulum bobs is an iron ball of mass 78-g and the other one is a 12-g ball made of modelling clay. The pendulums are displaced such that the angle between the threads is \(\displaystyle 60^\circ\), and
\(\displaystyle a)\) the angles between the threads and the horizontal are also \(\displaystyle 60^\circ\);
\(\displaystyle b)\) the angles between the threads and the vertical are also \(\displaystyle 60^\circ\).
The two bobs are released at the same instant without any initial speed. The two bobs collide and stick to each other. What is the angle between the threads and the vertical when the two bobs are at the highest point?
(5 pont)
P. 4797. A sample of ideal gas (of constant mass) is taken from state \(\displaystyle A\) to state \(\displaystyle C\) through the semi-circle shaped processes named \(\displaystyle ABC\) and \(\displaystyle ADC\) as shown in the figure.
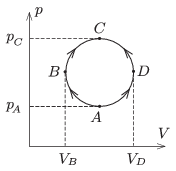
\(\displaystyle a)\) In which case will the algebraic sum of the absorbed heat and the released heat be the greater?
\(\displaystyle b)\) By what amount is it greater?
(4 pont)
P. 4798. In a region of uniform, vertically upward electric field the magnitude of the electric field strength is \(\displaystyle E\). In this field there are two fixed charges of charge \(\displaystyle -Q\) at a distance of \(\displaystyle 2a\) along a horizontal line. At the midpoint of the line segment between the two charges there is a small bead on a vertical thread (as shown in figure \(\displaystyle a)\)). The charge on the bead is \(\displaystyle q>0\) and its mass is \(\displaystyle m\). The bead is released from rest. (It can move without friction along the thread.) When the bead reaches the furthest position from its starting point, the two charges and the bead will be at the vertices of an isosceles triangle of vertex angle \(\displaystyle 2\alpha=150^\circ\), as shown in figure \(\displaystyle b)\).
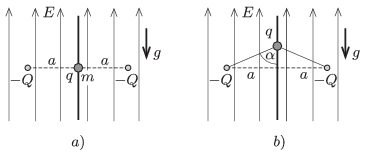
\(\displaystyle a)\) Find \(\displaystyle q\).
\(\displaystyle b)\) What will the greatest speed of the bead be?
\(\displaystyle c)\) What should the least initial speed given to the bead be, in order that it can reach any (distant) position?
Data: \(\displaystyle E=10^4\) N/C, \(\displaystyle a=10\) cm, \(\displaystyle Q=10^{-8}\) C, \(\displaystyle \alpha=75^\circ\), \(\displaystyle m=0.1\) g.
(5 pont)
P. 4799. The resistance of the resistor \(\displaystyle X\) shown in the figure can be any value.
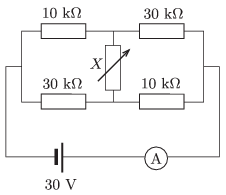
\(\displaystyle a)\) In what range can the reading on the ammeter change?
\(\displaystyle b)\) What is the resistance of \(\displaystyle X\) if the ammeter reads 1.6 mA?
(4 pont)
P. 4800. The electric current in a toroid of mean radius \(\displaystyle R\) is \(\displaystyle I_1\), and its number of turns is \(\displaystyle N_1\). A solenoid of radius \(\displaystyle r\) and of length \(\displaystyle \ell\) (\(\displaystyle \ell\gg R\)), is placed along the symmetry axis of the toroid. The number of turns of the solenoid is \(\displaystyle N_2\). In this coil the current is increased uniformly during a time of \(\displaystyle t_0\), until the magnetic field in the toroid
\(\displaystyle a)\) becomes zero;
\(\displaystyle b)\) becomes the opposite of the original magnetic field in the toroid.
Determine the electric field strength in the toroid along its mean radius in both cases.
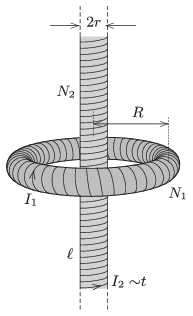
Data: \(\displaystyle R=20\) cm, \(\displaystyle N_1=300\), \(\displaystyle r=4\) cm, \(\displaystyle \ell=2\) m, \(\displaystyle I_1=0.5\) A, \(\displaystyle N_2=4000\), \(\displaystyle t_0=2\) s.
(5 pont)
P. 4801. The intensity of light scattered by the molecules of the atmosphere depends on some power of the wavelength. The intensity of light of wavelength 650 nm is one-quarter of the intensity of the light of wavelength 460 nm, -- this is why we observe that the sky is blue. What is the colour of that light for which it is true that when it scatters its intensity is half of the intensity of the scattered blue light of wavelength 460 nm?
(4 pont)
P. 4802. What is the least wavelength of the light which is emitted by a Hydrogen atom?
(3 pont)
P. 4803. A proton and an electron are travelling in magnetic field of magnetic induction of 1 T. The kinetic energy of both particles is 10 MeV, and their velocity is perpendicular to the magnetic induction. Determine the periods of their revolving motion.
(5 pont)
P. 4804. A uniform block of mass \(\displaystyle m\) is pulled along the horizontal tabletop as shown in the figure. One end of the thread is attached to the midpoint of the top horizontal edge (perpendicular to the plane of the figure) of the block. The thread is led through a pulley and its other end is pulled by a force \(\displaystyle F\), which is varied in order that the block moves at a constant speed. The coefficient of kinetic friction between the tabletop and the block is \(\displaystyle \mu\).
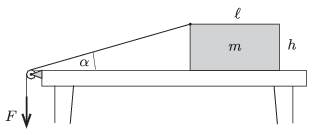
\(\displaystyle a)\) Determine how the tension in the thread depends on the angle \(\displaystyle \alpha\) shown in the figure.
\(\displaystyle b)\) What can the maximum value of this angle \(\displaystyle \alpha\) be while the block is sliding uniformly as prescribed above?
Data: \(\displaystyle \ell=17.3\) cm, \(\displaystyle h=11\) cm, \(\displaystyle mg=10\) N, \(\displaystyle \mu=0.15\).
(6 pont)
Upload your solutions above.
