A KöMaL 2016. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
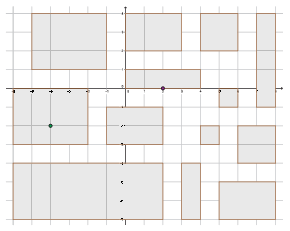
I. 394. A Birodalom kutasz droidja a Felkelőket keresi Nhalo városában. A város épületei téglalap alakúak, oldalaik párhuzamosak egymással. A droidot szállító egység egy megadott épületre száll le, ahol azonnal elkezdi a keresést. Először átvizsgálja a teljes épületet, majd az épülethez legközelebbi, egyik legkisebb épületben folytatja a keresést. Egy épület átvizsgálásának ideje az épület területével egyező időegységig tart. Miután végzett egy épülettel, ismét megállapítja, hogy a jelenlegi épülethez képest melyek a legközelebbi át nem vizsgált épületek, és azok közül az egyik legkisebbel folytatja a keresést. Ha több legkisebb épület van legközelebb, akkor a kutasz a legkisebb \(\displaystyle X\) koordinátával rendelkezőt választja, illetve egyenlő \(\displaystyle X\) koordináták esetén a legkisebb \(\displaystyle Y\) koordinátával bírót. A kutasz egyik épülettől a másikig a vizsgálat idejéhez képest elhanyagolható idő alatt ér át. Az épületek közötti távolság a két épület két egymáshoz legközelebbi pontjának/pontjainak távolsága.
A Felkelők a város egy adott épületében rejtőznek. Ismerik a fürkész droid kereső algoritmusát, és látják, hogy melyik épületre szállt le. Azonnal megkezdik a felkészülést a kiürítésre, de szeretnék tudni, hogy mennyi időegység áll rendelkezésükre. Mindenképp el kell indulniuk, mielőtt a droid az épületüket eléri. Számítsuk ki, hogy legföljebb mennyi idejük van a droid megérkezéséig.
A program a standard bemenetről olvassa be a város térképének adatait, valamint a Felkelők és a kutasz droid kiindulási helyét. (A standard I/O kezeléséről több feladat megoldása kapcsán is írtunk, a leírást tartalmazó stdio.pdf fájl honlapunkon elérhető pl. az S.64. feladat megoldásának végén.) A bemenet első sorában egy pozitív érték szerepel, amely megadja az épületek \(\displaystyle P\) számát (\(\displaystyle 2\le P\le 100\)). A bemenet következő \(\displaystyle P\) számú sorában az épületek derékszögű koordináta-rendszerben adott egész koordinátái szerepelnek, melyek értékei \(\displaystyle -100\) és \(\displaystyle +100\) közöttiek. A bemenet utolsó előtti sorában a kutasz droid leszállási helye, az utolsó sorában a Felkelők épületének egyik pontjának két koordinátája szerepel. A program adja meg a standard kimenet első sorába a kiürítésig biztosan rendelkezésre álló időt, a második sorban a droid által érintett épületek átvizsgálási idejét az előbbi időtartam mellett.
Példa (amelyben az újsor karakterek egy részét a tömörség kedvéért / jellel helyettesítettük):
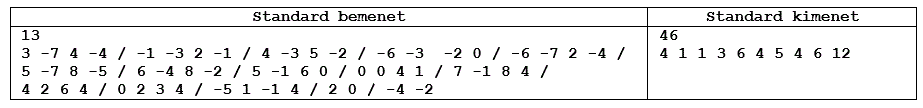
Beküldendő egy tömörített i394.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás vázlatos leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
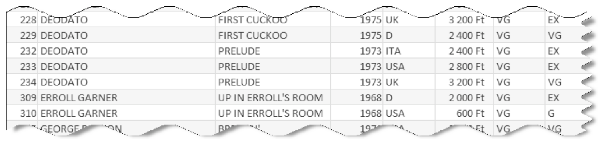
I. 395. (É). Egy régi hanglemezek kereskedelmével foglalkozó bolt jazz műfajú lemezeinek néhány adata áll rendelkezésünkre a lemeztar.txt, az ismerteto.txt és a skala.txt állományokban. Az állományok tabulátorral tagolt, UTF8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.
1. Készítsünk új adatbázist i395 néven. A fenti, honlapunkról letölthető adatállományokat importáljuk az adatbázisba a forrásállományokkal azonos néven.
2. Beolvasáskor állítsuk be a megfelelő adatformátumokat és kulcsokat. Az ismerteto táblába vegyünk fel kulcsmezőt, de ezen kívül a táblákba ne vegyünk fel további mezőket.
Táblák:

Készítsük el a következő feladatok megoldásait. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok ne. Megoldásainkat a zárójelben lévő néven mentsük el.
3. Soroljuk fel lekérdezés segítségével a német újraegyesítés előtt, a Német Demokratikus Köztársaságban (országkódja GDR) gyártott hanglemezek minden adatát. A listát ár szerint csökkenően rendezzük. (3ndk)
4. Készítsünk lekérdezést, amely megadja, hogy az 1960 és 1970 között (1960-at és '70-et is beleértve) gyártott lemezek közül melyik 3 országból származik a legtöbb. Eredményként az ország rövidítését adjuk meg. (4soklemez)
5. Legértékesebbek a még érintetlen hanglemezek. Lekérdezéssel határozzuk meg azoknak a hanglemezeknek az előadóját, címét és árát, amelyeknek a borítójához és a lemez állapotához a ,, bontatlan'' kifejezés is meg van adva az állapotánál. (5bontatlan)
6. Készítsünk jelentést, amely árakra lebontva megadja Oscar Peterson jazz zongorista önálló (egyedüli előadó) lemezeinek címét, kiadásuk évét és a lemez állapotának angol kifejezését. A jelentést lekérdezéssel készítsük elő. Az oszlopok felirata a mintának megfelelő legyen. (6peterson)

7. Sokáig nehéz volt lemezt készíteni Magyarországon és külföldön egyszerre. Lekérdezés segítségével adjuk meg azokat a Magyarországon (országkódja: H) lemezt kiadó előadókat, akiknek külföldön is készült lemeze. A listában minden név egyszer jelenjen meg. (7nemzetkozi)
8. Egy-egy jazz koncert felvételét több országban is kiadták egyszerre. Lekérdezés segítségével adjuk meg azoknak a lemezeknek minden adatát, amelyeknél az előadók, a címek, a kiadás éve megegyezik, de több országban is megjelentek. A listában minden lemez egyszer jelenjen meg. (8tobb)
Beküldendő egy tömörített i395.zip állományban az adatbázis, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott adatbázis-kezelő neve, verziószáma.
Letölthető fájlok: lemeztar.txt, ismerteto.txt, skala.txt.
(10 pont)
I. 396. A Scratch programozási nyelv és fejlesztői környezet segítségével nagyon könnyen szórakoztató játékokat készíthetünk. A rendszer alapismereteinek elsajátítása és felfedezése önmagában is érdekes, ugyanakkor a mások által készített programokkal is játszhatunk. Megnézhetjük belülről őket, vagyis tanulhatunk a programokból. Magyar nyelvű Scratch bevezető is elérhető a http://scratch.inf.elte.hu/ oldalon. A Scratch nemzetközi oldalán, a http://scratch.mit.edu webhelyen, regisztráció után mi magunk is készíthetünk és megoszthatunk programokat. A programozási nyelvben a vizuális elemek kezelése mellett, az egyes objektumok üzeneteket is tudnak küldeni egymásnak, illetve az objektumoktól függetlenül változók és listák kezelése is lehetséges.
Készítsük el a jól ismert kígyós játék egy változatát az alábbiak figyelembe vételével. A kígyó folyamatosan mozogjon vízszintesen vagy függőlegesen, feje a balra és jobbra nyilakkal forduljon az aktuális irányhoz képest \(\displaystyle 90^\circ\)-kal, a testének egyes szelvényei kövessék a fejet. A kígyó kezdetben a fejjel együtt öt testrészből álljon. A pályán induláskor véletlenszerű helyen és irányban jelenjen meg, és mozogjon öt ennivaló, amelyeket a kígyó a fejével meg tud enni. A kígyó hossza 10 másodpercenként eggyel csökkenjen, míg három ennivaló elfogyasztása után eggyel nőjön. Amikor a kígyó elfogyaszt egy ennivalót, akkor egy másik jelenjen meg valahol, tehát öt ennivaló mindig legyen a pályán. Ha a kígyó önmagába harap, vagy nekimegy a falnak, akkor a játék véget ér. Ha a kígyó 25 testrész hosszúságú lesz, akkor győzelemmel fejeződjön be a játék.
Beküldendő egy i396.txt állományban a megoldás rövid dokumentációja, amely tartalmazza a megosztott játék internetes elérhetőségét.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
I/S. 6. Adott \(\displaystyle N\) (\(\displaystyle 1\le N\le 1000\)) db tornyunk. Minden toronynak ismerjük a magasságát, ami egész szám 0-tól 100-ig. Akkor tekintjük szépnek a városunkat, ha bármely két torony magasságának különbsége nem nagyobb, mint 17. A város szépítésére építészeket fogadunk. Egy tornyot \(\displaystyle x\) emelettel alacsonyabbra átalakítani, vagy \(\displaystyle x\) emelettel magasabbra építeni \(\displaystyle x^2\) forintba kerül. Adjuk meg, mennyi pénzből tudjuk minimálisan elérni, hogy szép legyen a városunk. Tornyokat csak egész számú emelettel tudunk változtatni. Az átépítés után is teljesülnie kell, hogy minden torony magassága nemnegatív egész.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et, majd a következő \(\displaystyle N\) sorból az egyes épületek magasságát, és írja a standard output első és egyetlen sorába azt a minimális költséget, amellyel a feladat megoldható.
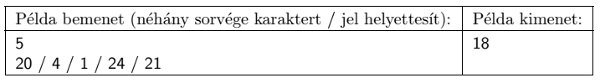
Magyarázat: a 4, 20, 21 magasságú épületeket megtartjuk, az 1-eshez 3-at adunk, a 24-esből 3-at levonunk.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített is6.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
S. 105. Adott egy \(\displaystyle N\times M\) (\(\displaystyle 1\le N, M\le 50\))-es térkép egy szigetvilágról legföljebb 15 szigettel. A térképen a szárazföldet `X', a mély vizet `.' és a sekély vizet `S' jelöli. Béla a téglalap alakú térkép oldalainak megfelelő négy fő irányban tud mozogni. Először ejtőernyővel érkezik egy általa választott szigetre. Egy sziget egy összefüggő szárazföld-darab, azaz olyan X-ek együttese, melyek közt el lehet jutni úgy, hogy közben csak X-re lépünk. Ezután Béla célja az összes sziget végiglátogatása. Béla nagyon jól tud sétálni, ám úszni annál kevésbé. Mély vízben képtelen úszni, így az egyetlen célja, hogy minél kevesebbszer kelljen sekély vízben úsznia. Tehát útja során minél kevesebbszer lépjen S mezőre. Tudjuk, hogy mindenképp meglátogatható az összes sziget.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle M\)-et, majd a következő \(\displaystyle N\) sorból a térképet. Írja a standard output első és egyetlen sorába a lehető legrövidebb összes úszás hosszát a szigetvilág minden szigetének meglátogatása közben.

Magyarázat: A felső szigetről indulva a középsőre 1 úszással, majd a jobb alsóra 2-vel el lehet jutni.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített s105.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

