A KöMaL 2016. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
K. 493. Rá lehet-e írni egy kocka csúcsaira az 1, 2, 3, 4, 5, 6, 7 és 8 számokat úgy, hogy minden lapon prímszám legyen a lap csúcsaiban álló számok összege?
(6 pont)
K. 494. Két háromszög kerülete \(\displaystyle y\) és \(\displaystyle y + 1\) egész számok. Mindkét háromszög egy-egy oldalának hossza \(\displaystyle x\) és \(\displaystyle x + 1\) egész számok. Mekkora a háromszögek harmadik oldala, ha kerületük összege 27?
(6 pont)
K. 495. Egy 30 fős osztályban 12-vel több lány van, mint fiú. Háromfős csapatot akarnak indítani egy versenyen, ahol a csapatban kell lennie legalább egy fiúnak és legalább egy lánynak. Hányféle csapatot tudnak indítani? (Két csapatot akkor tekintünk különbözőnek, ha van legalább egyvalaki, aki az egyik csapatnak tagja, de a másiknak nem.)
(6 pont)
K. 496. Hét jóbarát elhatározza, hogy klubokat alakítanak. Minden klubban hárman lesznek és bármely két klubnak legfeljebb egy közös tagja lehet. Tudnak-e hét klubot alakítani?
(6 pont)
K. 497. Az \(\displaystyle ABC\) derékszögű háromszögben \(\displaystyle BC = 5\), \(\displaystyle AB = 12\). Adjuk meg \(\displaystyle M\) és \(\displaystyle N\) távolságát, ha \(\displaystyle M\)-et az \(\displaystyle A\) középpontú \(\displaystyle AB\) sugarú ív, \(\displaystyle N\)-et a \(\displaystyle C\) középpontú \(\displaystyle BC\) sugarú ív metszette ki az \(\displaystyle AC\) átfogóból.
(6 pont)
K. 498. Egy körvonalat felosztottunk 12 egyenlő részre, majd az osztópontokat összekötöttük az ábrának megfelelően. Határozzuk meg az így keletkezett rombuszok területeinek arányát.
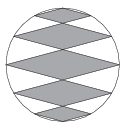
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
C. 1336. Hányféleképpen lehet egy \(\displaystyle 6\times6\)-os négyzetet \(\displaystyle 1\times3\)-as téglalapokra feldarabolni?
(5 pont)
C. 1337. Csongor felesége, Gyopár egy 77 gyönggyel díszített bőrtokot varrt ura születésnapjára. A sikeren felbuzdulva Csongor hagyományőrző dorombegyüttesének minden tagját meglepte egy ugyanilyen tokkal. A tokokat a tagoknak a táltosünnep 50 személyes központi jurtájában adta át nyilvánosan. A kínai boltban százas csomagokban vásárolt gyöngyökből 7 megmaradt, melyekkel Gyopár a hétköznapi pártáját ékesítette. Hányan dorombolnak Csongor zenekarában?
(5 pont)
C. 1338. Legyen az \(\displaystyle ABC\) egyenlőszárú háromszög \(\displaystyle AB\) alapján a \(\displaystyle D\), illetve \(\displaystyle BC\) szárán az \(\displaystyle E\) pont olyan, hogy az \(\displaystyle ACD\), a \(\displaystyle CDE\) és a \(\displaystyle BDE\) háromszögek mind egyenlőszárúak, továbbá a \(\displaystyle BDE\) háromszög hasonló az \(\displaystyle ABC\) háromszöghöz. Mekkorák az egyes háromszögek szögei?
(5 pont)
C. 1339. Egy faiskolában egy \(\displaystyle 30~\rm m\times 40~m\) méretű négyzetrács rácspontjaiba ültettek fákat. A rácsvonalak mentén szomszédos fák távolsága 1 méter. Egy pocok reggeli sétája során úgy járja körbe az ültetvényt, hogy minden pillanatban 1 méterre legyen a hozzá legközelebb eső fától. Mekkora utat tesz meg a pocok, amíg visszaér a kiinduló helyére, ha soha nem fordul vissza?
(5 pont)
C. 1340. Az \(\displaystyle ABCD\) téglalap \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CD\), \(\displaystyle DA\) oldalain rendre felvettük a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), \(\displaystyle S\) pontokat oly módon, hogy a \(\displaystyle PR\) és a \(\displaystyle QS\) szakaszok merőlegesek egymásra. Mutassuk meg, hogy az \(\displaystyle SP\), \(\displaystyle PQ\), \(\displaystyle QR\) és \(\displaystyle RS\) szakaszok felezőpontjai egy téglalapot határoznak meg, és ez a téglalap hasonló az \(\displaystyle ABCD\) téglalaphoz.
(5 pont)
C. 1341. A 2016! legfeljebb hányadik 2-hatvánnyal osztható?
(5 pont)
C. 1342. Adjuk meg az \(\displaystyle a\) paraméter értékét úgy, hogy az alábbi egyenletnek pontosan két megoldása legyen:
\(\displaystyle x^3 -a=\sqrt[3]{x+a}. \)
Adjuk meg a megoldásokat is.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
B. 4768. Határozzuk meg azokat a törteket, melyeknek számlálója és nevezője is kétjegyű szám, a számláló második számjegye pedig megegyezik a nevező első számjegyével, továbbá a tört értéke nem változik, ha a két megegyező számjegyet elhagyjuk.
Javasolta: Velkeyné Gréczi Alice (Ipolyszög)
(3 pont)
B. 4769. Melyek azok a háromszögek, melyek oldalainak harmadolópontjai egy körre illeszkednek?
Szoldatics József (Budapest) javaslata nyomán
(3 pont)
B. 4770. Milyen számjegyre végződhet a pozitív egész \(\displaystyle n\ge 3\) szám, ha \(\displaystyle n+n^{2}+ \ldots+n^{2n-3} - 4\) prímszám?
(4 pont)
B. 4771. Egy százszemélyes repülőgépen száz ember utazik úgy, hogy mindenkinek van előre kiosztott helye. Az első utas ezzel nem törődve véletlenszerűen leül a száz közül egy helyre. Ezután minden utas a saját helyére próbál leülni, vagy ha az foglalt, véletlenszerűen választ egy másikat. Mennyi a valószínűsége annak, hogy a századik utas a helyére ül, ha egyszerre csak egy ember foglal helyet?
Javasolta: Nagy Nándor (Budapest)
(5 pont)
B. 4772. Igaz-e, hogy ha két konvex négyszög négy-négy oldalának és két-két átlójának hossza megegyezik, akkor a két négyszög egybevágó?
Javasolta: Vígh Viktor (Szeged)
(4 pont)
B. 4773. Az \(\displaystyle ABC\) háromszög beírt körének középpontja \(\displaystyle O\), a körülírt köré pedig \(\displaystyle K\). Bizonyítsuk be, hogy az
\(\displaystyle \frac{\overrightarrow{AB}}{AB}+ \frac{\overrightarrow{BC}}{BC}+ \frac{\overrightarrow{CA}}{CA} \)
vektor merőleges az \(\displaystyle OK\) egyenesre.
Javasolta: Holló Gábor (Budapest)
(5 pont)
B. 4774. A \(\displaystyle p_1\) \(\displaystyle \big(y=-x^2+b_1 x+c_1\big)\) és a \(\displaystyle p_2\) \(\displaystyle \big(y=-x^2+b_2 x+c_2\big)\) parabolák érintik a \(\displaystyle p_3\) \(\displaystyle \big(y=x^2+b_3x+c_3\big)\) parabolát. Bizonyítsuk be, hogy az érintési pontokat összekötő egyenes párhuzamos \(\displaystyle p_1\) és \(\displaystyle p_2\) közös érintőjével.
Kvant
(5 pont)
B. 4775. Határozzuk meg azon \(\displaystyle (n,k)\) pozitív egész számpárokat, melyekre tetszőleges \(\displaystyle a_1\ge a_2\ge \ldots \ge a_{2k+1}\ge 0\) valós számok esetén teljesül, hogy
\(\displaystyle \sum_{i=1}^{2k+1} {(-1)}^{i-1} a_{i}^{n}\ge \bigg(\sum_{i=1}^{2k+1} {(-1)}^{i-1} a_{i}\bigg)^{\!\!n}. \)
Javasolta: Somogyi Ákos (Budapest)
(6 pont)
B. 4776. Legyen \(\displaystyle \mathcal{O}\) egy szabályos oktaéder. Hány olyan egyenes van, melyek körüli legfeljebb \(\displaystyle 180^{\circ }\)-os forgatással \(\displaystyle \mathcal{O}\) önmagába vihető?
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2016. március 10-én LEJÁRT. |
A. 662. Az \(\displaystyle A_1\), \(\displaystyle A_2\), \(\displaystyle A_3\), \(\displaystyle A_4\), \(\displaystyle B_1\), \(\displaystyle B_2\), \(\displaystyle B_3\), \(\displaystyle B_4\) pontok, ebben a sorrendben, egy parabolán vannak. Minden \(\displaystyle (i,j)\) pár esetén, amelyre \(\displaystyle 1\le i,j\le4\) és \(\displaystyle i\ne j\), jelölje \(\displaystyle r_{ij}\) azt az arányt, amelyben az \(\displaystyle A_jB_j\) egyenes kettéosztja az \(\displaystyle A_iB_i\) szakaszt. (Ha tehát \(\displaystyle A_iB_i\) és \(\displaystyle A_jB_j\) metszéspontja \(\displaystyle X\), akkor \(\displaystyle r_{ij}=\frac{A_iX}{XB_i}\).) Mutassuk meg, hogy ha az \(\displaystyle r_{12} \cdot r_{21} \cdot r_{34} \cdot r_{43}\), \(\displaystyle r_{13} \cdot r_{31} \cdot r_{24} \cdot r_{42}\) és \(\displaystyle r_{14} \cdot r_{41} \cdot r_{23} \cdot r_{32}\) számok közül közül valamelyik kettő megegyezik, akkor a harmadik is egyenlő velük.
(5 pont)
A. 663. Adott két pozitív egész, \(\displaystyle k\) és \(\displaystyle \ell\). Egy vízszintes és függőleges oldalú négyzetet véges sok téglalapra osztottunk szakaszokkal úgy, hogy a következők teljesülnek:
\(\displaystyle (i)\) a sík bármely vízszintes vagy függőleges egyenese a szakaszok közül legfeljebb egyet tartalmaz;
\(\displaystyle (ii)\) semelyik két szakasz nem keresztezi egymást a belsejükben;
\(\displaystyle (iii)\) minden vízszintes egyenes, amely elmetszi a négyzetet, de nem tartalmazza egyik szakaszt sem, pontosan \(\displaystyle k\) téglalapot metsz el;
\(\displaystyle (iv)\) minden függőleges egyenes, amely elmetszi a négyzetet, de nem tartalmazza egyik szakaszt sem, pontosan \(\displaystyle \ell\) téglalapot metsz el.
Mekkora lehet a téglalapok száma?
Orosz feladat
(5 pont)
A. 664. Legyen \(\displaystyle a_1<a_2<\ldots<a_n\) pozitív egészekből álló számtani sorozat. Mutassuk meg, hogy
\(\displaystyle [a_1,a_2,\ldots,a_n] \ge [1,2,\ldots,n]. \)
(A \(\displaystyle [\ldots]\) szimbólum a legkisebb közös többszöröst jelöli.)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

