A KöMaL 2016. áprilisi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2016. május 10-én LEJÁRT. |
I. 400. Egy \(\displaystyle N\times M\) (\(\displaystyle 10\le N,M\le 10\,000\)) téglalap alakú területen \(\displaystyle K\) (\(\displaystyle 0\le K\le 1\,000\)) darab különböző szélességű és hosszúságú téglalap elszórtan helyezkedik el. A téglalapok oldalai párhuzamosak a terület oldalaival, érintkezhetnek és átfedhetik egymást, de a területről nem nyúlhatnak ki.
Készítsünk programot i400 néven, amely a következő problémákat oldja meg.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et, \(\displaystyle M\)-et és \(\displaystyle K\)-t, majd a következő \(\displaystyle K\) sorból a téglalapok bal felső, illetve jobb alsó sarkainak \(\displaystyle X\) és \(\displaystyle Y\) koordinátáit (egész számok).
A program írja a standard outputra a kérdésekre adott válaszokat soronként:
- soroljuk fel a beolvasás sorrendjében azoknak a téglalapoknak a sorszámát, amelyek a terület határához hozzáérnek;
- adjuk meg, hogy melyik az a téglalap, amelyik a legtöbb más téglalap valamelyik csúcsát tartalmazza; a számításnál az érintkezést ne vegyük figyelembe, több azonos téglalap esetén elegendő egyet megadni;
- adjuk meg, hogy hány olyan téglalap van, amely a többitől független, azaz nem ér egyetlen másik téglalaphoz sem, nem metszi, nem tartalmaz egy másikat sem, illetve őt sem tartalmazzák.
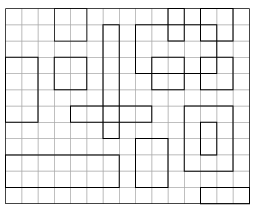
Példa (amelyben az újsor karakterek egy részét a tömörség kedvéért / jellel helyettesítettük):
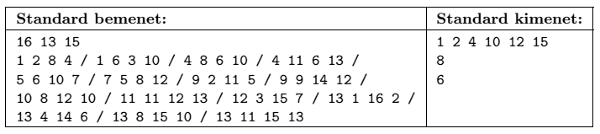
Beküldendő egy tömörített i400.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 401. (É). Az időjárás megfigyelés és előrejelzés mellett a pollenkoncentrációról is jelentést adnak ki a meteorológiai szolgálatok. Ezekben a jelentésekben a veszélyeztetés mértékét a + jelek számával jelzik egy négyfokozatú skálán a legfontosabb allergén növényekre és gomba spórákra. Az allergenitást, az adott növénnyel szembeni tünetek gyakoriságát, a + jelek számával, szintén négy fokozatban közlik.
A honlapunkról letölthető meres.txt fájlban egy kiválasztott hét átlagos pollenterhelésének adatai vannak. A megoldás során törekedjünk képlet, függvény, hivatkozás használatára, a segédszámításokat egy másik munkalapon végezzük, és ne használjunk saját függvényt vagy makrót.
1. Nyissuk meg táblázatkezelő program segítségével a honlapunkról letölthető meres.txt tabulátorokkal tagolt, UTF-8 kódolású adatfájlt úgy, hogy az első érték az A1-es cellába kerüljön. A munkalap nevét Mérés-re változtassuk meg. A munkafüzetet mentsük a táblázatkezelő saját formátumában i401 néven.
2. A táblázat szerkezetét, a cellák formázását változtassuk meg a minta és a leírás szerint.
\(\displaystyle a)\) A munkalapon 7 és 10 pontos betűméretet, valamint Arial betűtípust használjunk.
\(\displaystyle b)\) A cellák igazítását a minta szerint állítsuk be.
\(\displaystyle c)\) Biztosítsuk, hogy az adatokat tartalmazó cellák háttere a veszélyességi kategóriától, azaz a cellákban lévő + jelek számától függjön.

\(\displaystyle d)\) Az adatokat tartalmazó cellák tartományában belül vékony, egyszeres, kívül pedig duplavonalas szegélyt alkalmazzunk.
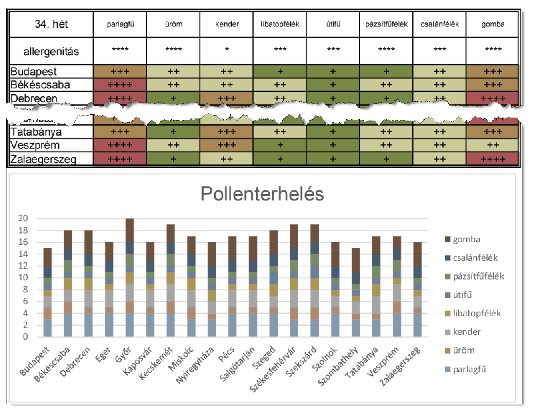
3. Az adatokat tartalmazó cellák alatt halmozott oszlopdiagramon ábrázoljuk városonként a növények heti pollenterhelését. A diagram címét és szerkezetét a minta alapján alakítsuk ki.
4. Hozzunk létre új munkalapot Információ néven a minta szerint. A cellák szövegét, a második sor kivételével, a minta alapján gépeljük be.
5. A harmadik és negyedik cellában határozzuk meg függvények segítségével a második sor első két cellájába írt város és virágnév alapján az allergenitást és a tüneteket a Mérés munkalapon található aktuális értékek alapján.
6. A munkalap formázását a minta szerint végezzük el.
\(\displaystyle a)\) A betűméret és a betűstílus legyen a Mérés munkalapon alkalmazottnak megfelelő.
\(\displaystyle b)\) Ügyeljünk a megfelelő cellák összevonására és az igazításokra.
\(\displaystyle c)\) A második sor első két cellájában világosszürke hátteret, a harmadik és negyedik cellában félkövér betűstílust alkalmazzunk.
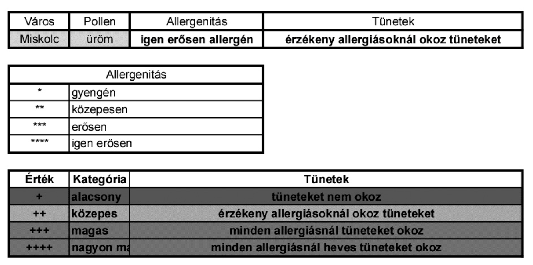
\(\displaystyle d)\) A veszélyességi kategóriák táblázatának cellaháttér színei a Mérés munkalaphoz megadott színeknek feleljenek meg.
Beküldendő egy tömörített i401.zip állományban a megoldást tartalmazó munkafüzet és a megoldás rövid leírását bemutató dokumentáció.
Letölthető fájl: meres.txt
(10 pont)
I. 402. Rendszeresen gyűjtünk adatokat XML fájl formájában. A jólformázott és érvényes XML fájlok előállítását egy példa XML fájllal és egy XML schema fájllal (XSD) segítjük. (Az XML fájl érvényessége az XSD fájl segítségével ellenőrizhető. Az ellenőrzés például a http://www.utilities-online.info/xsdvalidation/ címen is megtehető.)
Ezúttal azonban az XSD fájlt véletlenül töröltük, csak a helyes XML példa áll rendelkezésünkre. Az XSD fájlt programunknak kell előállítania a lehető legpontosabb formában. Az egyes elemekhez a nevet, típust - és ha szükséges –az előfordulás számát kell bejegyezni.
A rendelkezésre álló XML fájlban az adatok legfeljebb négy szinten vannak egymásba ágyazva. (A négy szintbe a gyökérelemet is beleértjük.) Tudjuk, hogy az összetett típusok közül csak a szekvenciális szerepel, az elemi típusok közül pedig a következők fordulhatnak elő: xs:integer, xs:decimal (például 12.34), xs:date (formátuma: éééé-hh-nn, például 2014-01-01), xs:time (formátuma: óó:pp:mm, például 10:30:00). A fel nem ismert típust xs:string-ként adjuk meg. Ha egy elem többször is előfordul, az előfordulások maximális számát végtelenre, ha elmarad, akkor az előfordulások minimális számát pedig nullára állítjuk.
A témában a következő lapokon is tájékozódhatunk, de érdemes továbbiakat is felkutatni:
\(\displaystyle \bullet\) http://www.inf.unideb.hu/~bodai/31-xml_alk/xmlSchemas.html;
\(\displaystyle \bullet\) http://soci.hu/articles/xml/XmlSema.pdf.
A bemeneti fájl egy jólformázott XML fájl. A fájlban a <, >, / karakterek csak a tagekben találhatók meg. A kimeneti fájl egy XSD fájl, amely az első bekezdésben említett címen található űrlapon az XML fájlt érvényesnek mutatja. (A mintafájlok a weblapunkról tölthetők le.)
A program első parancssori argumentuma a bemeneti fájl neve, a második pedig a kimeneti fájl neve legyen.
Beküldendő egy tömörített i402.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
Példa fájlok: zenekar.xml, zenekar.xsd
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2016. május 10-én LEJÁRT. |
I/S. 8. Egy hangya a következő utasítások alapján közlekedik: F (előrelép egyet), L (balra fordul 90 fokot), R (jobbra fordul 90 fokot). A hangyának összesen \(\displaystyle N\) (\(\displaystyle 1\le N\le 100\,000\)) utasítást adunk. A hangya a \(\displaystyle (0;0)\) pontról indul, és azon tűnődik, hogy hányféle végpozícióba juthat el, ha az \(\displaystyle N\) közül pontosan egy utasítást másként csinál. Például L helyett F-et.
A program olvassa be a standard input első sorából az utasításokat tartalmazó szöveget, és írja a standard output első és egyetlen sorába a lehetséges végpozíciók számát.
|
Magyarázat: A két utasítás egyikének megváltoztatásával az FL, FR, RF, LF utasításpárok jöhetnek létre, melyekkel a hangya a \(\displaystyle (0;1)\), \(\displaystyle (0;1)\), \(\displaystyle (1;0)\), és \(\displaystyle (-1;0)\) végpozíciókba kerülhet.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített is8.zip állományban a program, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2016. május 10-én LEJÁRT. |
S. 107. Egy hatalmas négyzethálós terület (\(\displaystyle 10\,000\,000\times 10\,000\,000\)) \(\displaystyle N\) négyzetét (\(\displaystyle 1\le N\le 200\,000\)) egy-egy fa foglalja el. Egy mókus észrevette, hogy bármelyik fáról bármelyikre el tud jutni csak élszomszédos négyzeteken álló fák közötti ugrásokkal. A fákat tartalmazó négyzetek által alkotott összefüggő területben azért lehetnek lyukak, azaz fákat nem tartalmazó négyzetek. Határozzuk meg az erdő külső kerületét, amibe a lyukak nem számítanak bele.
A program olvassa be a standard input első sorából \(\displaystyle N\)-t, majd a következő \(\displaystyle N\) sorból a fák koordinátáit (\(\displaystyle 1\le x, y\le 10\,000\,000\)), és írja a standard output első és egyetlen sorába a kerület nagyságát.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített s107.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

