A KöMaL 2016. májusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2016. június 10-én LEJÁRT. |
I. 403. A csucsok.txt nevű UTF-8 kódolású, szóközökkel tagolt szöveges állomány Magyarország 700 méternél nagyobb hegycsúcsainak nevét, magasságát, a hegység nevét, valamint GPS koordinátáit tartalmazza. Egy hegyhez több hegycsúcs is tartozhat. Az adatfájlban legfeljebb 300 hegycsúcs adata szerepel. Például:
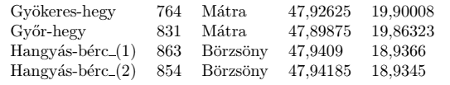
A fenti példában a Hangyás-bérc nevű hegynek két feljegyzett csúcsa is van. Az első 863 m magas, a Börzsönyben található, északi szélessége 47,9409 fok, keleti hosszúsága 18,9366 fok.
Az adatfájlban ékezetes betűk és tizedesvessző szerepelnek. Megengedett lépés az ékezetes betűk lecserélése ékezet nélkülire, továbbá a tizedes vesszők lecserélése tizedes pontra, pl. Jegyzettömbbel vagy más szerkesztővel.
Készítsünk programot i403 néven a következő feladatok megoldására. A program futása során a képernyőre való kiíráskor utaljunk a feladat sorszámára.
1. Olvassuk be a fájlból a csúcsok adatait, és írassuk ki a képernyőre, hogy hány csúcs van az adatfájlban.
2. Kérjük be egy hegy nevének első betűit, és írassuk ki a képernyőre az ennek megfelelő hegycsúcs(ok) adatait. Ha az adott nevű hegy nem szerepel a fájlban, azt is jelezzük. (Például, ha a felhasználó a ,,Hangyá'' szöveget írja be, akkor jelenjen meg minden olyan hegycsúcs, amelynek neve a ,,Hangyá'' szöveggel kezdődik.)
3. Kérjük be egy hegység nevét, és írassuk ki a képernyőre legmagasabb hegycsúcsának nevét és magasságát. Ha az adott hegység nem szerepel az adatfájlban, azt is jelezzük.
4. Listázzuk ki a képernyőre ábécérendben az adatfájlban szereplő hegységek nevét, minden hegységet pontosan egyszer. A hegységek neve mellett jelenjen meg a hegységben lévő, 700 m-nél nagyobb hegycsúcsok száma is!
5. Kérjük be egy hegycsúcs nevét, és határozzuk meg, milyen távol van a Gellért-hegytől, ha a Gellért-hegy északi szélessége \(\displaystyle 47,483 \,736\,2\) fok, keleti hosszúsága \(\displaystyle 19,037\,055\) fok. (Két GPS koordinátákkal meghatározott pont távolságát légvonalban meghatározhatjuk például a Haversine-formulával (https://en.wikipedia.org/wiki/Haversine_formula.) A számításnál a hegycsúcsok magasságkülönbségét ne vegyük figyelembe. A Föld sugara 6371 km.
6. Melyik két hegycsúcs távolsága a legnagyobb? Jelenítsük meg a képernyőn a két hegycsúcs nevét és hegységének nevét, továbbá a távolságukat.
Beküldendő egy tömörített i403.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
Letölthető fájl: csucsok.txt.
(10 pont)
I. 404. A rokonsági fokok ábrázolása nemcsak grafikusan családfával, hanem adatbázis-kezelővel is megoldható. (Erre találhatunk példát a 2006. februári emelt szintű érettségi feladatsorban is.) Ezúttal feladatunkban a Kiss-Nagy család rokonsági viszonyait fogjuk adatbázis-kezelővel elemezni. Az adatbázisban tárolt családfarészletet a következő ábra szemlélteti:
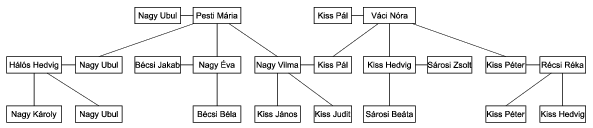
Az adatokat a csaladtagok.txt tabulátorral tagolt, UTF8 kódolású szövegfájl tartalmazza, az első sorban a mezőnevek találhatók.
1. Készítsünk új adatbázist i404 néven. A mellékelt adatállományt importáljuk az adatbázisba csaladtagok néven. Beolvasáskor állítsuk be a megfelelő adatformátumokat és a kulcsot.

Készítsük el a következő feladatok megoldásait. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok viszont ne. A megoldásokat a zárójelben lévő néven mentsük el.
Az adatbázis szerkezete a valódi családi kapcsolatoknak csupán egyszerűsített formája, amely a valós viszonyok leírására nem teljesen alkalmas. Ezért feltételezzük, hogy a családban nem volt válás, újraházasodás, nincsenek féltestvérek. A feladatmegoldás során több esetben is szükségünk lehet arra, hogy az adattáblát több példányban használjuk fel.
2. Adjuk meg lekérdezés segítségével a férfiak és a nők számát. (2ffino)
3. Lekérdezéssel listázzuk ki a házaspárokat. Gondoskodjunk arról, hogy minden házaspár csak egyszer jelenjen meg. (3hazasparok)
4. Kérjük be egy családtag nevét, és adjuk meg anyjának és apjának nevét lekérdezés segítségével. Ha több azonos nevű családtag van, valamennyi adata jelenjen meg. (4apaanya)
5. Listázzuk lekérdezés segítségével a testvéreket. A felsorolásban minden testvérpár pontosan egyszer jelenjen meg. (5testverek)
6. Lekérdezés segítségével határozzuk meg az unokák anyai és apai nagyanyját a mintának megfelelően. Ha a két nagyszülő egyike sem szerepel az adatbázisban, akkor az unoka neve se jelenjen meg. (6nagyi)
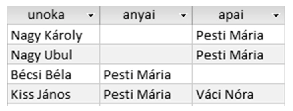
7. Listázzuk ki lekérdezés segítségével az unokatestvéreket. Gondoskodjunk arról, hogy minden pár pontosan egyszer jelenjen meg. (7unokateso)
8. Készítsünk jelentést, amely tartalmazza az adatbázisban szereplő családtagokat névsorban, valamint (ha szerepel az adatbázisban) anyjuk, férjük, feleségük nevét. A megoldást lekérdezés segítségével készítsük elő. A cím és az oszlopfejléc szövege a mintának megfelelően jelenjen meg. (8lista)
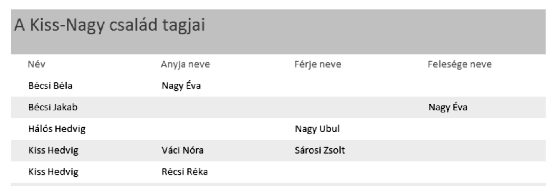
Beküldendő egy tömörített i404.zip állományban az adatbázis, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott adatbázis-kezelő neve, verziószáma.
Letölthető állomány: csaladtagok.txt.
(10 pont)
I. 405. A ,,fogd és vidd'' technika előnyeit több alkalmazásban is használhatjuk. A HTML 5-ös változatában is szerepel, és a legújabb böngészőkben megvalósították. Készítsünk a technika alkalmazásával egy számolást oktató weboldalt draganddrop.html néven, amely alkalmas legföljebb kétjegyű egész számok összeadásának és kivonásának gyakorlására.
Az oldalon betöltésekor, valamint minden helyes megoldás után, jelenjen meg véletlenszerűen néhány egy vagy kétjegyű pozitív vagy negatív szám, valamint az összeadás, a kivonás és az egyenlőségjel. A felhasználónak először össze kell állítania egy feladatot úgy, hogy az oldalon elhelyezkedő elemekből az oldal közepén lévő, szaggatott vonallal jelzett öt téglalapra ráhúzza a megfelelő elemeket. Az első, a harmadik és az ötödik téglalapra a 8 véletlenszerűen kapott számot, a második és negyedik helyre egy műveleti jelet vagy egy egyenlőség jelet lehet ejteni. A program segítségként azonos színnel jelölje a műveleti és relációs jelek téglalapját és helyét. A program ellenőrizze a feladat elkészítését, és ne engedje például, hogy a felhasználó egy nem oda való elemet húzzon egy helyre, vagy egyenlőség nélküli, illetve több egyenlőségjelből álló kifejezést hozzon létre.
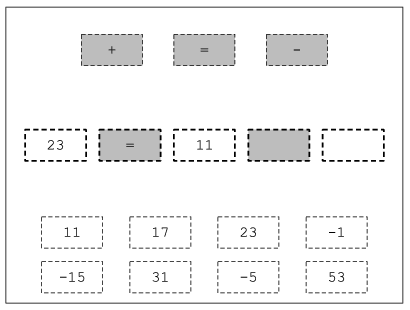
Ha a feladat elkészült, akkor azt jelezze az oldal. Néhány másodperc után a feladathoz nem felhasznált számok és jelek tűnjenek el, és jelenjen meg nyolc darab szám, amelyek között megtalálható az egyenlet megoldása.
A tanulónak most is húzással kell megoldani a feladatot, tehát a szabadon maradt négyzetre kell ejtenie a nyolc szám közül a megfelelőt. A hibás választ ne engedje az oldal, a helyes megoldás jelzése után folytatódjon a gyakorlás a következő feladat létrehozásával.
Az oldalt csak HTML5, CSS és JavaScript elemek segítségével valósítsuk meg. Az oldal ne hivatkozzon, és ne tartalmazzon már kész JavaScript vagy más kiegészítőket.
Beküldendő egy tömörített i405.zip állományban a weboldal teljes forrása, valamint azon böngészők neve és verziószáma, amelyekben az oldal megfelelően működik.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2016. június 10-én LEJÁRT. |
I/S. 9. Blöki \(\displaystyle N\) (\(\displaystyle 1\le N\le 10\)) érdekes pontot lát a síkon, melyeket meg akar látogatni. Blöki csak a koordinátatengelyekkel párhuzamos irányokban tud mozogni, és irányt csak az érdekes pontokon tud változtatni (akár vissza is fordulhat). Blöki dönthet úgy, hogy nem változtat irányt egy érdekes ponton, de úgy akarja az összes pontot meglátogatni, hogy útja során minden érdekes ponton pontosan egyszer változtat irányt: mondjuk azt, hogy ekkor vizsgálja meg az érdekes pontot. Blöki egy érdekes ponton akárhányszor áthaladhat, de pontosan egyszer akarja megvizsgálni. Útja során az összesen érdekes ponton át szeretne haladni, és a kiindulási pontba visszaérni. Blöki azon töpreng, hogy ezekkel a szigorú feltételekkel hányféleképp vizsgálhatja meg az összes pontot. Blöki egy ilyen körútja oda és vissza irányban két különböző útnak számít. Két körút különböző, ha különböző sorrendben vizsgálja Blöki az érdekes pontokat. Készítsünk programot, ami segít Blökinek megszámolni a megfelelő utakat. Blöki bármelyik pontból indulhat, az összes lehetőség érdekli.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et , majd a következő \(\displaystyle N\) sorból az érdekes pontok egész koordinátáit: \(\displaystyle -1000\le x, y\le 1000\). A program írja a standard output első sorába a lehetőségek számát.
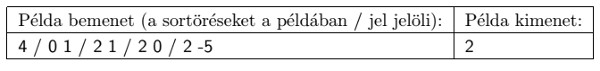
Magyarázat: a két útvonal: 1-2-4-3 és 3-4-2-1, Blöki mindkét esetben az origóból indul.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített is9.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2016. június 10-én LEJÁRT. |
S. 108. András és Béla egy fa-gráfon játszik, melynek \(\displaystyle N\) (\(\displaystyle 1\le N\le 100\,000\)) csúcsa van. Összesen \(\displaystyle M\) (\(\displaystyle 1\le M\le 100\,000\)) lépésből áll a játék. Minden lépés kétféle lehet:
- András kiválasztja a fa két csúcsát, és a köztük lévő egyértelmű út minden élére egy csokit helyez.
- Béla megkérdezi, hogy egy adott élen hány csoki van.
A feladat: Béla kérdéseit gyorsan megválaszolni.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle M\)-et, majd a következő \(\displaystyle N-1\) sorból a fa éleit: \(\displaystyle u\), \(\displaystyle v\) egészeket. Ezután \(\displaystyle M\) sor következik. Minden sor egy P vagy Q betűvel kezdődik, majd egy \(\displaystyle u, v\) egész számpár következik. Ez utóbbi számpár egy csúcspárt jelöl. A ,,P'' betű jelentése, hogy András az \(\displaystyle (u, v)\) csúcsok közti egyértelmű út minden élére tesz egy csokit. A ,,Q'' betű jelentése, hogy Béla megkérdezi, hogy hány csoki van az \(\displaystyle (u, v)\) élen. A program írja a standard output soraiba a Béla kérdéseire adott válaszokat.

Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített s108.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

