A KöMaL 2016. novemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2016. december 12-én LEJÁRT. |
I. 412. Egy társasházban új liftet adnak át, amelynek forgalmát egy adatállományban rögzítik. Ezzel az utazási szokások később elemezhetők. A liftet minden lakó csak a személyes, sorszámozott kártyájával tudja igénybe venni. Az utasok a kártyával történő azonosítás után tudják a liftet az induló szintre hívni és a célnak beírt szintre utazásra használni. Rendelkezésünkre állnak az első hónap napi forgalmi adatai a forgalom.txt állományban.
A napi lifthasználati adatok csoportosítva szerepelnek az adatállományban. Egy-egy naphoz két sor tartozik. Az első sorban a nap sorszáma van, a másodikban az lift igénybevételének adatai szóközzel elválasztva. Egy-egy utazáshoz három adat tartozik: a \(\displaystyle K\) (\(\displaystyle 0\le K\le 15\)) kártyasorszám, az \(\displaystyle I\) induló- és \(\displaystyle C\) célszint (\(\displaystyle 0\le I,C\le 5\)) értéke. A napi utazás számhármasai egy sorban, időrendben szerepelnek egymás után. (Feltételezhetjük, hogy minden utas egyedül utazik, illetve napi 100 utazásnál több nem történik, és legfeljebb 30 nap adatait vizsgáljuk.) Például:
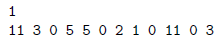
A példában az első napon a 11-es sorszámú kártyával a 3. emeletről a földszintre utaztak, majd az 5. kártyával az 5. emeletről szintén a földszintre.
Készítsünk programot i412 néven, amely a forgalmat leíró állomány adatait felhasználva az alábbi kérdésekre válaszol. A program forráskódját hianyzasok néven mentsük.
A képernyőre írást igénylő részfeladatok eredményének megjelenítése előtt írjuk a képernyőre a feladat sorszámát (például 4. feladat: ). A beolvasás előtt a várt tartalomra vonatkozó üzenetet jelenítsünk meg. Az ékezet nélküli kiírás is megengedett.
1. Olvassuk be a forgalom.txt állomány adatait és a következő feladatokat ezek alapján oldjuk meg.
2. Számoljuk meg, hogy az adatállományban hány lifthasználat adata szerepel.
3. Írjuk ki a képernyőre, hogy hányféle kártyával használták a liftet.
4. Soroljuk fel azokat a kártyasorszámokat külön-külön, amelyekkel csak felfelé, illetve csak lefelé utaztak. Amennyiben nincs ilyen, írjuk ki, hogy ,,Nincs''.
5. Adjuk meg az összes utazási adat figyelembe vételével külön-külön, hogy a lift összesen hány emeletnyi utat tett meg felfelé és lefelé az üresen közlekedéssel együtt. A lift az első nap első utazása előtt a földszinten tartózkodott.
6. Készítsünk függvényt lakhat néven, amely egy paraméterként megadott kártyasorszámhoz megadja, hogy a földszinten kívül, melyik a leggyakoribb cél szint.
7. Legtöbbször a földszintről a lakásuk szintjére utaznak a lakók. Soroljuk fel minden kártyához, hogy a földszinten kívül, melyik a leggyakoribb cél emelet. Ha nem eldönthető a kérdés, akkor írjuk ki ,,Nem eldönthető''.
8. Soroljuk fel azokat a kártyasorszámokat, amelyekkel minden emeletre és a földszintre is utaztak.
9. Kérjünk be egy napot és egy kártyasorszámot, és egy lista.txt nevű szöveges állományba írjuk ki két oszlopban, hogy közvetlenül az utazásai előtt és után milyen kártyasorszámú lakótárs használta a liftet. Ha nem volt ilyen, akkor a megfelelő oszlopba szóköz kerüljön. Például:
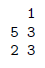
Beküldendő egy tömörített i412.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
Letölthető fájl: forgalom.txt
(10 pont)
I. 413. Ábrázoljunk közös koordináta-rendszerben egy origó középpontú kört és egy azt metsző egyenest, valamint határozzuk meg a metszéspontjaik koordinátáit három tizedesjegy pontossággal táblázatkezelő segítségével.
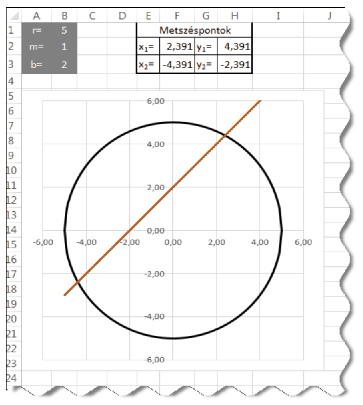
A kör az \(\displaystyle x^{2} + y^{2} = r^{2}\) és az egyenes az \(\displaystyle y = mx + b\) egyenlettel van megadva. Alakítsuk ki a minta szerinti táblázatszerkezetet és a feliratokat készítsük el. A J oszloptól jobbra segédszámításokat végezhetünk, amelyek értelmezését feliratokkal segítsük elő. Állítsuk be, hogy a felhasználó csak a B1:B3 tartomány értékeit módosíthassa, de bármely cella tartalmát megtekinthesse. A hibás adatbevitelt akadályozzuk meg. A megoldásnak csak metsző alakzatokra kell helyes eredményt adnia.
Beküldendő egy tömörített i413.zip állományban a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.
(10 pont)
I. 414. Készítsünk programot a klasszikus Tili-toli játék alábbi, módosított változatára.
Olvassunk be egy képfájlt. Bontsuk fel a képet \(\displaystyle N\times M\) (\(\displaystyle 3\le N\le 5\), \(\displaystyle 3\le M\le 5\)) képkockára (azonos méretű, téglalap alakú részre). Az \(\displaystyle N\) és \(\displaystyle M\) értékét a felhasználó adhatja meg. (A mintán a \(\displaystyle 3\times 4\)-es elrendezést látjuk.)
Keverjük össze a képkockákat, majd az eredetileg jobb alsó sarokban lévőt töröljük. A játék során a felhasználó a képkockákat vízszintesen vagy függőlegesen mozdíthatja el az üres helyre. Akkor nyer, ha minden képkocka az eredeti helyére kerül.

Ügyeljünk arra, hogy keverés után a kép a játék szabályainak betartásával kirakható legyen. Megengedett a képkockákon az eredeti sorrend feltüntetése.
A program készítése során feltételezhetjük, hogy a kép jpg formátumú, a képpontok sorainak és oszlopainak száma 300 és 600 között van. (Mintaként használható a cimlap.jpg, ami a KöMaL egy korábbi borítóját tartalmazza.)
Beküldendő egy tömörített i414.zip állományban a program forráskódja és rövid dokumentációja, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
Letölthető mintaállomány például a legutolsó megjelent szám borítója, melynek címe: http://www.komal.hu/lap/2016-10/cimlap.jpg
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2016. december 12-én LEJÁRT. |
I/S. 12. Adott egy téglalap, melynek oldalai \(\displaystyle a\) és \(\displaystyle b\) hosszúak (\(\displaystyle 1\le a,b\le 10^{9}\) pozitív egész). Fedjük le hézagmentesen és átfedés, valamint kilógás nélkül a téglalapot a lehető legkevesebb számú csempével. Kétféle csempe van: az egyik típusú négyzet alakú, melynek oldalai \(\displaystyle 2^{k}\) hosszúak; a másik típusú téglalap alakú, melynek egyik oldalhossza \(\displaystyle 2^{k}\), másik pedig \(\displaystyle 2^{k+1}\) (\(\displaystyle 0\le k\le N\)).
Készítsünk programot is12 néven, amely kiszámítja, hogy legkevesebb hány csempét kell fölhasználni a lefedéshez. A program olvassa be a standard bemenet első sorából \(\displaystyle a\), \(\displaystyle b\) és \(\displaystyle N\) (\(\displaystyle 0\le N\le 30\)) értékét, majd írja a standard kimenet első sorába a minimálisan szükséges csempék számát.
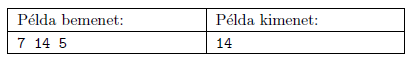
Magyarázat: a \(\displaystyle 7\times 14\)-es téglalap lefedhető egy \(\displaystyle 8\times 4\)-es, egy \(\displaystyle 4\times 4\)-es, négy \(\displaystyle 4\times 2\)-es, egy \(\displaystyle 2\times 2\)-es és hét darab \(\displaystyle 1\times 2\)-es csempével.
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. További 9 pontot ér, ha a program minden helyes bemenetet képes jól megoldani 1 mp futásidőkorláton belül. A programra kapható 9 pontból legföljebb 4 adható azokra a megoldásokra, amelyek csak az \(\displaystyle a, b \le 10^{3}\) nagyságú bemenetekre adnak helyes megoldást az időkorláton belül.
Beküldendő egy tömörített is12.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2016. december 12-én LEJÁRT. |
S. 111. Egy vasútállomáson különböző befogadóképességű személyvagonokból állítanak össze egy szerelvényt. Egy csapat katona az éppen rendezés alatt álló vonatra szeretne felszállni, ezért figyelik, ahogy a vagonokat tologatják. Megfigyelték, hogy a rendező mozdony egyszerre mindig csak egy kocsit mozgat, azaz a fő szerelvény egy helyben áll, és ennek a végére kapcsolhatnak egy vagont, illetve néha meggondolják magukat, ekkor le is kapcsolhatnak egy kocsit a szerelvény végéről vagy az elejéről. Továbbá minden vagonra rá van írva, hogy hány utas fér el benne (egy pozitív egész szám 1 és \(\displaystyle 10^9\) között). Egy tiszt figyeli a vonat összeállítását, és minden mozgatás után szeretné tudni, hogy mekkora osztagokat hozzon létre, ha minden osztag ugyanannyi katonából áll, és úgy kell felszállniuk a vonatra, hogy minden kocsi tele legyen, és az egyes osztagok tagjai ugyanabban a kocsiban utazzanak, továbbá minél kevesebb osztagba szeretné szervezni a katonákat. Mivel az állomáson rengeteg vagon van, ezért lapunk segítségét kérte, hogy ki tudja adni a helyes parancsokat.
A standard bemenet első sorában a mozgatások \(\displaystyle N\) száma van, a következő \(\displaystyle N\) sor mindegyike egy-egy mozgatást ír le:
\(\displaystyle \bullet\) 0 x \(\displaystyle \to\) új vagont kapcsolnak a szerelvény végére, aminek a kapacitása \(\displaystyle x\);
\(\displaystyle \bullet\) 1 \(\displaystyle \to\) lekapcsolják az utolsó vagont;
\(\displaystyle \bullet\) 2 \(\displaystyle \to\) lekapcsolják az első vagont. A standard kimenet \(\displaystyle N\) sort tartalmazzon, minden mozgatás után az osztagok méretét. Amennyiben a szerelvény az egyik mozgatás után üres lenne, akkor sajnos nem lehet létrehozni semekkora csapatokat sem, ezt a 0 szám kiírásával jelezzük. A mozgatások helyesek, vagyis üres szerelvényről sohasem kapcsolnak le kocsit. A szerelvény kezdetben üres.
Pontozás: az első két tesztesetben (2 pont) csak ,,0'' és ,,1'' típusú mozgatások vannak, vagyis a vonat elejét sosem kapcsolják le.
Korlátok: \(\displaystyle 1\le N\le 10^{5}\), időkorlát 1 mp, memórialimit: 256 MB.
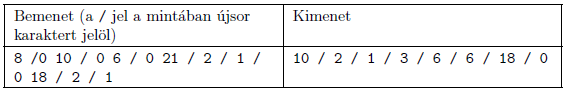
Magyarázat: a szerelvény az egyes műveletek után: (10); \(\displaystyle (10,6)\); \(\displaystyle (10,6,21)\); \(\displaystyle (6,21)\); (6); \(\displaystyle (6,18)\); (18); ().
Pontozás és korlátok: a programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani a fenti korlátoknak megfelelően.
Beküldendő egy tömörített s111.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

