KöMaL Problems in Physics, December 2016
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 10, 2017. |
M. 364. Make a hole in the wall of a cylinder-shaped plastic bottle, and glue a piece of straw horizontally into the hole. Measure the speed of the flowing water as a function of the height of the water.
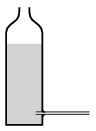
(6 pont)
 |
Problems with sign 'G'Deadline expired on January 10, 2017. |
G. 587. For \(\displaystyle t\) seconds a force \(\displaystyle F\) is exerted on an easily moveable trolley of mass \(\displaystyle m\). The trolley was initially at rest, and after the force ceased the trolley moves freely along the horizontal path. What is the distance covered by the trolley during a time of \(\displaystyle 2t\), measured from the beginning of the motion?
Data: \(\displaystyle m=1.6\) kg, \(\displaystyle F=2\) N, \(\displaystyle t=0.5\) s.
(3 pont)
solution (in Hungarian), statistics
G. 588. The same amount of water is poured into five alike glasses. One ball as well was placed into each glass. The radius of each ball is either 1 cm, 2 cm or 3.5 cm. Then the weight of each glass with the water and the ball in it was measured, and according to their weights they were placed into an increasing order. What is this order and why?
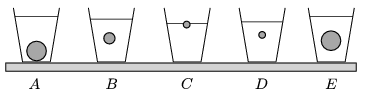
(3 pont)
solution (in Hungarian), statistics
G. 589. If an object were projected on the Moon first at an angle of elevation of \(\displaystyle 60^\circ\) and then at an angle of elevation of \(\displaystyle 30^\circ\), by what factor would the height and the time of flight be greater in the first case than those of in the second case?
(3 pont)
 |
Problems with sign 'P'Deadline expired on January 10, 2017. |
P. 4884. A small steel ball having a diameter of a few centimetres and a big beach ball are projected upward at the same speed of a few m/s. Sketch the velocity-time graphs of both balls in the same coordinate system.
Compare the initial and the final velocities of the balls. Is there any moment when the slopes of the two curves are the same? Which object goes higher and how can this be seen in the graphs?
(4 pont)
solution (in Hungarian), statistics
P. 4885. Two boxes are placed onto each other as shown in the figure, and then they are released from the top of a slope of angle of elevation of \(\displaystyle \alpha\). The coefficient of static friction between the two boxes (of uniform density) is large enough so the two boxes do not slip on each other, but the two boxes slide together on the slope of coefficient of kinetic friction of \(\displaystyle \mu\).
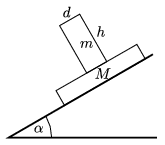
What is the condition for the box on the top not to be toppled over?
(5 pont)
solution (in Hungarian), statistics
P. 4886. The relative humidity of the air in a container of constant volume of \(\displaystyle 10~\rm m^3\) is 50%. The air cools down from a temperature of \(\displaystyle 30~{}^\circ\)C to \(\displaystyle 5~{}^\circ\)C. How much water precipitates out?
(4 pont)
solution (in Hungarian), statistics
P. 4887. There is a plane mirror opposite to a concave mirror of focal length of \(\displaystyle f\). The plane mirror is perpendicular to the principal axis of the concave mirror and the two mirrors are at a distance of \(\displaystyle d\) from each other (measured along the principal axis). Where should a point-like light source \(\displaystyle T\) be placed in order that the light rays emerging from it and reflected in the concave mirror and then in the plane mirror form an image at the position of the light source, and also the rays which are reflected in the plane mirror and then in the concave mirror form an image at the same point? Under what conditions can this happen?
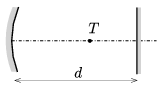
(4 pont)
solution (in Hungarian), statistics
P. 4888. The area of the plates of a parallel plate capacitor is 2 dm\(\displaystyle {}^2\), and their distance is 1 cm. The condenser is charged to a potential difference of 1000 V and then it is disconnected from the voltage source.
\(\displaystyle a)\) What is the surface density of the charge on the plates?
\(\displaystyle b)\) What is the magnitude of the force between the plates?
\(\displaystyle c)\) By what amount does the energy of the capacitor increase if the plates are displaced to a distance of 1.5 cm?
(4 pont)
solution (in Hungarian), statistics
P. 4889. A regular icosahedron is made of wires of the same length and of the same resistance of \(\displaystyle R\).
\(\displaystyle a)\) What is the equivalent resistance between two vertices which are opposite to each other?
\(\displaystyle b)\) What is the dissipated power at each resistor when a voltage of \(\displaystyle U\) is applied across these two opposite vertices?
(4 pont)
solution (in Hungarian), statistics
P. 4890. A point-like object of mass \(\displaystyle m=1\) g and of charge \(\displaystyle Q=2\cdot 10^{-7}\) C is in uniform vertically upward electric field of magnitude \(\displaystyle E=6\cdot 10^4\) V/m. The object is given an initial downward speed of \(\displaystyle v_0=2\) m/s at an angle of \(\displaystyle \varphi=30^\circ\) with respect to the vertical.
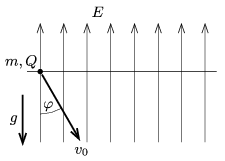
\(\displaystyle a)\) To what maximum depth measured from the level of projection does it go down?
\(\displaystyle b)\) How much time elapses until it reaches the lowest position?
\(\displaystyle c)\) What will its distance from its starting point be \(\displaystyle t=1.8\) s after it was started?
(5 pont)
solution (in Hungarian), statistics
P. 4891. Uniform electric and magnetic fields are generated in vacuum: \(\displaystyle E=7\cdot 10^6\) N/C, \(\displaystyle B=0.02~\rm Vs/m^2\). Is it possible that an electron undergoes uniform straight line motion in some direction?
(4 pont)
solution (in Hungarian), statistics
P. 4892. Is it possible that in the line spectrum of an element the sum of two existing frequencies is also an existing frequency of the same element?
(3 pont)
solution (in Hungarian), statistics
P. 4893. Bodies of different masses and different velocities are colliding with objects of mass \(\displaystyle M\), which are at rest. The collisions are head-on, totally elastic and the speed of each body is much less than the speed of light.
\(\displaystyle a)\) Determine the energy \(\displaystyle W\) given to the initially stationary object, in terms of the energy \(\displaystyle E\), and linear momentum \(\displaystyle I\) of the object which collides with it.
\(\displaystyle b)\) Sketch the graph of the function \(\displaystyle W(E,I)\) for fixed linear momentum \(\displaystyle I_0\), then for fixed energy \(\displaystyle E_0\).
\(\displaystyle c)\) Is it possible that an object having less energy gives more energy to the initially stationary body another one having more energy?
(6 pont)
Upload your solutions above.
