A KöMaL 2017. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2017. február 10-én LEJÁRT. |
M. 365. Méréssel határozzuk meg azt a vízmélységet, ahonnan elengedve egy pingponglabdát az
\(\displaystyle a)\) teljes egészében kibukik a vízből;
\(\displaystyle b)\) a lehető legmagasabbra emelkedik a víz felszíne fölé!
Zsigri Ferenc, Budapest
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2017. február 10-én LEJÁRT. |
G. 590. A repülőgépek kondenzcsíkja nem közvetlenül a gépnél, hanem attól bizonyos távolságra kezdődik, és úgy követi a repülőgépet, mintha az egy kötélen húzná maga után a csíkot. Vajon miért van ez így?
Kérdezi: Zétényi Áron, Budapest, Fodros Általános Iskola
(3 pont)
G. 591. Egy repülőgép ,,szembeszélben'' 8 óra alatt tud \(\displaystyle A\)-ból \(\displaystyle B\)-be repülni, visszafelé ,,hátszélben'' 7 óra alatt ér \(\displaystyle B\)-ből \(\displaystyle A\)-ba. A mindvégig állandónak tekintett szélsebességnek hányszorosa a repülőgép sebessége szélcsendben?
(3 pont)
G. 592. \(\displaystyle H\) magasságból elejtett labda \(\displaystyle h<H\) magasságban a vízszintessel \(\displaystyle 45^\circ\)-os szöget bezáró ferde fallal ütközik, amelyről tökéletesen rugalmasan visszapattan.
\(\displaystyle a)\) Mekkora \(\displaystyle h\) magasságból pattan a labda (vízszintes irányban mérve) a legmesszebbre?
\(\displaystyle b)\) Mekkora ez a maximális távolság?
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2017. február 10-én LEJÁRT. |
P. 4894. Foucault (ejtsd: fukó) francia fizikus 1851-ben a párizsi Pantheonban 67 m hosszú, 28 kg tömegű ingával végezte a Föld forgását kimutató híres kísérletét.
\(\displaystyle a)\) Miért volt szükség ilyen hosszú ingára és ilyen nehéz ingatestre?
\(\displaystyle b)\) Mennyi volt az inga lengésideje?
Közli: Groma István, Budapest
(4 pont)
P. 4895. Egy \(\displaystyle \ell\) hosszúságú, \(\displaystyle M\) tömegű és egy \(\displaystyle 2\ell\) hosszúságú, \(\displaystyle 2M\) tömegű homogén rúd az ábra szerinti helyzetben található. Milyen irányú és mekkora gravitációs erő hat az \(\displaystyle m\) tömegű pontszerű testre? (Keressünk elemi megoldást!)
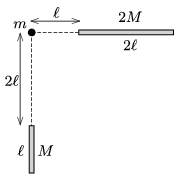
Közli: Kobzos Ferenc, Dunaújváros
(5 pont)
P. 4896. Egy kicsi sportrepülőgép ,,szembeszélben'' 3 óra alatt tud \(\displaystyle A\)-ból pontosan észak felé \(\displaystyle B\)-be repülni, visszafelé ,,hátszélben'' 2 óra alatt ér \(\displaystyle B\)-ből \(\displaystyle A\)-ba. Mennyi idő alatt tenné meg az utat oda-vissza, ha állandóan északkeleti szél fújna? (A szél sebessége mindvégig ugyanakkorának tekinthető.)
Közli: Gnädig Péter, Vácduka
(4 pont)
P. 4897. Függőlegesen álló, felül nyitott, henger alakú edényből az alul lévő csapon keresztül folyik ki a víz. Hogyan változik a víz felszínének süllyedési sebessége? Ha \(\displaystyle T\) idő alatt folyik ki a víz fele az edényből, mennyi idő alatt ürül ki teljesen az edény?
Példatári feladat nyomán
(5 pont)
P. 4898. Az ábrán látható U-alakú cső szárai függőlegesek. A jobb oldali szára zárt, a bal oldalit mozgatható dugattyú zárja le. Kezdetben a csőben azonos magasságig higany van, felette mindkét oldalon \(\displaystyle h\) magasságú, légköri nyomású levegőoszlop helyezkedik el. Mennyit mozdulnak el a higanyszintek, ha a dugattyút lassan \(\displaystyle h/2\) hosszúsággal lejjebb toljuk?
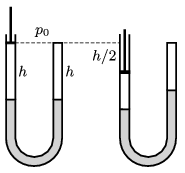
Adatok: \(\displaystyle h=30\) cm, és a légköri nyomás \(\displaystyle H\eg 76\) cm magas higanyoszlop nyomásával egyezik meg.
Közli: Légrádi Imre, Sopron
(4 pont)
P. 4899. Nagy kiterjedésű, homogén elektromos mező erővonalai vízszintesek. A térerősség nagysága \(\displaystyle E=10^4\) N/C. Ennek a mezőnek egy pontjából \(\displaystyle v_0=2\) m/s függőleges sebességgel feldobunk egy \(\displaystyle m=4\) g tömegű fémgolyót, amelynek előzetesen \(\displaystyle q=3\cdot10^{-6}\) C pozitív töltést adtunk.
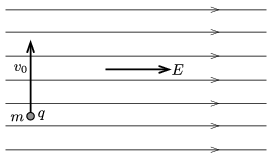
\(\displaystyle a)\) Mekkora elmozdulás után lesz a sebességének nagysága a kezdősebességével egyenlő?
\(\displaystyle b)\) Mennyi idő telik el eddig?
\(\displaystyle c)\) Mozgása során mekkora a legkisebb sebessége?
\(\displaystyle d)\) Hol mozog a leglassabban?
Közli: Holics László, Budapest
(4 pont)
P. 4900. Érdekes optikai játék két egymással szembefordított, azonos görbületi sugarú, homorú gömbtükör, melyek közül a felső tükör közepén egy néhány centiméter átmérőjű, kör alakú lyuk van. A tükrök olyan távolságra vannak egymástól, hogy az alsó tükör közepére tett kicsiny tárgy (például egy szem cukor) képe a lyukas tükör közepén jelenik meg, miután a tárgyról induló fénynyaláb előbb a felső, azután az alsó tükörről is egyszer visszaverődött.
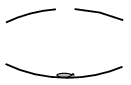
\(\displaystyle a)\) Milyen messze lehet egymástól a két tükör közepe?
\(\displaystyle b)\) Egyenes vagy fordított állású, valódi vagy látszólagos a megjelenő kép, és mekkora a nagyítás?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4901. Joseph Fraunhofer német optikus 1814-ben kezdődő méréseiben 570 sötét vonalat talált a Nap színképében, és azokat betűkkel (esetenként számindexes betűkkel) jelölte. Egy bizonyos optikai rácsban 500 rés esik 1 mm-re. Az egyik Fraunhofer-féle színképvonal két képét (a nulladrendű maximumra szimmetrikusan) egymástól 196,6 cm-re látjuk a rácstól 3,6 m távol lévő ernyőn.
Mekkora ezen színképvonal hullámhossza, és melyik Fraunhofer-vonalról lehet szó?
Régi (1933-as) tankönyvi feladat nyomán
(4 pont)
P. 4902. Egy kezdetben semleges, 5 cm sugarú, szigetelőnyélen lévő, tömör vörösréz golyót 5 kV-os feszültségforrás negatív kivezetésével feltöltöttünk. (A pozitív kivezetést leföldeltük.) Hány százalékkal növekedett a rézgolyó elektronjainak száma?
Közli: Vass Miklós, Budapest
(4 pont)
P. 4903. Felül rögzített, \(\displaystyle L\) hosszúságú, elhanyagolható tömegű, szigetelő anyagból készített fonál alsó végére egy kis méretű, \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű golyót rögzítünk. A fonál és a golyó alkotta rendszer homogén mágneses mezőben van, \(\displaystyle \boldsymbol B\) az ábra síkjára merőlegesen befelé mutat.
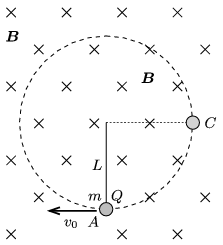
A golyót a fonálra és a mágneses indukcióvektorra merőlegesen elindítjuk. Megfelelő kezdősebesség esetén a golyó úgy halad végig a körpályáján, hogy a fonál mindvégig feszes marad.
\(\displaystyle a)\) Mekkora a \(\displaystyle B\) mágneses indukció értéke, ha az ilyen mozgáshoz szükséges legkisebb kezdősebesség \(\displaystyle v_0=\frac 12 \sqrt{17Lg}\,\)?
\(\displaystyle b)\) Ilyen kezdősebesség mellett hányszor nagyobb a fonalat feszítő erő az \(\displaystyle A\) pontban, mint amikor a test a \(\displaystyle C\) pontban van?
Közli: Kotek László, Pécs
(5 pont)
P. 4904. Az ábrán látható kapcsolásban a \(\displaystyle C\) kapacitású kondenzátor feszültsége kezdetben \(\displaystyle 2U_0\), a \(\displaystyle 2C\) kapacitású kondenzátor töltetlen.
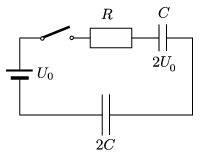
Mennyi hő fejlődik az \(\displaystyle R\) ellenálláson, miután zártuk a kapcsolót?
Közli: Szász Krisztián, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

