KöMaL Problems in Physics, February 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on March 10, 2017. |
M. 366. Prepare a water manometer (with one side open) from a piece of bent plastic tube. Measure the gauge pressure of the air in differently inflated (approximately spherical) balloons. How does this gauge pressure depend on the diameter of the balloon?
(6 pont)
 |
Problems with sign 'G'Deadline expired on March 10, 2017. |
G. 593. The driver of a car travelling at a speed of 18 km/h catches the sight of a van, 250 m ahead of the car, travelling at a constant speed of 54 km/h. Then the car starts to accelerate at a constant rate, and it reaches the van in 20 seconds.
\(\displaystyle a)\) What is the acceleration of the car?
\(\displaystyle b)\) By what distance does the car overtake the van during the next 20 seconds, if it stops accelerating at the moment when it reaches the van?
(3 pont)
solution (in Hungarian), statistics
G. 594. An elastic rubber rope hangs from the ceiling of the gymnasium. Little Bert hangs on the rope and swings vertically at a period of 5 seconds.
What should he do in order to decrease the period to 3 seconds?
(3 pont)
solution (in Hungarian), statistics
G. 595. The mass of the load hanging on a wire rope, attached to the crab of a bridge crane (hoist trolley) is 500 kg. The trolley is moving horizontally at an acceleration of \(\displaystyle 0.1~{\rm m/s}^2\).
What is the (constant) angle enclosed by the wire rope and the vertical?
(3 pont)
 |
Problems with sign 'P'Deadline expired on March 10, 2017. |
P. 4905. A one-metre-long vertical glass tube with one side open end closed the other is pushed into some liquid, such that its open end is at its bottom. The closed end of the tube is held at the level of the surface of the liquid. It is observed that the liquid fills a 7.7 cm-long part of the tube. The ambient air pressure is 100 kPa.
What is the density of the liquid?
(3 pont)
solution (in Hungarian), statistics
P. 4906. What is the temperature of a sample of oxygen gas if the average speed of the molecules is the same as the average speed of the particles in a sample of helium gas at a temperature of \(\displaystyle 0~{}^\circ\)C?
(3 pont)
solution (in Hungarian), statistics
P. 4907. At what \(\displaystyle V_x\) volume will the efficiency of the two heat engines, operated with constant-mass ideal gas as working substance, be the same if they are taken through the cyclic processes A and B shown in the figure?
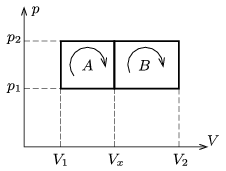
(4 pont)
solution (in Hungarian), statistics
P. 4908. A point-like mass \(\displaystyle m\) is attached to one end of a negligible-mass rod of length \(\displaystyle \ell\). The other end is fixed to a hinge about which the system can be rotated. At which angle \(\displaystyle \alpha\) will the centripetal acceleration of the object at the end of the rod be the same as the tangential component of the acceleration of the object if the system was released from the vertical, unstable position of the rod?
Does the object pull or push the rod at this instant? (Neglect friction.)
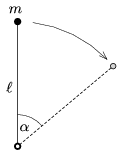
(4 pont)
solution (in Hungarian), statistics
P. 4909. Six tubes are attached to the rim of a wheel, which can rotate about a horizontal axis, as shown in the figure. In each tube there is a heavy lead ball. On the right-hand side the balls are at that end of each tube which is further away from the axle, and on the left-hand side the balls are at the closer ends of the tubes. Explain why this machinery cannot operate forever (cannot be a perpetuum mobile)?
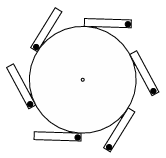
(5 pont)
solution (in Hungarian), statistics
P. 4910. We would like to go from point \(\displaystyle B\) to point \(\displaystyle A\), which points are both in a forest. In any direction among the trees we can walk at a speed of \(\displaystyle u\). There is however exactly one straight road through the forest along which it is easy to go, at a speed of \(\displaystyle ku\), \(\displaystyle k>1\). Point \(\displaystyle A\) is on this road, but point \(\displaystyle B\) is not, and the angle between the road and the line segment \(\displaystyle AB\) is \(\displaystyle \alpha\). How should we walk in order to reach point \(\displaystyle A\) from \(\displaystyle B\) in the shortest time?
(5 pont)
solution (in Hungarian), statistics
P. 4911. Calculate the moment of inertia of a homogeneous triangle-shaped sheet with sides \(\displaystyle a\), \(\displaystyle b\), and \(\displaystyle c\), and of mass \(\displaystyle m\) around a rotational axis, which is perpendicular to the plane of the triangle and goes through the centroid of the triangle. (The problem can be solved in an elementary way as well.)
(5 pont)
solution (in Hungarian), statistics
P. 4912. One end of a flexible, heavy rope of length \(\displaystyle L\) is attached to the ceiling, whilst the other end hangs freely. Below the suspension the rope is hit horizontally. How long does it take for the transverse signal (shock wave), generated near the suspension point, to reach the bottom end of the rope?
(5 pont)
solution (in Hungarian), statistics
P. 4913. A small ball of mass \(\displaystyle m=0.3~\)g and of charge \(\displaystyle Q=2\cdot 10^{-7}\) C is attached to a thin, negligible-mass thread of length \(\displaystyle \ell=20\) cm. The thread with the ball is displaced horizontally, and released without initial speed.
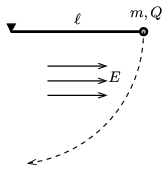
\(\displaystyle a)\) What is the greatest speed of the ball if the whole pendulum is in a uniform horizontal electric field of \(\displaystyle E=10^4\) N/C?
\(\displaystyle b)\) What is the angle between the thread and the vertical when the pendulum is in its other extreme position?
(Air drag is negligible.)
(4 pont)
solution (in Hungarian), statistics
P. 4914. In a series \(\displaystyle RL\) circuit \(\displaystyle (a)\) the phase difference between the voltage and the current is \(\displaystyle 45^\circ\). This phase difference is \(\displaystyle 65^\circ\) and \(\displaystyle 70^\circ\), when another inductor of inductance \(\displaystyle L\) (same as the inductance of the coil in the circuit) is connected in series into the circuit, once next to the resistor as shown in figure \(\displaystyle (b)\) and then next to the original inductor as shown in figure \(\displaystyle (c)\), respectively. How can this happen?
What is the ratio of the impedances in the three cases?

(5 pont)
solution (in Hungarian), statistics
P. 4915. One of the research space ships of the titanium-devouring little green people found a spherical-shaped small asteroid, which has no atmosphere and does not rotate. The scientists bored a tunnel through the planet along one of its diameter, and found that the whole planet consists of titanium of uniform density.
They celebrated the opening of the tunnel with fireworks. By means of a cannon a projectile was shot exactly vertically downward through the tunnel such that the projectile emerged at the other end of the tunnel, and rose to a height which was same as the diameter of the asteroid measured from the surface of the asteroid, and there it exploded spectacularly. The experts of the Examining Institute for Cosmic Accidents (EXINCA) timed the explosion such that it occurred exactly at a time of \(\displaystyle T\) elapsed after shooting the projectile.
Find (both the formula and the numerical value of) this elapsed time of \(\displaystyle T\).
(6 pont)
Upload your solutions above.
