KöMaL Problems in Mathematics, February 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on March 10, 2017. |
K. 535. Is it possible to arrange the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10 in the star pentagon in the figure, so that the sum of the numbers is the same along each line of four points?
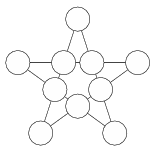
(6 pont)
solution (in Hungarian), statistics
K. 536. For the angles of the star pentagon in the figure, determine the value of \(\displaystyle \alpha + \beta + \gamma +\delta + \varepsilon\).
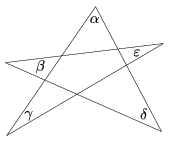
(6 pont)
solution (in Hungarian), statistics
K. 537. How many multiples does 9 have that consist of even digits, all different?
(6 pont)
solution (in Hungarian), statistics
K. 538. The number 2592 may be called ``printer safe'' because it does not cause any error to print the product \(\displaystyle 2^5\, 9^{2}\) as 2592, since the product is equal to this number. Find out in what way the number 13942125 may be considered ``printer safe'', that is, which digits could be interpreted as exponents without changing the value of the result.
(6 pont)
solution (in Hungarian), statistics
K. 539. In how many different ways is it possible to write the numbers 1, 2, 3, 4, 5, 6, 7 and 8 on the vertices of a cube, so that the sum of the four numbers is the same around each face of the cube? (Two solutions are considered the same if each number has the same neighbours adjacent to it.)
(6 pont)
solution (in Hungarian), statistics
K. 540. On the planet XL, there are 180 days in a year, and 10 days in a month. Every seventh year is made an XL year, which means adding an extra day to the third month, making it 11 days long. The week consists of 5 days, called AX, EX, IX, OX and UX, in this order.
Pax was born on the first day of the fourth month of an XL year. Today, on an OX day, he is exactly 25 years old. His son, Felix is 2 years, 3 months and 5 days old today. When Felix is exactly half as many days old as his father, he will have his coming of age ceremony. On what day of the week will the ceremony be held?
(Proposed by L. Lorántfy, Dabas)
(6 pont)
 |
Problems with sign 'C'Deadline expired on March 10, 2017. |
C. 1399. In a 50-metre running race, if Martin gives a 4-metre advantage to Bill, he will just catch up with him at the finish line. If Bill gives 15 metres of advantage to Henry in a 200-metre race, they will finish side by side. How many metres of advantage may Martin give to Henry in a 1000-metre race so that the two of them finish together? (Assume that each of the three runners maintains the same constant running speed throughout the races.)
(5 pont)
solution (in Hungarian), statistics
C. 1400. Prove that if the interior angles of a convex hexagon are equal then the difference of each pair of opposite sides is the same.
(5 pont)
solution (in Hungarian), statistics
C. 1401. The positive numbers \(\displaystyle x\), \(\displaystyle y\) satisfy the equation \(\displaystyle x^3+y^3=x-y\). Prove that \(\displaystyle x^2+y^2<1\).
(5 pont)
solution (in Hungarian), statistics
C. 1402. On each side of a square, either a regular triangle or a square of the same side length is drawn, on the outside. Altogether, there are two triangles and two new squares drawn. What is the radius of the smallest possible circle that completely covers the complex figure obtained in this way?
(5 pont)
solution (in Hungarian), statistics
C. 1403. An \(\displaystyle n\)-element set has half as many \(\displaystyle {(k-1)}\) element subsets as \(\displaystyle k\)-element subsets, and \(\displaystyle \frac 74\) times as many \(\displaystyle {(k + 1)}\) element subsets as \(\displaystyle k\)-element subsets. Determine the number of \(\displaystyle k\)-element subsets of the set.
(Proposed by L. Koncz, Budapest)
(5 pont)
solution (in Hungarian), statistics
C. 1404. \(\displaystyle D\) is the foot of the perpendicular drawn to side \(\displaystyle BC\) of an isosceles triangle \(\displaystyle ABC\) from the midpoint \(\displaystyle F\) of base \(\displaystyle AB\). The midpoint of line segment \(\displaystyle FD\) is \(\displaystyle G\). Prove that \(\displaystyle AD\) is perpendicular to \(\displaystyle CG\).
(5 pont)
solution (in Hungarian), statistics
C. 1405. There are 10 balls in a bag, 6 of which are red. We play the following game: four balls are drawn at random. If \(\displaystyle k\) of them are red, we get \(\displaystyle k^2\) forints (HUF Hungarian currency). What is the expected value of the money gained if one game costs 1 forint?
(5 pont)
 |
Problems with sign 'B'Deadline expired on March 10, 2017. |
B. 4849. The centre of the inscribed circle of \(\displaystyle ABC\triangle\) is \(\displaystyle K\), and the centre of the excircle drawn to side \(\displaystyle AB\) is \(\displaystyle L\). Prove that the line segment \(\displaystyle KL\) and the arc \(\displaystyle AB\) of the circumscribed circle not containing \(\displaystyle C\) bisect each other.
(3 pont)
solution (in Hungarian), statistics
B. 4850. Solve the following simultaneous equations in the set of real numbers:
\(\displaystyle \sqrt{x_1}+\sqrt{x_2}+\ldots+\sqrt{x_{2016}} =\sqrt{2017}\,,\)
\(\displaystyle x_1+x_2+\ldots+x_{2016} =2017.\)
(Proposed by J. Szoldatics, Budapest)
(3 pont)
solution (in Hungarian), statistics
B. 4851. Prove that if all three roots of the equation
\(\displaystyle x^3-px^2+qx-r=0 \)
are positive then the sum of the reciprocals of the roots is at most \(\displaystyle \frac{p^2}{3r}\).
(Proposed by M. Kovács, Budapest)
(4 pont)
solution (in Hungarian), statistics
B. 4852. Triangle \(\displaystyle A_1B_1C_1\) is inscribed in triangle \(\displaystyle ABC\), and triangle \(\displaystyle A_2B_2C_2\) is circumscribed about it as shown in the figure, where \(\displaystyle A_1B_1\parallel A_2B_2\), \(\displaystyle B_1C_1\parallel B_2C_2\) and \(\displaystyle C_1A_1\parallel C_2A_2\). The areas of triangles \(\displaystyle ABC\), \(\displaystyle A_1B_1C_1\) and \(\displaystyle A_2B_2C_2\) are \(\displaystyle t\), \(\displaystyle t_1\) and \(\displaystyle t_2\), respectively.
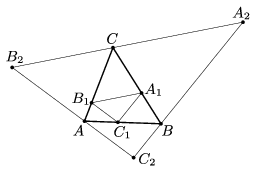
Prove that \(\displaystyle t^2=t_1\cdot t_2\).
(Proposed by S. Róka, Nyíregyháza)
(5 pont)
solution (in Hungarian), statistics
B. 4853. Let \(\displaystyle K\) denote the centre of the incircle of a circumscribed quadrilateral \(\displaystyle ABCD\). \(\displaystyle M\) is a point on the line segment \(\displaystyle AK\), and \(\displaystyle N\) is a point on the line segment \(\displaystyle CK\), such that \(\displaystyle 2 MBN\sphericalangle= ABC\sphericalangle\). Prove that \(\displaystyle 2 MDN\sphericalangle=ADC\sphericalangle\).
(5 pont)
solution (in Hungarian), statistics
B. 4854. Let \(\displaystyle a_1,a_2,\dots,a_n\) be real numbers. Consider the \(\displaystyle 2^n-1\) (nonempty) sums composed out of these numbers. How many of these may be positive?
(5 pont)
solution (in Hungarian), statistics
B. 4855. A table is filled in with digits of 0 and 1 such that there are no two identical rows, but there are two identical rows in any \(\displaystyle 4\times 2\) sub-table formed by two columns and four rows. Show that there exists a column in which one kind of digit occurs exactly once.
(Proposed by Á. Lelkes)
(6 pont)
solution (in Hungarian), statistics
B. 4856. Point \(\displaystyle P\) is said to be a centre of convexity of a point set \(\displaystyle \mathcal{H}\) if \(\displaystyle \mathcal{H}\cup H_P'\) is convex, where \(\displaystyle H_P'\) is the reflection of the point set \(\displaystyle \mathcal{H}\) in the point \(\displaystyle P\). Show that
\(\displaystyle a)\) every convex quadrilateral of the plane has three distinct non-collinear centres of convexity;
\(\displaystyle b)\) a tetrahedron has no centre of convexity.
(6 pont)
solution (in Hungarian), statistics
B. 4857. Determine all pairs \(\displaystyle (n,k)\) of positive integers for which \(\displaystyle \big(2^{2^n}+1\big)\big(2^{2^k}+1\big)\) is divisible by \(\displaystyle nk\).
(Bulgarian problem)
(6 pont)
 |
Problems with sign 'A'Deadline expired on March 10, 2017. |
A. 689. Let \(\displaystyle f_1,f_2,\ldots\) be an infinite sequence of continuous \(\displaystyle \mathbb{R}\to\mathbb{R}\) functions such that for arbitrary positive integer \(\displaystyle k\) and arbitrary real numbers \(\displaystyle r>0\) and \(\displaystyle c\) there exists a number \(\displaystyle x\in(-r,r)\) with \(\displaystyle f_k(x)\ne cx\). Show that there exists a sequence \(\displaystyle a_1,a_2,\ldots\) of real numbers such that \(\displaystyle \sum_{n=1}^\infty a_n\) is convergent, but \(\displaystyle \sum_{n=1}^\infty f_k(a_n)\) is divergent for every positive integer \(\displaystyle k\).
(5 pont)
A. 690. In a convex quadrilateral \(\displaystyle ABCD\), the perpendicular drawn from \(\displaystyle A\) to line \(\displaystyle BC\) meets the lines \(\displaystyle BC\) and \(\displaystyle BD\) at \(\displaystyle P\) and \(\displaystyle U\), respectively. The perpendicular drawn from \(\displaystyle A\) to line \(\displaystyle CD\) meets the lines \(\displaystyle CD\) and \(\displaystyle BD\) at \(\displaystyle Q\) and \(\displaystyle V\), respectively. The midpoints of the segments \(\displaystyle BU\) and \(\displaystyle DV\) are \(\displaystyle S\) and \(\displaystyle R\), respectively. The lines \(\displaystyle PS\) and \(\displaystyle QR\) meet at \(\displaystyle E\). The second intersection point of the circles \(\displaystyle PQE\) and \(\displaystyle RSE\), other than \(\displaystyle E\), is \(\displaystyle M\). The points \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\), \(\displaystyle E\), \(\displaystyle M\), \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), \(\displaystyle S\), \(\displaystyle U\), \(\displaystyle V\) are distinct. Show that the center of the circle \(\displaystyle BCD\), the center of the circle \(\displaystyle AUV\) and the point \(\displaystyle M\) are collinear.
(5 pont)
A. 691. Let \(\displaystyle c\ge3\) be an integer, and define the sequence \(\displaystyle a_1,a_2,\dots\) by the recurrence \(\displaystyle a_1=c^2-1\), \(\displaystyle a_{n+1}=a_n^3-3a_n^2+3\) \(\displaystyle (n=1,2,\ldots)\). Show that for every integer \(\displaystyle n\ge2\), the number \(\displaystyle a_n\) has a prime divisor that does not divide any of \(\displaystyle a_1,\ldots,a_{n-1}\).
(5 pont)
Upload your solutions above.
