KöMaL Problems in Physics, March 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on April 10, 2017. |
M. 367. Make cylinder-shaped ice sticks. (For example in the deep-freezer freeze water in closed plastic tubes.) At their midpoint gradually load the ice sticks, which are supported at their ends, until they break. Determine the force at which the sticks, which have different lengths and diameters, break.
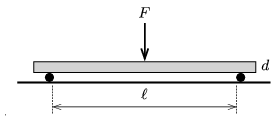
(6 pont)
 |
Problems with sign 'G'Deadline expired on April 10, 2017. |
G. 596. From the ground floor of a house we climb the stairs to the top floor and then we use the lift to come down. This takes 4 minutes. It would take 3 minutes to use the lift in the upward direction and then climb down the stairs. It would take only one minute to go up and down in the lift.
How long would it take to climb up and down the stairs?
(3 pont)
solution (in Hungarian), statistics
G. 597. A solid cube is floating in a container filled with some liquid. The system is heated slowly. Hasty Tymothy states that the cube will slowly sink. Sudden Lily immediately replies that on the contrary it will rise. Who is right?
(3 pont)
solution (in Hungarian), statistics
G. 598. A piece of ice having temperature \(\displaystyle 0\,{}^\circ\)C is thrown into a thermally insulated container, filled with water of volume \(\displaystyle 5~{\rm dm}^3\) at a temperature of \(\displaystyle 50\,{}^\circ\)C. What is the final amount of water in the container if after the ice melts the temperature of the system is \(\displaystyle 15\,{}^\circ\)C?
(3 pont)
 |
Problems with sign 'P'Deadline expired on April 10, 2017. |
P. 4916. There is a slope of height \(\displaystyle H\) and of elevation angle of \(\displaystyle \alpha\) at rest on the level ground. There is a small point-like object next to the slope. At what acceleration must the slope be moved in order that the point-like object reaches its top in a time of \(\displaystyle t\)? (Friction is negligible.)
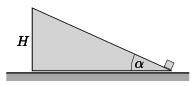
Data: \(\displaystyle \alpha=30^\circ\), \(\displaystyle H=0.2\) m, \(\displaystyle t=0.2\) s.
(4 pont)
solution (in Hungarian), statistics
P. 4917. On a horizontal half-plane the coefficient of friction is proportional to the distance measured from the boundary line of the half-plane: \(\displaystyle \mu=k\cdot x\). A small flat object starts to move from this line perpendicularly to it at an initial speed of \(\displaystyle v_0\). When and where will it stop?
Data: \(\displaystyle v_0=2~\frac{\rm m}{\rm s}\), \(\displaystyle k=0.4~\frac{1}{\rm m}\).
(4 pont)
solution (in Hungarian), statistics
P. 4918. A plane approaches the runway at a speed of \(\displaystyle v\). The depression angle of the gliding is \(\displaystyle \alpha\). When it is at a height of \(\displaystyle H\) above the ground, it leaves the straight path and follows a circular trajectory along which its speed remains \(\displaystyle v\). When it reaches the runway it just flies horizontally.
\(\displaystyle a)\) What is the radius of the circular trajectory?
\(\displaystyle b)\) For how long does the plane fly along the circular arc?
\(\displaystyle c)\) At most what is the percent increase of the weight of the pilot?
Data: \(\displaystyle v=70~{\rm m}/{\rm s}\), \(\displaystyle \alpha=3^\circ\), \(\displaystyle H=100\) m.
(4 pont)
solution (in Hungarian), statistics
P. 4919. A trolley of mass \(\displaystyle m_1\) was placed to a horizontal, rigid pair of rails at some height as shown in the figure. There is a small ball of mass \(\displaystyle m_2\) attached to one end of a thread, whose other end is attached to the bottom of the trolley. (The thread hangs between the rails. The length of the thread is much greater than the size of the ball and the trolley.)
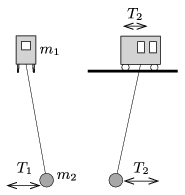
If the ball is displaced a bit from its stable equilibrium position in the direction perpendicular to the rails, then it swings with a period of \(\displaystyle T_1\). If the ball is displaced a bit parallel to the rails, while the trolley is fixed, and then both the ball and the trolley are released, then the period of the oscillation is \(\displaystyle T_2\). What is the ratio of \(\displaystyle m_2/m_1\), if \(\displaystyle T_1/T_2=2\)? (Friction and air drag are negligible.)
(5 pont)
solution (in Hungarian), statistics
P. 4920. A police car is approaching a stationary observer at a constant speed, and then it is moving away from it at the same constant speed.
\(\displaystyle a)\) What is the speed of the police car, if the observer detects that the sound of the siren of the car when it is approaching is higher by a minor third than the detected sound when it is moving away?
\(\displaystyle b)\) What is the percent decrease in the difference between the detected sound of the siren of the approaching and leaving police car for an observer, who is in another car travelling towards the police car from the front at a speed of 36 km/h?
The speed of sound is 330 m/s.
(4 pont)
solution (in Hungarian), statistics
P. 4921. Frictionless movable pistons are in a horizontal cylinder, closed at both ends, and confine samples of diatomic, ideal gas of the same type and of the same volume of \(\displaystyle V_0=2~\rm dm^3\) at a pressure of \(\displaystyle p_0=10^4\) Pa, and at the same temperature. The pistons are connected by a spring the length of which when it is not compressed or stretched is the same as the length of the cylinder. Between the pistons there is vacuum.
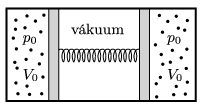
\(\displaystyle a)\) What is the energy stored in the spring in its compressed position described above?
\(\displaystyle b)\) The gas samples are heated slowly in the same way, and their absolute temperature is tripled. What will the pressure of the gas samples be at the end of the heating process?
\(\displaystyle c)\) How much heat was added to the system, if the losses are neglected?
(5 pont)
solution (in Hungarian), statistics
P. 4922. The electromotive force of a battery is \(\displaystyle \mathcal{E}=18\) V. There is a 0.2 A current through one of the two resistors connected in parallel, which has a resistance of \(\displaystyle R_x\), whilst the resistance of the other resistor is \(\displaystyle R=8~\Omega\). If this resistor is disconnected from the circuit by switching off switch K, then the current through the resistor \(\displaystyle R_x\) increases to 0.3 A. What is the resistance of the resistor, and what is the internal resistance of the battery?
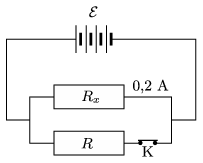
(5 pont)
solution (in Hungarian), statistics
P. 4923. An insulated metal disc of radius 0.250 m is rotating with 1000 revolutions per minute. Determine the potential difference between the rim of the disc and its centre if
\(\displaystyle a)\) there is no external magnetic field;
\(\displaystyle b)\) it is in uniform magnetic field of magnitude 10.0 mT, which is perpendicular to the plane of the disc.
(5 pont)
solution (in Hungarian), statistics
P. 4924. On a hot summer day the photo below was taken on the motorway. The lens of the camera was at a height of 1.8 m, and the nearest part of the mirage (resembling to the water of a puddle) seems to be at a distance of 180 m. Estimate the difference between the refractive index of the air next to the ground and that of at the level of the camera.

(4 pont)
solution (in Hungarian), statistics
P. 4925. Using the uncertainty principle estimate from below the energy of an electron enclosed into a sphere of diameter \(\displaystyle 10^{-11}\) m.
(4 pont)
solution (in Hungarian), statistics
P. 4926. An electron is released in vacuum from a point, which is equidistant from the three metal walls of a great corner, (orthogonal trihedron) at a distance of \(\displaystyle R=60\) cm from the vertex. How long does it take for the electron to fall into the vertex?
(6 pont)
Upload your solutions above.
