A KöMaL 2017. szeptemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
I. 433. Készítsünk programot i433 néven, amely egy szöveg karaktereit egy négyzet oldalán fényújságszerűen mozgatva jeleníti meg.
A program bemenete az \(\displaystyle \mathsf{S}\) szöveg (\(\displaystyle \mathop{\rm Hossz}{(\mathsf{S})}\le 100)\) és a négyzet \(\displaystyle N\) oldalhossza (\(\displaystyle \mathop{\rm Hossz}{(\mathsf{S})}/4\le N\le 60)\).
A program a karakteres vagy grafikus kimeneten jelenítse meg a fényújságot az óramutató járásának megfelelő irányban. A mozgatás sebességét válasszuk meg úgy, hogy a szöveg élvezhetően olvasható legyen. A szöveg mozgatása egy adott billentyű lenyomásáig folytatódjon.
| Példa bemenet | Kimenet | ||
|
|
Beküldendő egy tömörített i433.zip állományban a program forráskódja és rövid dokumentációja, amely megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható.
(10 pont)
I. 434. (É) A 2016. évi nyári olimpiai játékokon az atlétika férfi kalapácsvetés döntőjének eredményeit értékeljük ki táblázatkezelő-rendszerrel.
A döntő előtt a selejtező nevezési szintje 77,00 méter volt. Ezt csak ketten dobták túl, így a döntőbe a legjobb 12 eredményű versenyző jutott. A döntő 6 dobási sorozatból állt, de a 3. sorozat után csak az addigi legjobb 8 eredményt elért versenyző folytathatta tovább. A dobás távolságát centiméter pontossággal mérik. Ha a dobás érvénytelen volt, akkor az eredmény helyén az ,,\(\displaystyle \textsf{x}\)'' karakter szerepel.
A döntőbe jutott versenyzők dobási adatait rögzítettük méterben a kalapacsforras.txt tabulátorral tagolt, UTF-8 kódolású állományban.
1. Töltsük be a kalapacsforras.txt szövegfájlt a táblázatkezelő egy munkalapjára az \(\displaystyle \textsf{A1}\)-es cellától kezdődően. Munkánkat \(\displaystyle \texttt{i434}\) néven mentsük el a táblázatkezelő alapértelmezett formátumában.
2. A \(\displaystyle \textsf{J2:J13}\) tartomány celláiban írassuk ki a versenyzők legjobb dobásainak távolságát, azaz a versenyen elért eredményüket.
3. Az \(\displaystyle \textsf{A2:A13}\) tartomány celláiban egyetlen képlettel és annak másolásával határozzuk meg a versenyzők helyezését.
4. Az első három sorozat után az addigi legjobb 8 eredményt elérő versenyző folytathatja a versenyt. Az \(\displaystyle \textsf{M3}\) cellában adjuk meg a verseny folytatásához szükséges dobástávolságot.
5. Az \(\displaystyle \textsf{M2}\) cellában a selejtező nevezési szintje szerepel. Határozzuk meg függvény segítségével, hogy a verseny összes résztvevője közül hányan teljesítették ezt.
6. Az \(\displaystyle \textsf{M5}\) cellában képlettel adjuk meg, hogy a döntő összes dobásának hány százaléka volt érvénytelen.
7. Az \(\displaystyle \textsf{M6}\) cellában határozzuk meg, hogy a 3. sorozat után még versenybe maradók hány százaléka tudott még a további dobásokkal az eredményén javítani.
8. Az \(\displaystyle \textsf{M2:M6}\) cellatartományban állítsuk be a mértékegységeket.
9. Az \(\displaystyle \textsf{A15:C22}\) tartomány celláiban függvények segítségével jelenítsük meg a végeredményt, soroljuk fel helyezési sorrendben a versenyzők nevét és országát.
10. A \(\displaystyle \textsf{D2:I13}\) cellatartományban minden versenyző legnagyobb dobását feltételes formázással, félkövér betűstílussal jelenítsük meg.
11. Az \(\displaystyle \textsf{A2:J13}\) cellatartományban az első három helyezett sorának celláiban a cellakitöltését az érem színének megfelelően feltételes formázással adjuk meg: arany RGB(255,215,0), ezüst RGB(192,192,192), bronz RGB(204,153,102).
Minta:
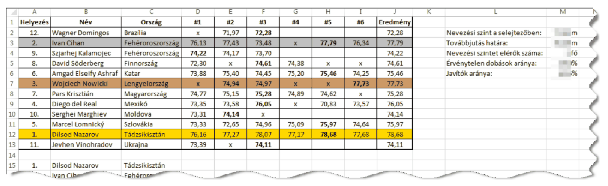
Beküldendő egy i434.zip tömörített állományban a megoldást tartalmazó munkafüzet, valamint egy rövid dokumentáció, amelyből kiderül az alkalmazott táblázatkezelő neve és verziószáma.
A munkafüzetbe importálandó adattábla: a kalapacsforras.txt.
(10 pont)
I. 435. Mint ismeretes, az Európában is használatos keresztény naptár szerinti 1. év Jézus születésének éve, és Gergely pápa naptárreformjáig a ma használatostól csak annyiban tért el, hogy minden negyedik év szökőév volt. A Gergely-naptár 1582. október 4-én csütörtökön lépett életbe úgy, hogy az azt követő nap október 15. péntek lett, és ettől kezdve a 100-zal osztható évszámok közül csak a 400-zal is oszthatók maradtak szökőévek. A keresztény időszámítás így a Nap járásához igazodik.
Az iszlám naptár a Hold járásán alapuló éveket használó holdnaptár, melynek kezdőnapja (a keresztény időszámítás szerint) 622. július 16. Ez az iszlám időszámítás kezdete, vagyis az 1. év 1. hónapjának (Muharram hónap) 1-je. (Az iszlám időszámítás a hidzsráról kapta a nevét, amelynek jelentése: kivándorlása, áttelepülése – bár az esemény, vagyis Mohamed próféta Mekkából való kivonulása valójában néhány hónappal később történt.)
A hónapok felváltva 30 (páratlan számú hónapok) és 29 naposak (páros számúak). Az éveket 30 éves ciklusokba sorolják. E ciklusokban 19 normál év (354 napos) található, míg a 2., 5., 7., 10., 13., 16., 18., 21., 24., 26. és 29. év 355 napos. Ezekben az években az utolsó hónap is 30 napból áll.
A két dátum összevetésére itt találunk egy példát:
https://calendar.zoznam.sk/islamic_calendar-hu.php.
Készítsünk táblázatkezelővel táblázatot vagy írjunk programot, amely egy hidzsra utáni iszlám dátumot átvált keresztény dátumra és fordítva. Például: 1439.01.01 – 2017.09.22.
Beküldendő egy i435.zip tömörített állományban a táblázatkezelő munkafüzet vagy a program forráskódja, továbbá a dokumentáció, amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztői környezetben fordítható vagy milyen táblázatkezelővel készült.
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
I/S. 19. Keressük meg azt a legkisebb \(\displaystyle b\) nevezőjű \(\displaystyle \frac{a}{b}\) törtet, amelynek \(\displaystyle t\) tizedes jegyre kerekített értéke megegyezik egy \(\displaystyle t\) tizedes jegyet tartalmazó \(\displaystyle r\) tizedes törttel.
A feladatot megoldó program olvassa be a standard bemenetről \(\displaystyle r\) és \(\displaystyle t\) szóközzel elválasztott értékét (tizedesvessző helyett pontot használjunk), majd írja a standard kimenet egyetlen sorába szóközzel elválasztva \(\displaystyle a\) és \(\displaystyle b\) egészeket.
Példák:
| Bemenet | Kimenet |
| 3.141592653 9 | 103993 33102 |
| 2017.0901 4 | 223897 111 |
| 1.2345678901234 13 | 2743458 2222201 |
Korlátok: az \(\displaystyle r\) pozitív szám \(\displaystyle e\) egész és \(\displaystyle t\) tizedes jegyet tartalmaz \(\displaystyle (1 \le e,t \le 14)\), \(\displaystyle (1 \le e+t \le 15)\).
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra programra, amely csak kisebb \(\displaystyle e\), \(\displaystyle t\) értékek esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy is19.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2017. október 10-én LEJÁRT. |
S. 118. Egy tengeren adott \(\displaystyle N\) sziget, melyek kiterjedése elhanyagolható a tenger méreteihez képest. Az \(\displaystyle i\)-edik \(\displaystyle (1 \le i \le N)\) sziget helyzetét derékszögű koordináta-rendszerben az \(\displaystyle (X_i, Y_i)\) egész számpárral adjuk meg \(\displaystyle (0 \le X_i, Y_i \le 10\,000)\). Az egyik szigetről egy másik szigetre szeretnénk eljutni. Bármely két sziget között hajóval lehet az utat megtenni. A hajók bármely szigeten tudnak üzemanyagot tankolni, amellyel egy adott távolságig tudnak közlekedni. Keressük meg, hogy mekkora az a legkisebb hatótávolságú hajó, amellyel az utazás a két kiválasztott sziget között biztosítható.
A feladatot megoldó program olvassa be a standard bemenet első sorából \(\displaystyle N\) értékét \(\displaystyle (N \le 1\,000)\) , majd a következő \(\displaystyle N\) sorból az \(\displaystyle X_i\), \(\displaystyle Y_i\) szóközzel elválasztott számokat, végül az utolsó sorból az utazás induló és érkező szigetének sorszámát. A program írja a standard kimenetre a legkisebb hatótávolság öt tizedes jegyre kerekített értékét.
Példa:
| Bemenet | Kimenet |
|---|---|
5 4 9 1 8 6 5 3 3 2 5 1 5 |
3.16228 |
Értékelés: a megoldás lényegét leíró dokumentáció 1 pontot ér. További 9 pont kapható arra a programra, amely a korlátoknak megfelelő bemenetekre helyes kimenetet ad 1 másodperc futásidő alatt. Részpontszám kapható arra programra, amely csak kisebb \(\displaystyle N\) érték esetén ad helyes eredményt 1 másodpercen belül.
Beküldendő egy s118.zip tömörített állományban a megoldást leíró dokumentáció és a program forráskódja.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

