A KöMaL 2017. októberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2017. november 10-én LEJÁRT. |
K. 553. András és Vili egy zsákból húznak, amiben cetliken a számok vannak 1-től 200-ig. Felváltva kihúzzák az összeset, majd a végén összeadják számaikat. Ha első húzásra András 3-at, Vili 170-et húzott, akkor legfeljebb mennyivel lehet András összege nagyobb Vili összegénél?
(6 pont)
K. 554. Leírjuk az egész számokat 1-től 2017-ig a következőképpen. Először leírjuk növekvő sorrendben azokat, amelyek nem oszthatók 3-mal. Majd pedig, amelyek oszthatók 3-mal, de nem oszthatók 9-cel, utána azokat, amelyek oszthatók 9-cel, de nem oszthatók 27-tel, és így tovább.
\(\displaystyle a)\) Mi az utolsóként leírt szám?
\(\displaystyle b)\) Hányadikként írtuk le a 2017-et?
\(\displaystyle c)\) Hányadikként írtuk le a 2016-ot?
(6 pont)
K. 555. Melyik az a három szomszédos egész szám, amelyek szorzata éppen az összegük ötszöröse?
(6 pont)
K. 556. Az egységoldalú négyzetekből álló négyzetrácson lehet-e olyan ötszöget készíteni, amelynek minden csúcsa rácspont és minden oldala \(\displaystyle \sqrt 5\) hosszúságú?
(6 pont)
K. 557. Egy \(\displaystyle ABCD\) négyzet \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) és \(\displaystyle S\) oldalfelező pontjait összekötöttük a négyzet csúcsaival az ábrán látható módon. Bizonyítsuk be, hogy \(\displaystyle AT = TV\).
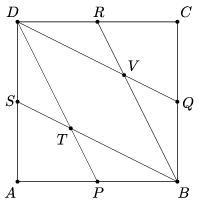
(6 pont)
K. 558. Mely \(\displaystyle n\) pozitív egész számok esetén lesz \(\displaystyle n^{4}+n^{2}+1\) prímszám?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2017. december 11-én LEJÁRT. |
C. 1434. Egy Münchenben megrendezett futóversenyen a versenyzők egyszerre rajtoltak és kijelölt pályán haladtak. A rajt után 30 perccel, a rajtvonalról utánuk indult egy elfogó autó, állandó sebességgel. Egy versenyző számára akkor ért véget a verseny, ha az elfogó autó utolérte. A női győztest 68 km-nél érte utol az autó, a férfi győztest pedig 1 óra 36 perccel később 92 km-nél. Milyen sebességgel haladt a két győztes futó és az elfogó autó, ha feltételezzük, hogy a futók sebessége is végig állandó volt?
(5 pont)
C. 1435. Egy 2 egység oldalú négyzet két szomszédos oldala, mint átmérő fölé befelé félköröket rajzolunk. Határozzuk meg az egyik félkört és a négyzet oldalát belülről érintő, a másik félkört pedig kívülről érintő kör sugarát.
Javasolta: Fülöp Dóra (Pécs)
(5 pont)
C. 1436. Nyolc piros és nyolc fehér színű egybevágó kiskockából kiválasztunk nyolcat, és ezekből egy nagy kockát rakunk össze. Hányféle színezésű nagy kockát kaphatunk? Két kocka különböző színezésű, ha forgatással nem vihetők egymásba.
Matlap (Kolozsvár)
(5 pont)
C. 1437. Októberi számunkban a feladat hibásan jelent meg. A feladatot újra kitűzzük; a novemberi feladatokkal együtt küldhető be.
Kilenc különböző egyenes mindegyike \(\displaystyle 2:3\) arányban osztja egy négyzet területét úgy, hogy egyik egyenes sem vág le háromszög alakú részt a négyzetből. Igazoljuk, hogy az egyenesek között van három olyan, amelyek egy ponton mennek keresztül.
(5 pont)
C. 1438. Bizonyítsuk be, hogy az \(\displaystyle x^2+y^3=z^4\) egyenletnek nincs megoldása az \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) prímszámok körében.
(5 pont)
C. 1439. Milyen \(\displaystyle c\) érték esetén lesz az
\(\displaystyle {(x-5)}^2+ {(y-1)}^2 =c,\)
\(\displaystyle {(x-1)}^2+ {(y-5)}^2 =c\)
egyenletrendszernek egyetlen megoldása?
(5 pont)
C. 1440. Az \(\displaystyle ABCDA'B'C'D'\) egységkockában legyenek \(\displaystyle M\) és \(\displaystyle N\) a \(\displaystyle D'\) és \(\displaystyle B\) pontok merőleges vetületei a \(\displaystyle B'D\) testátlóra. Határozzuk meg a \(\displaystyle BND'M\) négyszög területét.
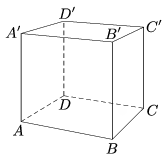
Matlap (Kolozsvár)
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2017. november 10-én LEJÁRT. |
B. 4894. Hét rabló a zsákmányolt aranytallérokat úgy osztja el, hogy névsor szerint haladva annyit vesznek el, amennyi a még nem szétosztott aranytallérok számában a számjegyek összege. Két teljes kör után az arany elfogy. Mindenkinek ugyanannyi jutott, csak a vezérnek lett több. Hányadik volt a vezér a névsorban?
Matlap (Kolozsvár)
(4 pont)
B. 4895. Bizonyítsuk be, hogy ha \(\displaystyle n-1\) és \(\displaystyle n+1\) egyaránt prímszámok, és \(\displaystyle n> 6\) egész szám, akkor \(\displaystyle n^2(n^2+16)\) osztható 720-szal.
(3 pont)
B. 4896. Az \(\displaystyle ABCD\) konvex négyszög oldalfelező pontjai legyenek \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), \(\displaystyle D_1\). Az \(\displaystyle A_1B_1C_1D_1\) négyszög oldalfelező pontjai legyenek \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\), \(\displaystyle D_2\) és ezt folytatjuk tovább. Bizonyítsuk be, hogy ha \(\displaystyle A_1B_1C_1D_1\) húrnégyszög, akkor \(\displaystyle A_{2017}B_{2017}C_{2017}D_{2017}\) is húrnégyszög.
Javasolta: Szoldatics József (Budapest)
(3 pont)
B. 4897. Adott a síkon \(\displaystyle n\) darab pont. Mutassuk meg, hogy kiválasztható közülük három – mondjuk \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\) – úgy, hogy \(\displaystyle ABC\sphericalangle\le 180^\circ /n\).
(4 pont)
B. 4898. Bizonyítsuk be, hogy ha \(\displaystyle A\) egy pozitív egész számokból álló négyelemű halmaz, hogy bármely \(\displaystyle a,b\in A\), \(\displaystyle a\ne b\) esetén \(\displaystyle ab+13\) négyzetszám, akkor \(\displaystyle A\) elemei 4-gyel osztva 2-t adnak maradékul. (Lásd Diofantoszi számhalmazok című cikkünket a 391. oldalon.)
Javasolta: Nyul Gábor (Debrecen)
(4 pont)
B. 4899. A \(\displaystyle G\) egyszerű síkgráf minden csúcsa harmadfokú, és tudjuk, hogy létezik \(\displaystyle G\)-nek olyan síkba rajzolása, ahol \(\displaystyle G\) élei egymást nem metsző egységnyi hosszú szakaszok. Mutassuk meg, hogy \(\displaystyle G\)-nek legalább \(\displaystyle 8\) csúcsa van.
(5 pont)
B. 4900. Legyen \(\displaystyle K\) egy origóra szimmetrikus konvex lemez, \(\displaystyle e\) egy origóra illeszkedő egyenes, \(\displaystyle e'\) pedig egy tetszőleges, \(\displaystyle e\)-vel párhuzamos egyenes. Jelölje továbbá \(\displaystyle \# H\) a \(\displaystyle H\) halmazba eső rácspontok számát. Igazoljuk, hogy \(\displaystyle \# (K\cap e)+1 \ge \# (K\cap e')\).
(5 pont)
B. 4901. Törpfalván járvány ütötte fel a fejét azt követően, hogy csúf kórság fertőzött meg néhány törpöt. Szerencsére a betegségből minden törp egy nap alatt meggyógyul, és ezután egy napig immunissá válik, ám sajnos ezt követően újra fertőződhet. Az állapot megváltozása mindig éjszaka, alvás közben következik be. Kellemetlen, hogy a törpök még betegen sem adják fel azt a megrögzött szokásukat, hogy minden egyes nap minden barátjukat meglátogatják. Márpedig ha egy beteg törp egy nem immunis, egészséges törppel találkozik, az utóbbi bizonyosan megfertőződik. Mutassuk meg, hogy ha Törpfalván 100 törp él, akkor a járványnak a kitörését követő 101. napon már biztosan vége van.
BME VIK folklór
(6 pont)
B. 4902. Adott a síkon négy különböző hosszúságú, egymással párhuzamos szakasz, \(\displaystyle A_1B_1\), \(\displaystyle A_2B_2\), \(\displaystyle A_3B_3\) és \(\displaystyle A_4B_4\). Tetszőleges \(\displaystyle 1\le i<j\le 4\) esetén legyen \(\displaystyle M_{ij}\) az \(\displaystyle A_iB_j\) és \(\displaystyle A_jB_i\) egyenesek metszéspontja. Mutassuk meg, hogy az \(\displaystyle M_{12}M_{34}\), \(\displaystyle M_{13}M_{24}\) és \(\displaystyle M_{14}M_{23}\) egyenesek egy ponton mennek át vagy párhuzamosak.
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2017. november 10-én LEJÁRT. |
A. 704. Egy \(\displaystyle n\) hosszú oldalakkal rendelkező szabályos háromszög oldalainak \(\displaystyle n\)-edelőpontjain át behúztuk az oldalakkal párhuzamos egyenesek háromszögbe eső szakaszait. Tekintsük az így létrejövő \(\displaystyle 1+2+\ldots+(n+1)\) darab metszéspont alkotta pontrácsot. Melyek azok az \(\displaystyle n\) pozitív egészek, melyekre ez a pontrács olyan ponthármasokba partícionálható, melyek egy-egy egységnyi oldalú szabályos háromszög csúcsai?
Javasolta: Alexander Gunning (Cambridge, Egyesült Királyság)
(5 pont)
A. 705. Legyen az \(\displaystyle ABC\) háromszög magasságpontja \(\displaystyle H\), és legyen \(\displaystyle D\) egy, a csúcsoktól különböző pont a háromszög körülírt körén. Tegyük fel, hogy a \(\displaystyle BHD\) kör az \(\displaystyle AB\) egyenest \(\displaystyle P\ne B\)-ben, illetve a \(\displaystyle CHD\) kör az \(\displaystyle AC\) egyenest \(\displaystyle Q\ne C\)-ben metszi. Mutassuk meg, hogy a \(\displaystyle D\) pontot a körülírt körön mozgatva, \(\displaystyle D\)-nek \(\displaystyle PQ\)-ra vonatkozó tükörképe is egy rögzített körön mozog.
Javasolta: Michael Ren (Andover, Massachusetts, USA)
(5 pont)
A. 706. Jelölje \(\displaystyle \mathbb{Z}^+\) a pozitív egészek halmazát. Határozzuk meg az összes olyan \(\displaystyle f\colon \mathbb{Z}^+\to\mathbb{Z}^+\) függvényt, melyre a következők teljesülnek:
\(\displaystyle \bullet\) \(\displaystyle f(mn)=f(m)f(n)\) minden \(\displaystyle m,n\in\mathbb{Z}^+\)-ra, illetve
\(\displaystyle \bullet\) \(\displaystyle f^{(n)}(n)=n\) minden \(\displaystyle n\in\mathbb{Z}^+\)-ra (azaz \(\displaystyle f\Big(f\big(\ldots\big(f(n)\big)\dots\big)\!\Big)=n\), ahol a zárójelpárok száma \(\displaystyle n\)).
Koreai feladat
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

