KöMaL Problems in Mathematics, March 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on April 11, 2005. |
K. 37. At the confectioner's, we bought 5 pieces of candy in a paper bag, and 10 pieces in another, identical bag. (Each piece of candy has the same mass.) The first bag was weighed to be 85 grams and the second one 165 grams. How much did we pay for a paper bag if the candy cost 1200 forints (HUF) a kilo.
(6 pont)
solution (in Hungarian), statistics
K. 38. An octagon is inscribed in a circle. Determine the sum of four interior angles, no pair of which are adjacent.
(6 pont)
solution (in Hungarian), statistics
K. 39. The perimeter of a convex quadrilateral ABCD is cut at each vertex, and the four sides are parallel shifted to a common point O as shown in the Figure The endpoints of the line segments different from O are connected to form the quadrilateral XYZV. By what factor is the area of the quadrilateral XYZV greater than that of the original quadrilateral ABCD?
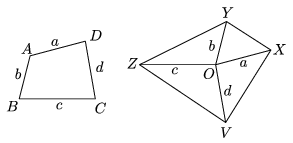
(6 pont)
solution (in Hungarian), statistics
K. 40. In a jeep there are 3 seats in front and 3 in the back. In how many different ways can six persons of different heights be seated in the jeep, so that everyone in front is shorter than the person directly behind. (Each of them is allowed to sit in the driver's seat.)
(6 pont)
solution (in Hungarian), statistics
K. 41. The half of the square of an integer and one sixth of the cube of the same integer are added to one third of the same integer. Prove that the result is an integer.
(6 pont)
solution (in Hungarian), statistics
K. 42. There are two tribes living in Binumeria. The two tribes use numbers expressed in different notations, but the base of each notation is smaller than ten. We asked one man from each tribe how many people there were in the tribe. They both answered 10011, and one of them added that the other tribe had 10 more members and that 1+2=3. How many people live in Binumeria?
(6 pont)
 |
Problems with sign 'C'Deadline expired on April 15, 2005. |
C. 800. Find those positive integers that are 14 times larger than the sum of their decimal digits.
(5 pont)
solution (in Hungarian), statistics
C. 801. There is a rectangle inscribed in the pythagorean triangle whose sides are 3, 4, 5 units long, respectively. The vertices of the rectangle are incident to the sides of the triangle and the ratio of its perpendicular sides is 1:3. Determine the dimensions of the rectangle.
(5 pont)
solution (in Hungarian), statistics
C. 802. We want to prepare a folding rectangular dining table which when closed is in the position ABCD, when rotated about a pin by ninety degrees is in the position A'B'C'D' and it arrives to the position B1B'C'C1 when unfolded. (See the figure.)
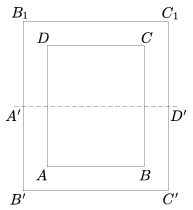
Where shall we put the pin about which the table rotates? How shall we set the dimensions of the table ABCD if, in case of a big fat dinner an even larger table could be produced from the position B1B'C'C1 by repeating the previous procedure, i.e. rotating the table by right angle about the very same pin and unfolding it once more? (Proposed by Papp Zoltán Dániel, Szeged)
(5 pont)
solution (in Hungarian), statistics
C. 803. Solve the simultaneous equations
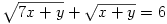
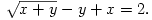
(5 pont)
solution (in Hungarian), statistics
C. 804. The first term of a geometric progression is 6, the sum of the first n terms is 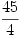 and the sum of the reciprocals of the same terms is equal to
and the sum of the reciprocals of the same terms is equal to 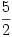 . Find this geometric progression.
. Find this geometric progression.
(5 pont)
 |
Problems with sign 'B'Deadline expired on April 15, 2005. |
B. 3802. Given are seven real numbers in such a way that the sum of any three of them is less than the sum of the remaining four. Show that each number is positive.
(3 pont)
solution (in Hungarian), statistics
B. 3803. Are there three cubes whose edges are integers and the sum of their volumes is equal to 1020+30?
(3 pont)
solution (in Hungarian), statistics
B. 3804. I have some coins in my pocket. One of them is a 1 penny coin and a few more (there are at least four of them) are 2 penny coins. I start drawing them randomly, one by one without replacement, and stop if the sum is a positive multiple of 3. How many drawings are necessary for that on the average?
(4 pont)
solution (in Hungarian), statistics
B. 3805. The lengths of the sides of a cyclic quadrilateral are a, b, c, d, respectively, its perimeter is 2s and the measure of the angle of the sides a and b is  . Prove that
. Prove that
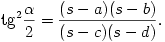
(4 pont)
solution (in Hungarian), statistics
B. 3806. Given are two disjoint circular discs in the plane. There are also given two diameters, respectively, which, when extended are touching the other circle. Prove that the endpoints of these diameters form a trapezium.
(4 pont)
solution (in Hungarian), statistics
B. 3807. The degree of each vertex of a graph is equal to 3 and it is also given that the graph does not contain cycles whose length is less than 6. Find the lowest possible number of vertices in such a graph.
(5 pont)
solution (in Hungarian), statistics
B. 3808. The real numbers x and y are both in the interval [0;12] and satisfy xy=(12-x)2(12-y)2. Find the maximum value of the product xy.
(5 pont)
solution (in Hungarian), statistics
B. 3809. The triangle ABC is isosceles, namely AB = BC. The points C1, A1, B1 lie on the sides AB, BC, CA, respectively, and such that  BC1A1=
BC1A1= CA1B1=
CA1B1= CAB. The lines BB1 and CC1 meet at P. Prove that the quadrilateral AB1PC1 is cyclic.
CAB. The lines BB1 and CC1 meet at P. Prove that the quadrilateral AB1PC1 is cyclic.
(4 pont)
solution (in Hungarian), statistics
B. 3810. Denote the greatest odd divisor of the positive integer n by k(n). Let
A(n)=k(1)+k(2)+...+k(n), B(n)=1+2+...+n.
Prove that there are infinitely many values of n such that 3 A(n) = 2B(n).
(5 pont)
solution (in Hungarian), statistics
B. 3811. Find the radius of the sphere inscribed into a four sided pyramid whose edges are 1 unit long each.
(3 pont)
 |
Problems with sign 'A'Deadline expired on April 15, 2005. |
A. 368. The interior bisector of the angle A of the triangle ABC cuts the incircle c at two points; the one closer to A is denoted by OA. Define the points OB and OC similarly on the internal bisectors of the angles B and C, respectively. The circle cA is drawn about OA and it is touching the sides AB and CA. Similarly, cB is about OB and it is touching the sides BC and AB, finally the circle cC is about OC and it is touching the sides CA and BC. Taken any two of the circles cA, cB and cC consider their common external tangents different from the corresponding sides of the triangle, respectively. Prove that these three tangents are concurrent.
(5 pont)
A. 369. Find those positive integers n for which
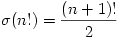
holds.
(5 pont)
A. 370. For any two guests on a party of kn participants there is some guest who knows both of them. Prove that if 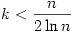 then one can find n guests who together know everyone else.
then one can find n guests who together know everyone else.
(5 pont)
Upload your solutions above.
