Competitions Portal

Problems in Mathematics, March 2007

Please read the rules of the competition.

Problems sign 'A'

Deadline expired.

A. 422. Let x₁,x₂,...,x_n,x_n+1 be positive real numbers with x₁+x₂+...+x_n=x_n+1. Prove that

$\sum_{i=1}^n\sqrt{x_i(x_{n+1}-x_i)} \le \sqrt{\sum_{i=1}^n x_{n+1}(x_{n+1}-x_i)}.$

Romanian competition problem

(5 points)

A. 423. Find all positive integers n for which the numbers $1,2,3,\ldots,2n$ can be colored with n colors such that each color is used exactly twice and each of the numbers $1,2,\ldots,n$ appear exactly once as the difference between two numbers with the same color.

German competition problem

(5 points)

A. 424. Given a convex quadrilateral ABCD and a point P in its interior such that AP=CP, $\measuredangle ABC=\measuredangle APD$ and $\measuredangle CDA=\measuredangle CPB$ . Prove that

DA^.AB^.BP=BC^.CD^.DP.

(5 points)

Problems sign 'B'

Deadline expired.

B. 3982. 100 freshly graduated mathematicians are looking for jobs. They consult two headhunter companies that have the same 100 positions to offer. Each company makes an offer to each applicant, a different one to each of them. Each applicant chooses from the two offers and, luckily, all positions are filled. Three months later, however, each of them decides to change for the job offered by the other company. (If it is the same as his actual job, then he decides to stay.) Show that all positions will be filled again.

Suggested by B. Csajbók (Budapest)

(3 points)

Solution (in Hungarian)

B. 3983. A few players are fighting a paintball battle. At a certain time instant, their distances from each other are all different. Then everyone shoots at the person who is closest to them. Is it possible for the paths of the projectiles to intersect each other?

(3 points)

Solution (in Hungarian)

B. 3984. A square is dissected into acute-angled triangles. What is the minimum number of pieces?

(5 points)

Solution (in Hungarian)

B. 3985. The lawn in our garden consists of n blades of glass. We want to cut the grass so that each blade of glass becomes equal in length but the total length of them stays the same. We are allowed to make n-1 cuts on the grass blades altogether, and we may fix the cut pieces to each other and to the remaining pieces. Is it always possible to complete the grass cutting in this way?

(4 points)

Solution (in Hungarian)

B. 3986. Let s(m) denote the number of digits of m for any positive integer m. Find all positive integers n, such that no digit of it is zero and

s(n²)=2^s(n).

Suggested by E. Dobribán, (Cluj-Napoca, Romania)

(4 points)

Solution (in Hungarian)

B. 3987. Let n $\ge$ 4 be an integer, and let $a_1,a_2,\ldots,a_n$ denote nonnegative real numbers. Prove that

${(a_1+a_2+a_3)}^2 {(a_2+a_3+a_4)}^2\cdot \ldots \cdot {(a_{n-1}+a_n+a_1)}^2{(a_n+a_1+a_2)}^2$

$\ge 2^n{(a_1+a_2)}^2{(a_2+a_3)}^2\cdot \ldots \cdot {(a_{n-1}+a_n)}^2{(a_n+a_1)}^2.$

Discuss also the case of equality.

(5 points)

Solution (in Hungarian)

B. 3988. The midpoints of the sides of a convex pentagon are F₁, F₂, F₃, F₄, F₅, in this order. (The vertex A is between F₅ and F₁.) Let P be the point in the plane for which the quadrilateral PF₂F₃F₄ is a parallelogram. Prove that the quadrilateral PF₅AF₁ is also a parallelogram.

(3 points)

Solution (in Hungarian)

B. 3989. a, b, c are positive numbers, such that a²+b²+c²+abc=4. Prove that a+b+c $\le$ 3.

(5 points)

Solution (in Hungarian)

B. 3990. Prove that in a right-angled triangle the intersections of the bisectors of the acute angles with the circumscribed circle are collinear with the points where the inscribed circle touches the legs.

(4 points)

Solution (in Hungarian)

B. 3991. The isosceles triangle ABC has a right angle at C. Let P be an arbitrary point of side BC, and let G denote the orthogonal projection of the point C onto AP. Let H be the point of the line segment AP for which AH=CG. Find the angle subtended by the line segment GH at the midpoint of AB.

(3 points)

Solution (in Hungarian)

Problems sign 'C'

Deadline expired.

C. 890. Find all pairs of natural numbers whose product is five times their difference.

(5 points)

Solution (in Hungarian)

C. 891. What maximum number of sides may a convex polygon have in which the interior angles form an arithmetic progression wit a common difference of d=1^o?

(5 points)

Solution (in Hungarian)

C. 892. Prove that if x, y, z are positive real numbers and xyz=1, then the values of the expressions

$\frac{1}{1+x+xy},\qquad \frac{y}{1+y+yz},\qquad \frac{xz}{1+z+xz}$

cannot all be greater than $\frac{1}{3}$ .

(5 points)

Solution (in Hungarian)

C. 893. We have sixteen painted Easter eggs. Three of them are red. We place ten eggs in a larger box and six in a smaller box in a random arrangement. What is the probability that there will be a red egg in each box?

(5 points)

Solution (in Hungarian)

C. 894. A hemispherical soup bowl has a volume of 8 litres. How much soup will fill the bowl to half its height?

(5 points)

Solution (in Hungarian)

Problems sign 'K'

Deadline expired.

K. 121. An arbitrary point is selected on each side of a rectangle. On what condition will the area of the quadrilateral formed by the four points be the half of the area of the rectangle?

Suggested by B. Szalkai (Veszprém)

(6 points)

Solution (in Hungarian)

K. 122. Draw a line segment AB on the plane and investigate the number of points on each line of the plane that form an isosceles triangle with the line segment AB. Define that number as the ``isosceles number'' of the line. Find all possible ``isosceles numbers''.

(6 points)

Solution (in Hungarian)

K. 123. Three bunnies are sitting in the grass. There is a heap of carrots in front of each of them, 36 carrots altogether. Suppose they simultaneously pass some carrots to one another: the first bunny passes one third of his carrots to the second one, the second one passes one fourth of his carrots to the third one, and the third bunny passes one fifth of his carrots to the first one. As a result, each bunny will have the same amount of carrots as initially. How many carrots does each of them have?

(6 points)

Solution (in Hungarian)

K. 124. ``Maci sajt'' is a brand name of processed cheese that comes in a round box containing eight individually wrapped sectors that just fit in the box. Stevie ate two sectors for breakfast, and arranged the remaining ones in the box as shown in the figure. His mom did not like that. She said that Stevie was squeezing the cheese pieces. Stevie insisted that there was no squeezing, the pieces just fit. Who was right?

Suggested by G. Kós (Budapest)

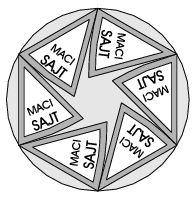
(6 points)

Solution (in Hungarian)

K. 125. Sebastian and Vincent were building towers out of wooden building blocks. They both used identical prisms of square base. Sebastian laid the blocks on each other along their faces of smaller area, while Vincent laid them on each other along their faces of larger area. Sebastian's tower of four blocks turned out to have the same height as Vincent's tower of six blocks. Find the height of the towers, given that the sum of their base areas is 160 cm².

(6 points)

Solution (in Hungarian)

K. 126. There are one thousand rooms in the sultan's palace. In each room there is a switch that switches all the lamps in the room on or off. When the lamps were on in each room and the sultan was bored, he walked through all his rooms one by one and repeated his walk again and again, always starting with the first room. During the first walk, he turned all the switches. The second time he turned the switch in every second room. The third time he turned the switch in every third room, and so on. (He turned the light on if it was off, and he turned it off if it was on). When he had walked through his room 500 times, he got tired of the game and decided to go to bed. He needed a room in which the lights were off. Which rooms did he have to choose from?

Suggested by G. Bohner (Budapest)

(6 points)

Solution (in Hungarian)

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Our web pages are supported by:

ELTE