Competitions Portal

Problems in Mathematics, March 2008

Please read the rules of the competition.

Problems sign 'A'

Deadline expired.

A. 449. In the convex quadrilateral ABCD, denote by r_A, r_B, r_C and r_D the inradii of triangles BCD, CDA, DAB and ABC, respectively. Prove that the quadrilateral ABCD is cyclic if and only if r_A+r_C=r_B+r_D.

Chinese problem

(5 points)

A. 450. The function $f\colon \mathbb{R}\to \mathbb{R}$ satisfies the equation f(x+f(y))+f(f(x)+y)=2x+2y. Prove that f(2x)=2f(x) for all real numbers x.

(5 points)

A. 451. Let $\mathcal{U}\subset P(S)$ be an upset and let $\mathcal{D}\subset P(S)$ be a downset on a set S of n elements, i.e.

(a) for every $X\in\mathcal{U}$ we have $Y\in\mathcal{U}$ for all X $\subset$ Y $\subset$ S;

(b) for every $X\in\mathcal{D}$ and Y $\subset$ X, $Y\in\mathcal{D}$ .

Prove that $|\mathcal{U}| \cdot |\mathcal{D}| \ge 2^n \cdot |\mathcal{U}\cap\mathcal{D}|$ .

(5 points)

Problems sign 'B'

Deadline expired.

B. 4072. Let S(n) denote the sum of the digits of the natural number n. Prove that there are infinitely many natural numbers n not ending in 0, such that S(n²)=S(n).

Suggested by G. Holló, Budapest

(3 points)

Solution (in Hungarian)

B. 4073. Find all right-angled triangles, such that the sides are integers, and the sum of the legs is obtained by adding 6 to the hypotenuse.

(3 points)

Solution (in Hungarian)

B. 4074. C is a given point in the plane, and there is a given circle in the plane. If AB is a diameter of the circle, what is the locus of the orthocentres of triangles ABC?

(4 points)

Solution (in Hungarian)

B. 4075. Find the maximum of the function $f(x)=\sqrt{x-2} + \sqrt{2x-7} + \sqrt{18-3x}$ .

(3 points)

Solution (in Hungarian)

B. 4076. Lisa and Sam are playing the following game: Lisa marks a point L₁ on side AB of a given triangle ABC. Then Sam chooses a point S on side BC. Finally, Lisa marks a point L₂ on side CA. Lisa is trying to make the area of triangle L₁SL₂ as large as possible, and Sam is trying to make it as small as possible. What will be the area of triangle L₁SL₂ if both of them play as well as possible?

(4 points)

Solution (in Hungarian)

B. 4077. Prove that if the vertices of a nonagon are all lattice points then it has three vertices, such that the centroid of the triangle formed by them is also a lattice point.

(4 points)

Solution (in Hungarian)

B. 4078. a and n are positive integers, such that n>1 and $n\mid a^n-1$ . Prove that (a-1;n)>1.

(5 points)

Solution (in Hungarian)

B. 4079. Let G be a simple graph in which the longest path consists of k $\ge$ 3 edges and the degree of each vertex is at least k/2. Show that every edge of G belongs to a circuit. (A path is a sequence of linking edges that visits each vertex at most once.)

Suggested by T. Héger, Budapest

(4 points)

Solution (in Hungarian)

B. 4080. Three points are selected at random on a circle, independently of each other. What is the probability that the resulting triangle is acute-angled?

(4 points)

Solution (in Hungarian)

B. 4081. Prove that natural numbers can be coloured in 2008 colours, such that each colour occurs, and whenever 3a+5b=7c is true, there are two numbers among a, b and c that have the same colour.

(5 points)

Solution (in Hungarian)

Problems sign 'C'

Deadline expired.

C. 935. Is it possible to dissect a regular triangle into

a) 2007,

b) 2008 regular triangles?

(5 points)

Solution (in Hungarian)

C. 936. Find all positive integers that have as many factors divisible by six as factors not divisible by six.

Suggested by G. Holló, Budapest

(5 points)

Solution (in Hungarian)

C. 937. Three sides of a quadrilateral are $a=4\sqrt3$ , b=9 and $c=\sqrt3$ . Sides a and b enclose an angle of 30^o, and sides b and c enclose an angle of 90^o. What angle do the diagonals enclose?

(5 points)

Solution (in Hungarian)

C. 938. Solve the following equation on the set of pairs of integers: (x+2)⁴-x⁴=y³.

Suggested by D. Fülöp, Marcali

(5 points)

Solution (in Hungarian)

C. 939. A rectangle of sides 15 cm and 20 cm is rotated about a diagonal. What is the volume of the resulting solid of revolution?

(5 points)

Solution (in Hungarian)

Problems sign 'K'

Deadline expired.

K. 163. A team of eight members is paid 224 000 forints (Hungarian currency, HUF) for doing a certain job. The leader of the team (one of the eight members) gets 7 000 forints more than the average pay per member. Given that all the other members get the same amount, calculate how the sum is divided by the members of the team.

(6 points)

Solution (in Hungarian)

K. 164. Eight points are marked on a circle, at equal distances between adjacent points. Consider all scalene (non-isosceles) triangles formed by the eight points. What may be the angles of the triangle?

(6 points)

Solution (in Hungarian)

K. 165. Billy and Sophie are making rings out of paper strips and link them together to form chains. Each of them uses a 21×30 cm sheet of paper for making the chain. Billy cuts up the sheet parallel to the 21-cm sides, and a Sophie cuts it parallel to the 30-cm sides. Both of them make strips 1 cm wide, curve them into rings and glue them with 0-cm overlaps. The rings link together to form a chain without any deformation. Which chain is longer? (In calculating the perimeter of a circle, use 3.14 for the value of 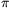$\pi$ , and disregard the thickness of the paper.)

(6 points)

Solution (in Hungarian)

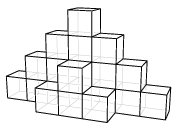
K. 166. Alex is building a pyramid out of congruent cubes, following to the pattern. (He uses no glue, only places the cubes simply next to on top of each other.) Each vertical layer is two cubes taller than the previous one, and forms ascending steps on both sides. When Alex has reached the height of 10 cubes, he goes on decreasing the height of the layers by two cubes in the same fashion. How many cubes does he use altogether?

(6 points)

Solution (in Hungarian)

K. 167. In honour to the Scottish mathematician Dudley Langford, numbers of the following property are called DudLa numbers: Every digit of the number occurs at least twice, and between any pair of identical digits there is as many other digits as the value of the digit in question. For example, 723 121 327 is a DudLa number since there is 1 other digit between two 1's, 2 other digits between two 2's, 3 other digits between two 3's and 7 other digits between two 7's. Find as many 7-digit DudLa numbers as you can.

(6 points)

Solution (in Hungarian)

K. 168. Consider all possible seven-digit numbers formed by using each of the digits 1, 2, 3, 4, 5, 6, 7 once.

a) Show that the difference of any pair of such seven-digit numbers is divisible by 9.

b) How many pairs of different numbers can be selected out of them, such that one is a factor of the other?

(6 points)

Solution (in Hungarian)

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Our web pages are supported by:

ELTE