The hyperbola
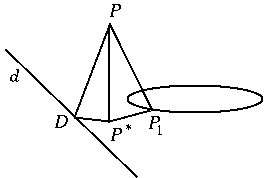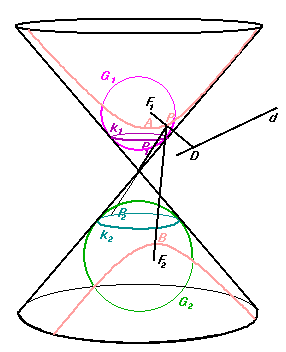
Let P be an arbitrary point of the
conic. Consider the two spheres which touch the cone and the
plane. Let sphere G1 and G2 touch
the cone at circles k1 and k2, and
the plane at points F1 and F2,
respectively. Let the generator through P intersect
k1 and k2 at P1
and P2, respectively. As
PP1=PF1 and
PP2=PF2,
|PF1-PF2|=P1P2.
The line segment P1P2 is bounded
by circles k1 and k2; its length
does not depend on the choice of point P. Hence,
For all points P of the conic,
|PF1-PF2| is constant; and thus,
by the definition, the conic is a hyperbola.
We can prove another important property of the
hyperbola. Let the intersection of the planes of circle
k1 and the hyperbola be line d, and let
D and P* be the projections of P to
d and to the plane of of circle k1,
respectively. It is easy to see that the triangles
PP*P1 are similar for all choices
of P, thus the ratio of distances PP* and
PP1=PF1 is constant. The triangles
PP*D are also similar, which yields that the
ratio of PP* and PD is another
constant. Putting these results together we obtain that
The ratio of the distance of P
from the focus F1 to the distance from the line
d is constant.
The constant is greater than 1, because angle
P*PP1 is the half of the apex
angle of the cone, and angle P*PD is smaller.
Back to the previous page
| 
