 Problem A. 377. (September 2005)
Problem A. 377. (September 2005)
A. 377. The inscribed circle of the triangle ABC touches the side AB at C1, the side BC at A1, and the side CA at B1. It is known that the line segments AA1, BB1 and CC1 pass through a common point. Let N denote that point. Draw the three circles that pass through N and touches two of the sides. Prove that the six points of tangency are concyclic.
(5 pont)
Deadline expired on October 17, 2005.
Solution. Use the notations of the Figure.
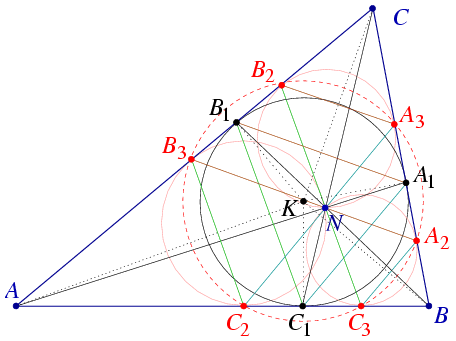
Circle B3C2N can be obtained by scaling the inscribed circle from vertex A. Triangle NB3C2 is the image of triangle A1B1C1, so the sides of these triangles are paralel, respectively. By similar scalings from points B and C we obtain that lines B2N and NC3 are paralel to B1C1. This implies that line B2C3 passes through point N and also this line is paralel to B1C1.
The perpendicular bisector of B1C1 is the angle bisector AK. Since line segments B2C3 and B3C2 are paralel to B1C1, AK is also their perpendicular bisector.
Similarly, the line segments A2B3 and A3B2 share the common perpendicular bisector CK and segments A2C3 and A3C2 share BK.
All these three perpendicular bisectors pass through the incenter K, so KB2=KC3=KA2=KB3=KC2=KA3 and points A2,A3,B2,B3,C2,C3 lie on a certain circle of center K.
Statistics:
23 students sent a solution. 5 points: Erdélyi Márton, Estélyi István, Fischer Richárd, Gyenizse Gergő, Hujter Bálint, Jankó Zsuzsanna, Kisfaludi-Bak Sándor, Kónya 495 Gábor, Korándi Dániel, Kutas Péter, Lovász László Miklós, Molnár 999 András, Nagy 224 Csaba, Paulin Roland, Tomon István, Udvari Balázs, Ureczky Bálint, Viktor Simjanoski. 0 point: 5 students.
Problems in Mathematics of KöMaL, September 2005
