 Problem A. 382. (October 2005)
Problem A. 382. (October 2005)
A. 382. S and T are disjoint sets, * is a binary operation on the elements of S and o is a binary operation on the elements of T. (That is, if a,b S and c,d
S and c,d T, then a*b
T, then a*b S and cod
S and cod T). Each operation is associative. In other words, (S,*) and (T,o) are semigroups. It is also given that for every t
T). Each operation is associative. In other words, (S,*) and (T,o) are semigroups. It is also given that for every t T there are elements u,v
T there are elements u,v T, such that uot=tov=t. Let
T, such that uot=tov=t. Let denote an arbitrary mapping. Define the operation
on the set S
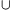 T as follows:
T as follows:
Show that the operation is associative if and only if f is a homomorphism, that is, f(a*b)=f(a)of(b) for all a,b
 S.
S.
Czech competition problem
(5 pont)
Deadline expired on November 15, 2005.
Solution. (a) If f is a homomorphism then is trivially associative.
(b) Suppose that is associative and let a,b be two arbitrary elements of S. By the conditions there exist u,v
 T such that uof(a)=f(a) and f(a*b)ov=f(a*b). Then
T such that uof(a)=f(a) and f(a*b)ov=f(a*b). Then
Statistics:
15 students sent a solution. 5 points: Erdélyi Márton, Estélyi István, Fischer Richárd, Gyenizse Gergő, Hujter Bálint, Jankó Zsuzsanna, Kónya 495 Gábor, Korándi Dániel, Nagy 224 Csaba, Paulin Roland. 4 points: Kisfaludi-Bak Sándor, Tomon István. 2 points: 2 students. 1 point: 1 student.
Problems in Mathematics of KöMaL, October 2005
