 Problem A. 407. (October 2006)
Problem A. 407. (October 2006)
A. 407. In pyramid ABCDE, the angle between plane ACE and faces ABCD, ABE, BCE, CDE and DAE are all 45o. Prove that AB2+AD2=BC2+CD2.
(5 pont)
Deadline expired on November 15, 2006.
Solution. Denote by B' and D' the perpendicular foots of points B and D on plane ACE, respectively. Since the angles between plane ACE and planes ABC, ABE and BCE are all 45o, the distances between B' and lines AC, AE and CE are all equal to BB', independently of the position of B'. Similarly, the distances between D' and lines AC, AE és CE are all equal to DD' (Figure 1).
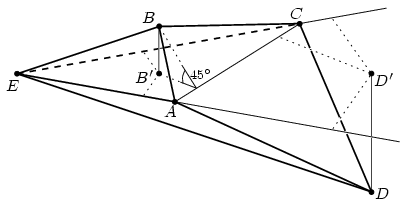
Figure 1.
There exists four such points in the plane of triangle ACE which have equal distances from the three lines AC, AE, CE: the incenter and the three excenters. Denote them by I and, using the usual indexing, by IA, IC and IE, respectively. Points B' and D' are two of these four.
Planes ABE and ADE are symmetric to plane ACE and also planes BCE and CDE are symmetric; this implies that lines BE and DE are symmetric to plane ACE. The perpendicular projections of these two lines coincide. Therefore, points B' and D' lie on the same (interior or exterior) bisector of angle AEC.
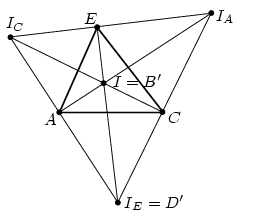
Figure 2.
If B' and D' lie on the interior bisector, then they are I and IE. Due to the symmetry, it can be assumed that B'=I and D'=IE (Figure 2.). From the right triangles ABB', ADD' and AB'D',
AB2+AD2=(AB'2+BB'2)+(AD'2+DD'2)=
=(AB'2+AD'2)+BB'2+DD'2=B'D'2+BB'2+DD'2.
Replacing A by C,
BC2+CD2=(B'C2+BB'2)+(CD'2+DD'2)=
=(B'C2+CD'2)+BB'2+DD'2=B'D'2+BB'2+DD'2.
Therefore AB2+AD2=BC2+CD2, the statement holds.
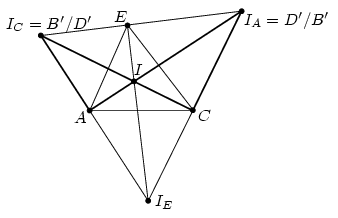
3. ábra
If B' and D' lie on the exterior bisector of angle AEC then they are IA and IC. The quadrilateral AB'CD', which is the projection of face ABCD is sel-intersecting (Figure 3). This case is not possible.
Statistics:
15 students sent a solution. 4 points: Bogár 560 Péter, Bohus Péter, Gyenizse Gergő, Hujter Bálint, Kisfaludi-Bak Sándor, Kónya 495 Gábor, Korándi Dániel, Kornis Kristóf, Lovász László Miklós, Nagy 224 Csaba, Nagy 235 János, Nagy 314 Dániel, Sümegi Károly, Tomon István. 0 point: 1 student.
Problems in Mathematics of KöMaL, October 2006
